ANALYSES TELLi
Cetta page a pour but de présenter un ensemble de méthodes de statistiques (corrélation, ACP, modèle de régression)
HDF-AUV_LIM (min_max)
1 - Analyse des données
Nous cherchons à étudier les liens entre la fréquentation voyageurs 2022 des gares SNCF situées dans les Hauts-de-France (carte 1) et dans les anciennes régions Auvergne et Limousin (carte 2) avec un ensemble de variables quantitatives.
Carte 1 : Cartographie des gares
dans la région des Hauts-de-France 
Carte 2 : Cartographie des
gares des anciennes régions Auvergne et Limousin pacman::p_load(sf, tmap, dplyr, mapview, FactoMineR, factoextra,
performance, # analyser les modèles statistiques
ggplot2, dbscan, broom.helpers, car, factoextra, coorplot
)## Installation du package dans 'C:/Users/oliviertheureaux/AppData/Local/R/win-library/4.5'
## (car 'lib' n'est pas spécifié)## Warning: le package 'coorplot' n'est pas disponible for this version of R
##
## Une version de ce package pour votre version de R est peut-être disponible ailleurs,
## Voyez des idées à
## https://cran.r-project.org/doc/manuals/r-patched/R-admin.html#Installing-packages## Warning: impossible d'accéder à l'index de l'entrepôt http://www.stats.ox.ac.uk/pub/RWin/bin/windows/contrib/4.5:
## impossible d'ouvrir l'URL 'http://www.stats.ox.ac.uk/pub/RWin/bin/windows/contrib/4.5/PACKAGES'## Warning in p_install(package, character.only = TRUE, ...):## Warning in library(package, lib.loc = lib.loc, character.only = TRUE,
## logical.return = TRUE, : aucun package nommé 'coorplot' n'est trouvé## Warning in pacman::p_load(sf, tmap, dplyr, mapview, FactoMineR, factoextra, : Failed to install/load:
## coorplotPour cela nous disposons des variables suivantes. Ces variables ont été calculées pour chaque isochrone de 10 minutes à pied autour de chaque gare.
all_data_hdf <- sf::st_read('processed_data/all_data_region_HDF_foot_10min_20240319_min_max.gpkg') %>%
dplyr::select(-c(ID, reseau_pedestre, pop_p15_2017))## Reading layer `all_data_region_HDF_foot_10min_20240319_min_max' from data source `C:\docs\rprojects\database_sf\processed_data\all_data_region_HDF_foot_10min_20240319_min_max.gpkg'
## using driver `GPKG'
## Simple feature collection with 393 features and 24 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 595141.4 ymin: 6874373 xmax: 781232.5 ymax: 7108435
## Projected CRS: RGF93 v1 / Lambert-93## [1] "ID_number" "voy_2022"
## [3] "sum_population" "sum_population_active"
## [5] "sum_lits" "longueur_route"
## [7] "nb_intersections" "longueur_pistes_cyclables"
## [9] "nombre_arrets" "nombre_parkings"
## [11] "nombre_commerces" "nombre_sante"
## [13] "nombre_loisirs" "nombre_restauration"
## [15] "nombre_sports" "nombre_ronds_points"
## [17] "nombre_eleves" "ZA"
## [19] "passage_niveau" "sum_population_carreau"
## [21] "PNR_OK" "geom"all_data_auv_lim <- sf::st_read('processed_data/all_data_region_Auv_Lim_foot_10min_20240319_min_max.gpkg')## Reading layer `all_data_region_Auv_Lim_foot_10min_20240319_min_max' from data source `C:\docs\rprojects\database_sf\processed_data\all_data_region_Auv_Lim_foot_10min_20240319_min_max.gpkg'
## using driver `GPKG'
## Simple feature collection with 209 features and 21 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 530264.7 ymin: 6401103 xmax: 805938 ymax: 6617711
## Projected CRS: RGF93 v1 / Lambert-93## [1] "ID_number" "voy_2022"
## [3] "sum_population" "sum_population_active"
## [5] "sum_lits" "longueur_route"
## [7] "nb_intersections" "longueur_pistes_cyclables"
## [9] "nombre_arrets" "nombre_parkings"
## [11] "nombre_commerces" "nombre_sante"
## [13] "nombre_loisirs" "nombre_restauration"
## [15] "nombre_sports" "nombre_ronds_points"
## [17] "nombre_eleves" "ZA"
## [19] "passage_niveau" "sum_population_carreau"
## [21] "PNR_OK" "geom"Nombre de voyageurs total
## [1] 124037704Top 10 des gares
## Simple feature collection with 10 features and 2 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 650564.5 ymin: 6519931 xmax: 736844.4 ymax: 7060255
## Projected CRS: RGF93 v1 / Lambert-93
## nom_gare voy_2022 geom
## 1 Lille Flandres 21992946 POINT (704951.3 7059959)
## 2 Lille Europe 6056899 POINT (705371 7060255)
## 3 Amiens 6004673 POINT (650564.5 6977107)
## 4 Creil 5224702 POINT (661361.1 6907253)
## 5 Clermont Ferrand 4095262 POINT (707812.6 6519931)
## 6 Arras 3920113 POINT (684439.8 7020999)
## 7 Douai 2964246 POINT (706410.5 7030449)
## 8 Valenciennes 2875726 POINT (736844.4 7029628)
## 9 Chantilly-Gouvieux 2600290 POINT (660614.6 6898746)
## 10 Compiègne 2341622 POINT (687203.1 6924742)## Rows: 602
## Columns: 22
## $ ID_number <chr> "Pont de la Deûle", "Outreau", "Sous le Bois…
## $ voy_2022 <dbl> 24168, 0, 8, 554, 513226, 1989, 238, 3920113…
## $ sum_population <dbl> 0.1751477517, 0.0601894551, 0.1192634891, 0.…
## $ sum_population_active <dbl> 0.1507132358, 0.0541060553, 0.0942287243, 0.…
## $ sum_lits <dbl> 0.0329117367, 0.0072079423, 0.0425676595, 0.…
## $ longueur_route <dbl> 0.343967986, 0.006168987, 0.296963409, 0.219…
## $ nb_intersections <dbl> 0.27310924, 0.00000000, 0.25315126, 0.228991…
## $ longueur_pistes_cyclables <dbl> 0.036460243, 0.000000000, 0.000000000, 0.057…
## $ nombre_arrets <dbl> 0.088000000, 0.000000000, 0.005333333, 0.005…
## $ nombre_parkings <dbl> 0.0001071123, 0.0000000000, 0.0002142245, 0.…
## $ nombre_commerces <dbl> 0.004201681, 0.000000000, 0.018907563, 0.000…
## $ nombre_sante <dbl> 0.106796117, 0.000000000, 0.009708738, 0.000…
## $ nombre_loisirs <dbl> 0.01176471, 0.00000000, 0.03529412, 0.000000…
## $ nombre_restauration <dbl> 0.007984032, 0.000000000, 0.013972056, 0.001…
## $ nombre_sports <dbl> 0.00000000, 0.00000000, 0.00000000, 0.000000…
## $ nombre_ronds_points <dbl> 0.2, 0.0, 0.1, 0.2, 0.6, 0.3, 0.0, 0.2, 0.0,…
## $ nombre_eleves <dbl> 0.0000000, 0.0000000, 0.0000000, 0.0000000, …
## $ ZA <dbl> 0.3966329, 0.1188995, 0.4081313, 0.3235975, …
## $ passage_niveau <dbl> 0.1666667, 0.0000000, 0.0000000, 0.0000000, …
## $ sum_population_carreau <dbl> 0.2364492977, 0.0098190304, 0.1871339879, 0.…
## $ PNR_OK <dbl> 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0,…
## $ geom <POINT [m]> POINT (706054.2 7033395), POINT (60171…
Boxplots des données
data_all_boxplot <- all_data %>%
dplyr::select(sum_population, sum_population_active, sum_lits, longueur_route,
nb_intersections, longueur_pistes_cyclables,
nombre_arrets,nombre_parkings, nombre_commerces,nombre_sante,
nombre_loisirs, nombre_restauration, nombre_sports,
nombre_ronds_points, nombre_eleves, ZA, passage_niveau,
sum_population_carreau, PNR_OK) %>%
st_drop_geometry()boxplot(data_all_boxplot, main = "Données HDF 10 min à pied",
las = 2) # Rotate labels by 90 degrees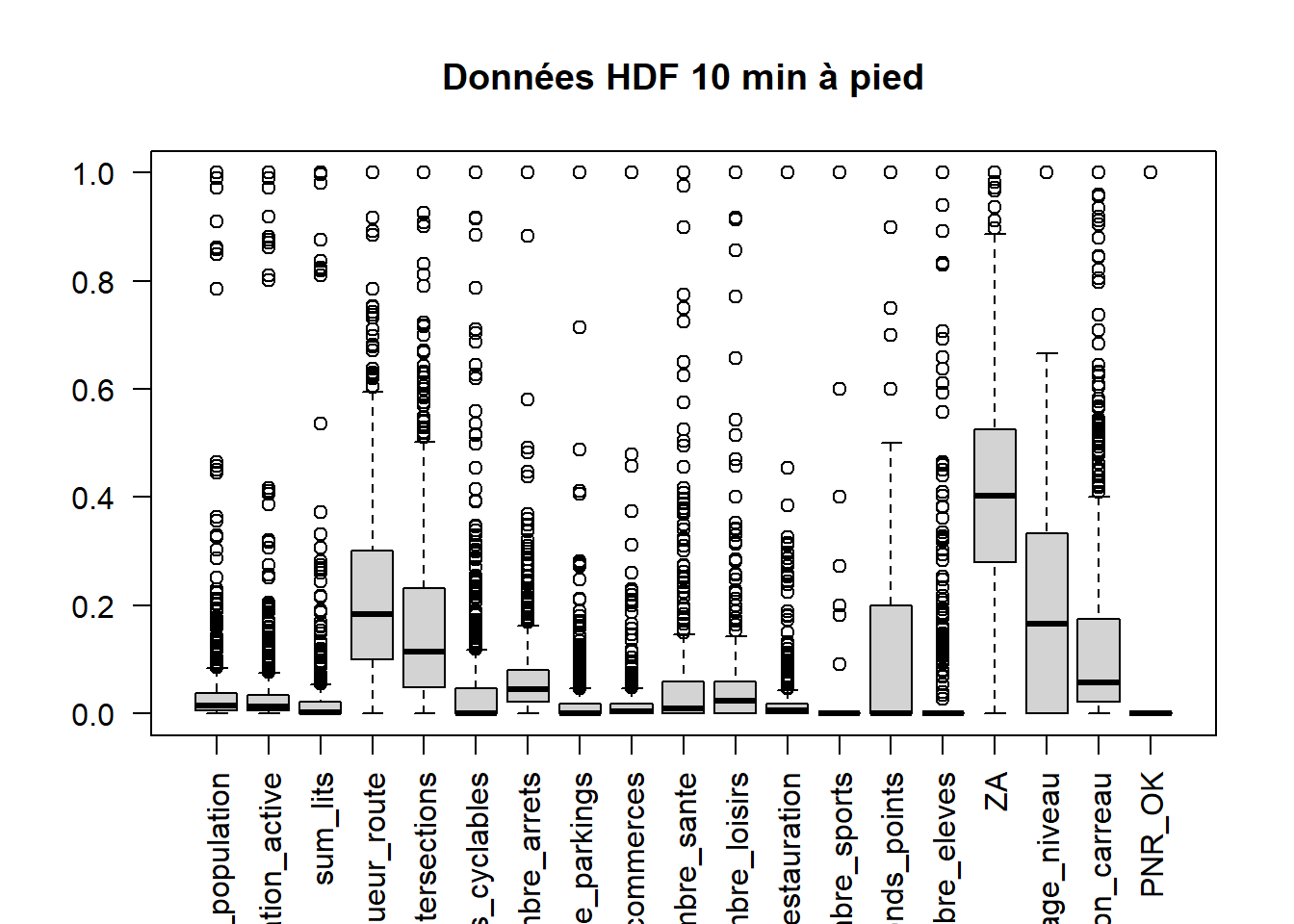
Distribution de la variable dépendante
hist(all_data$voy_2022,
freq=T,
breaks = 100,
col = "darkblue",
border = "white",
main = "Voyageurs 2022 Hauts-de-France")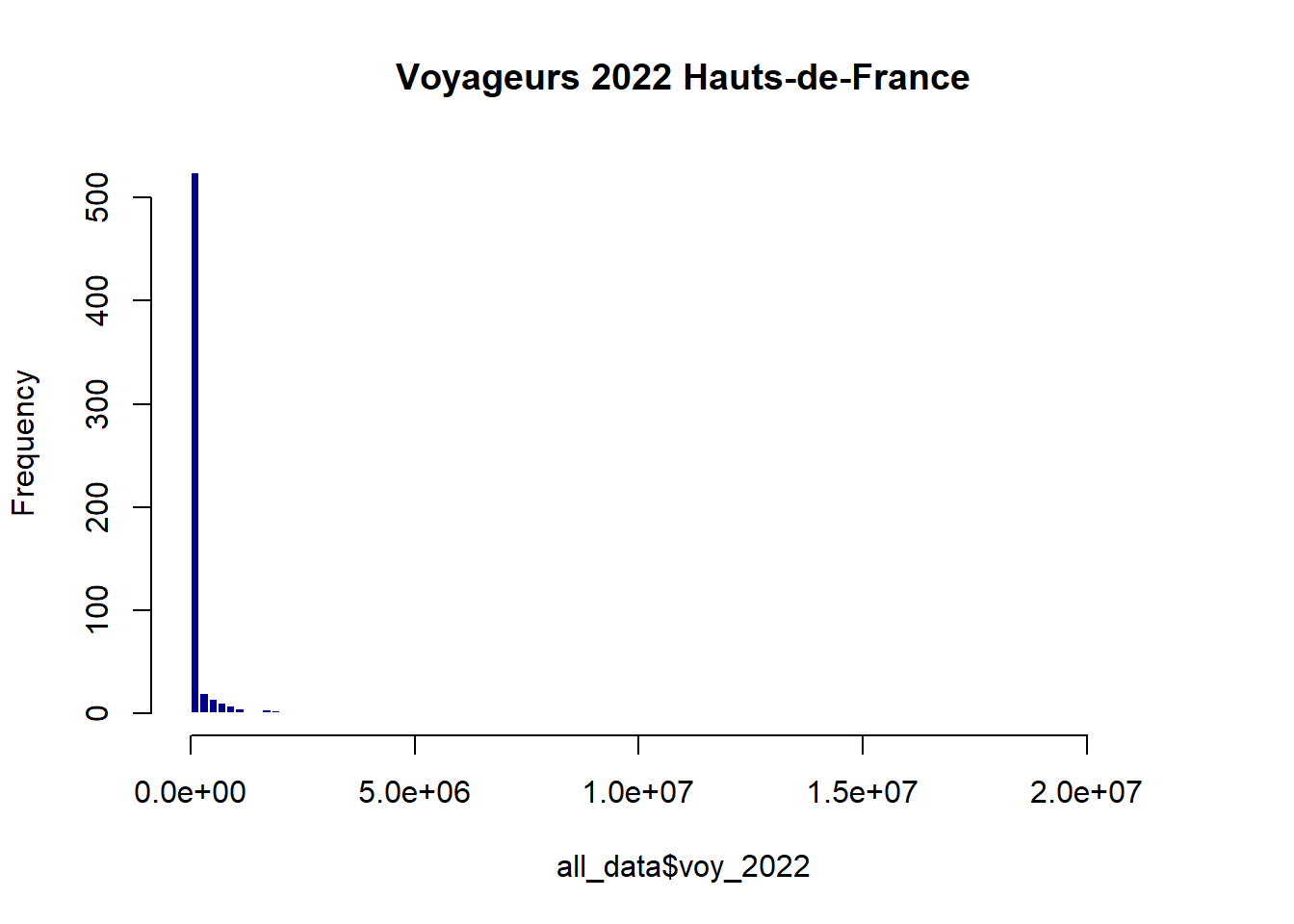
Détection des outliers avec DBScan
library(dbscan) dbscan_result <- dbscan(all_data, eps = 5, minPts = 8) dbscan_result
Suppression des valeurs aberrantes: gares >= à 10 voyageurs par an et inf à 10 000 000
Appliquer une transformation logarithmique à la variable dépendante
Transformation logarithmique : Elle est particulièrement utile pour les données qui suivent une distribution exponentielle ou log-normale. La transformation peut aider à stabiliser la variance des résidus et à rendre les relations entre les variables plus linéaires, ce qui est souhaitable dans la régression linéaire.
Distribution de la variable dépendante transformée
hist(all_data_filter$log_voy_2022,
freq=T,
breaks = 100,
col = "darkblue",
border = "white",
main = "Voyageurs 2022 Hauts-de-France")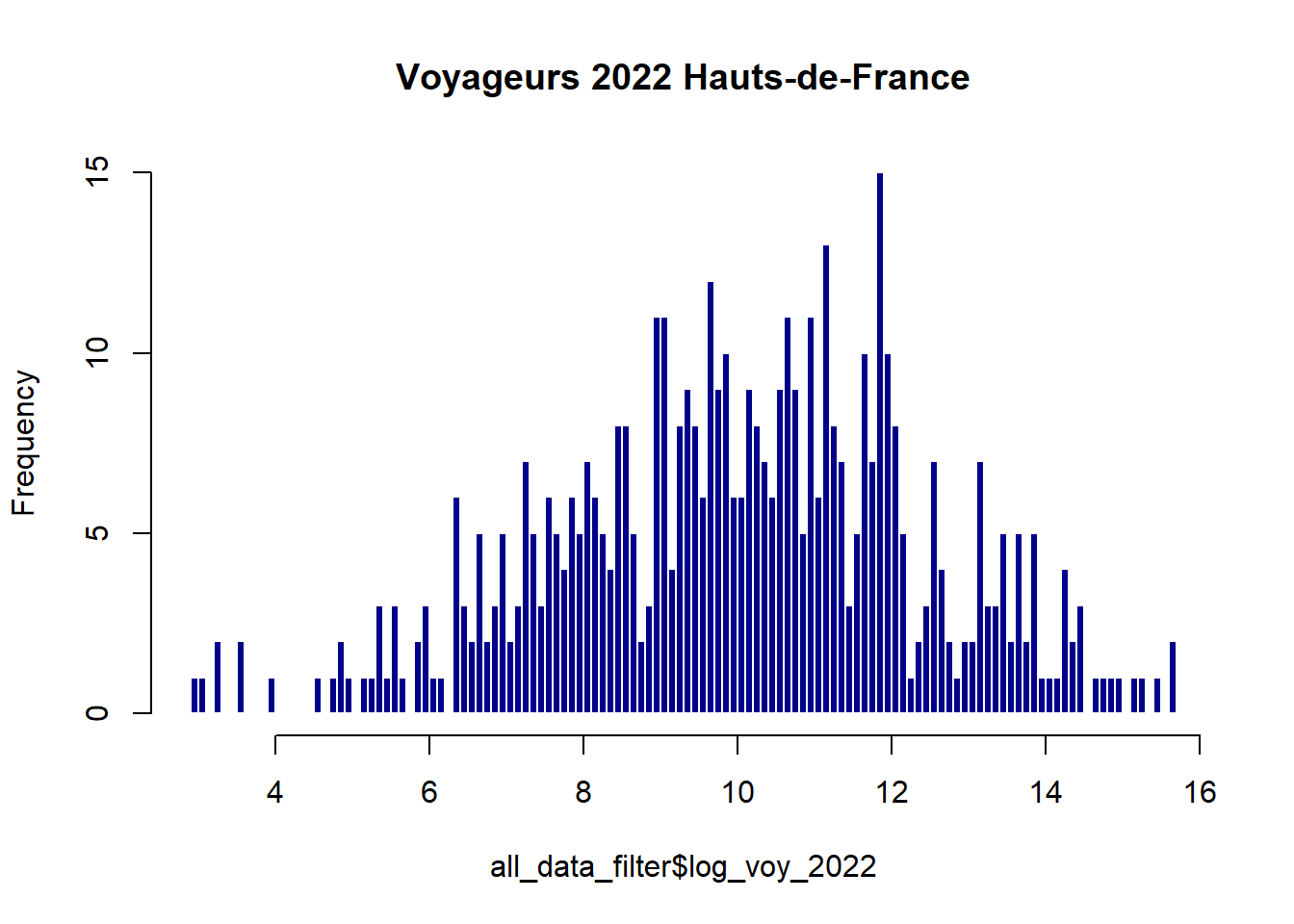
Normalité de la variable dépendante
La variable dépendante voy_2020 suit bien une loi normale (p_value > 0.05)
##
## Shapiro-Wilk normality test
##
## data: all_data_filter$log_voy_2022
## W = 0.9941, p-value = 0.05065Matrice de corrélation
data_for_cor <-
all_data_filter[, c(
"log_voy_2022",
"sum_population",
"sum_population_active",
"sum_lits",
"longueur_route",
"nb_intersections",
# "reseau_pedestre" ,
"longueur_pistes_cyclables",
"nombre_arrets",
"nombre_parkings",
"nombre_commerces",
"nombre_sante",
"nombre_loisirs",
"nombre_restauration",
"nombre_sports",
"nombre_ronds_points",
"nombre_eleves",
"ZA",
"passage_niveau",
"sum_population_carreau",
"PNR_OK"
)]
data_for_cor <- sf::st_drop_geometry(data_for_cor)
mcor <- cor(data_for_cor, use = "complete.obs")
corrplot::corrplot(mcor,
type="upper",
order="hclust",
tl.col="black")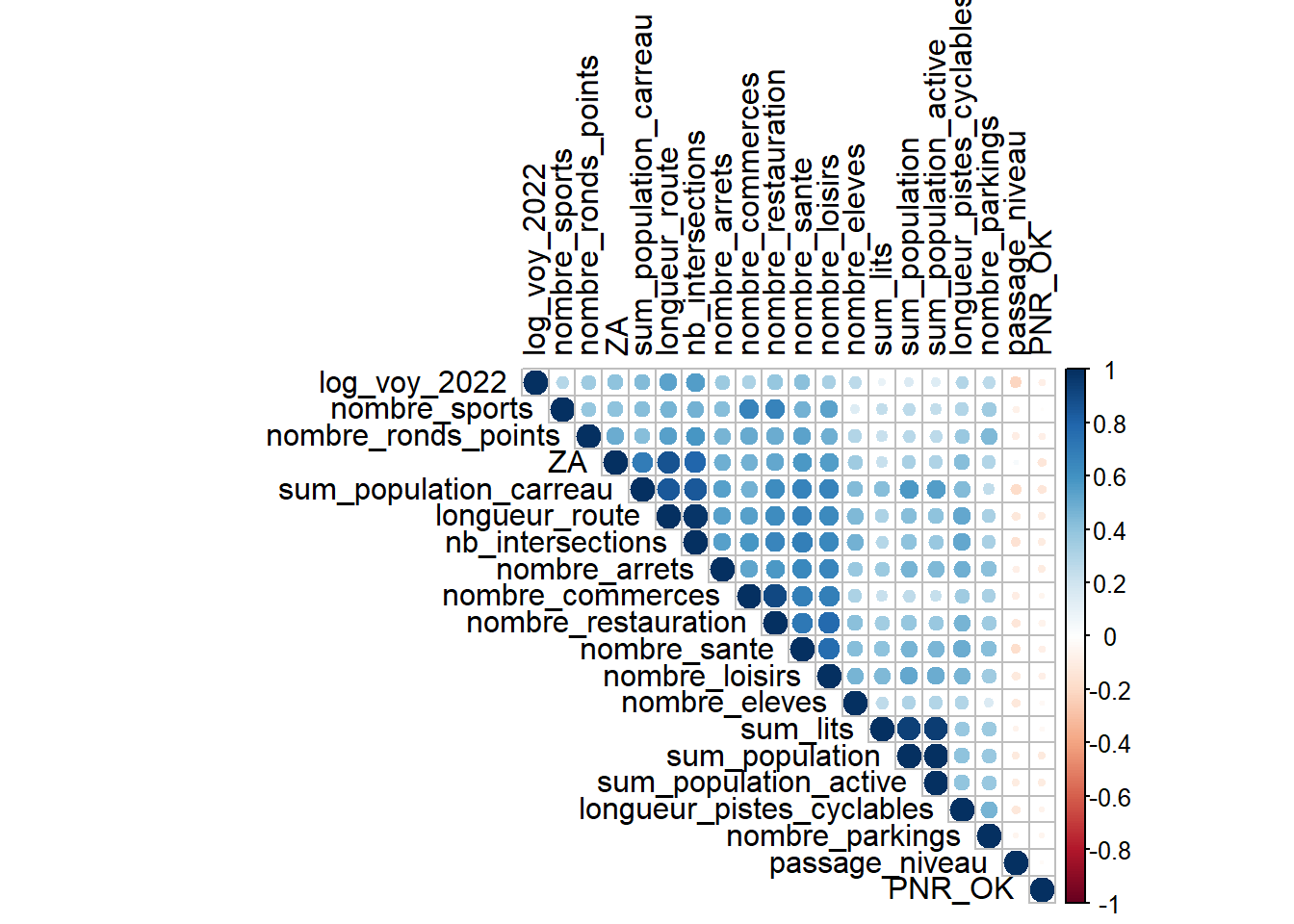
2 - Analyse en composantes principales (ACP)
L’analyse en composantes principales crée de nouvelles variables :
des facteurs ou des composantes. Les facteurs sont des combinaisons
linéaires des variables introduites. On cherche à réduire le nombre de
variables en ne conservant qu’une ou deux variables (composantes)
regroupant la variation la plus importante de l’ensemble des variables
introduites.
Les variables de chaque composante sont fortement corrélées.
En ne conservant que les variables les plus importantes de chaque
composante, on ne perd pas d’information mais on réduit le nombre de
variables.
## Rows: 498
## Columns: 23
## $ ID_number <chr> "Pont de la Deûle", "Les Bons-Pères", "Maube…
## $ voy_2022 <dbl> 24168, 554, 513226, 1989, 238, 3920113, 1494…
## $ sum_population <dbl> 0.1751477517, 0.0189921255, 0.1192634891, 0.…
## $ sum_population_active <dbl> 0.1507132358, 0.0174699951, 0.0942287243, 0.…
## $ sum_lits <dbl> 0.0329117367, 0.0000000000, 0.0425676595, 0.…
## $ longueur_route <dbl> 0.34396799, 0.21975495, 0.50399247, 0.296212…
## $ nb_intersections <dbl> 0.27310924, 0.22899160, 0.51995798, 0.279411…
## $ longueur_pistes_cyclables <dbl> 0.036460243, 0.057294562, 0.080591151, 0.000…
## $ nombre_arrets <dbl> 0.088000000, 0.005333333, 0.026666667, 0.064…
## $ nombre_parkings <dbl> 0.0001071123, 0.0000000000, 0.0502356470, 0.…
## $ nombre_commerces <dbl> 0.004201681, 0.000000000, 0.031512605, 0.008…
## $ nombre_sante <dbl> 0.106796117, 0.000000000, 0.019417476, 0.019…
## $ nombre_loisirs <dbl> 0.01176471, 0.00000000, 0.02352941, 0.047058…
## $ nombre_restauration <dbl> 0.007984032, 0.001996008, 0.059880240, 0.005…
## $ nombre_sports <dbl> 0.00000000, 0.00000000, 0.09090909, 0.000000…
## $ nombre_ronds_points <dbl> 0.2, 0.2, 0.6, 0.3, 0.0, 0.2, 0.0, 0.0, 0.2,…
## $ nombre_eleves <dbl> 0.0000000, 0.0000000, 0.0000000, 0.1255887, …
## $ ZA <dbl> 0.3966329, 0.3235975, 0.4251031, 0.5001756, …
## $ passage_niveau <dbl> 0.1666667, 0.0000000, 0.0000000, 0.6666667, …
## $ sum_population_carreau <dbl> 0.2364492977, 0.0875346748, 0.1503236317, 0.…
## $ PNR_OK <dbl> 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ geom <POINT [m]> POINT (706054.2 7033395), POINT (77214…
## $ log_voy_2022 <dbl> 10.092785, 6.317165, 13.148472, 7.595387, 5.…data_select <- all_data_filter %>%
select(sum_population,
sum_population_active,
sum_lits,
longueur_route,
nb_intersections,
# reseau_pedestre,
longueur_pistes_cyclables,
nombre_arrets,
nombre_parkings,
nombre_commerces,
nombre_sante,
nombre_loisirs,
nombre_restauration,
nombre_sports,
nombre_ronds_points,
nombre_eleves,
ZA,
passage_niveau,
sum_population_carreau,
PNR_OK
) %>%
sf::st_drop_geometry()# Coefficient de corrélation de PEARSON
# Ces coefficients mesurent la force et la direction de la relation linéaire entre chaque paire de variables
stats::cor(data_select, use = "complete.obs")# Lancement de l'ACP
PCA <- FactoMineR::PCA(data_select,
quanti.sup = c(),
quali.sup = c("PNR_OK"), # valeur binaire traitée comme une variable supplémentaire
scale.unit = T) # normalisation des variables## Warning: ggrepel: 5 unlabeled data points (too many overlaps). Consider
## increasing max.overlaps## Warning in geom_bar(stat = "identity", fill = barfill, color = barcolor, :
## Ignoring empty aesthetic: `width`.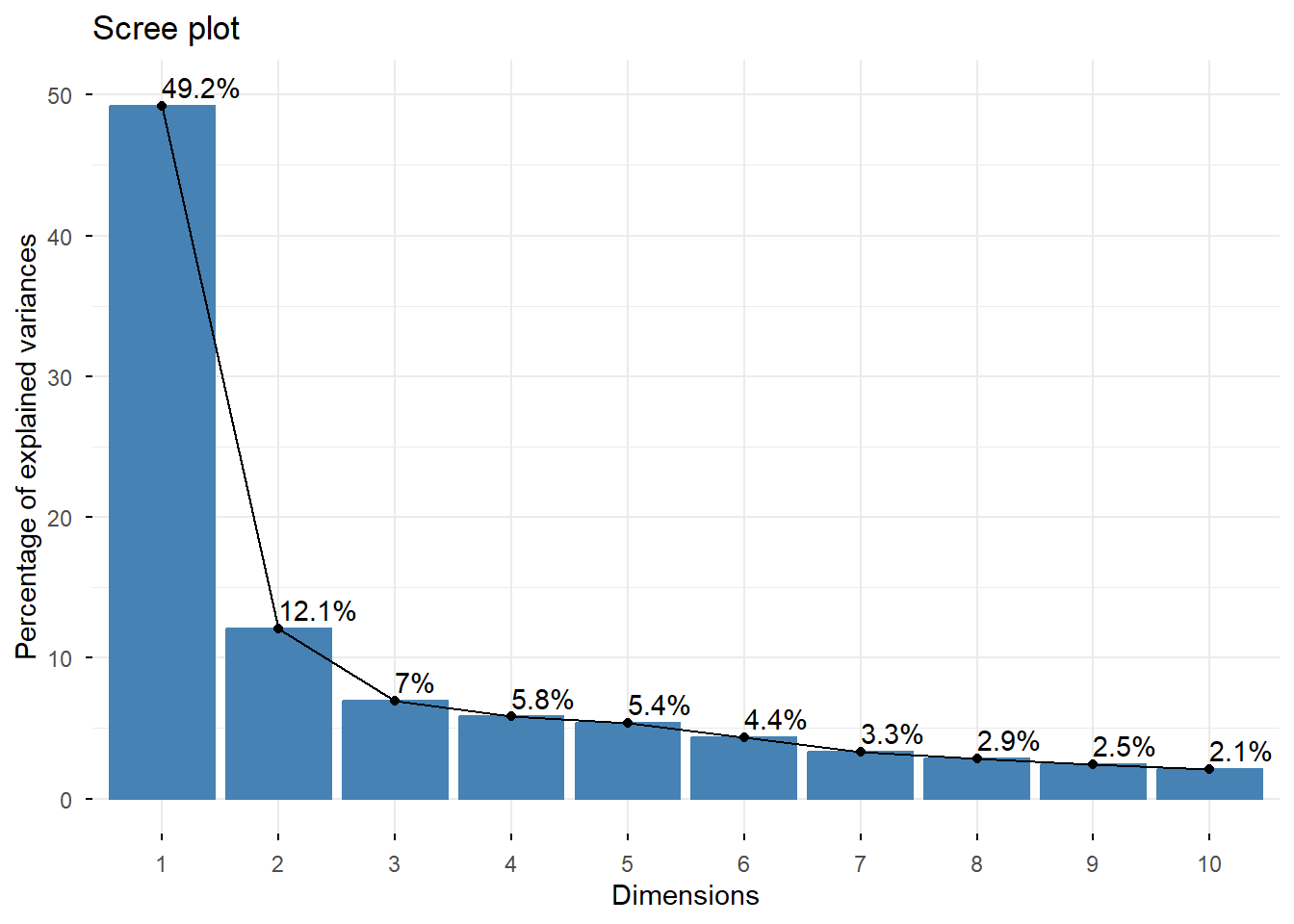
# Cercle des corrélations
factoextra::fviz_pca_var(PCA, col.var="contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## ℹ The deprecated feature was likely used in the ggpubr package.
## Please report the issue at <https://github.com/kassambara/ggpubr/issues>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.## Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
## ℹ Please use tidy evaluation idioms with `aes()`.
## ℹ See also `vignette("ggplot2-in-packages")` for more information.
## ℹ The deprecated feature was likely used in the factoextra package.
## Please report the issue at <https://github.com/kassambara/factoextra/issues>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.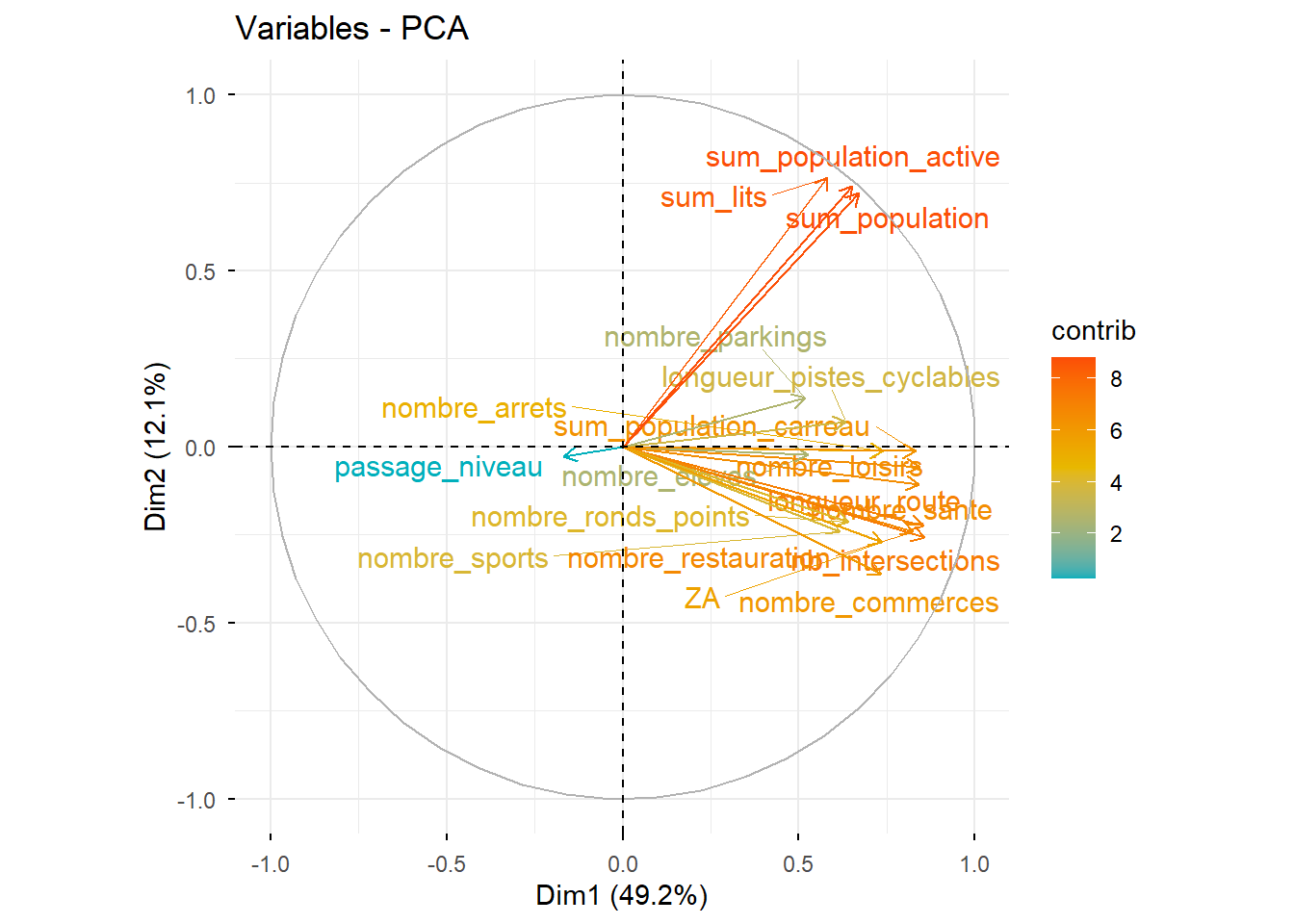
# Graphique des individus
factoextra::fviz_pca_ind(PCA, col.ind = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)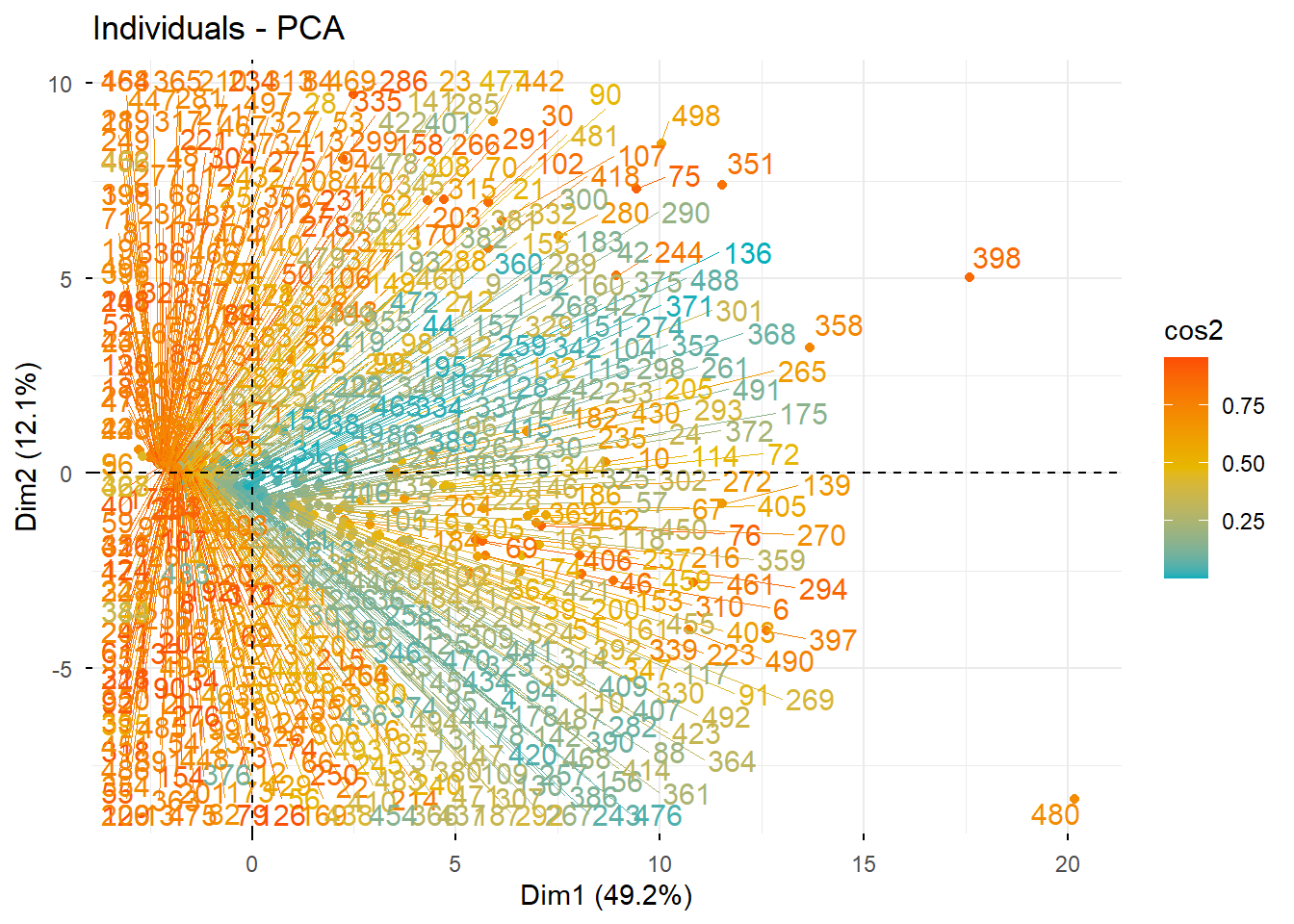
## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 8.8559422411 49.19967912 49.19968
## comp 2 2.1720576319 12.06698684 61.26667
## comp 3 1.2543056661 6.96836481 68.23503
## comp 4 1.0487421884 5.82634549 74.06138
## comp 5 0.9687201918 5.38177884 79.44316
## comp 6 0.7871156908 4.37286495 83.81602
## comp 7 0.6008773341 3.33820741 87.15423
## comp 8 0.5148327296 2.86018183 90.01441
## comp 9 0.4424071786 2.45781766 92.47223
## comp 10 0.3817408373 2.12078243 94.59301
## comp 11 0.2605800218 1.44766679 96.04068
## comp 12 0.2365785625 1.31432535 97.35500
## comp 13 0.2192855151 1.21825286 98.57325
## comp 14 0.1254877157 0.69715398 99.27041
## comp 15 0.0678815424 0.37711968 99.64753
## comp 16 0.0482203956 0.26789109 99.91542
## comp 17 0.0144787432 0.08043746 99.99586
## comp 18 0.0007458138 0.00414341 100.00000# Contribution de chaque variable aux deux premiers axes
factoextra::fviz_contrib(PCA, choice = "var", axes = 1) # axe 1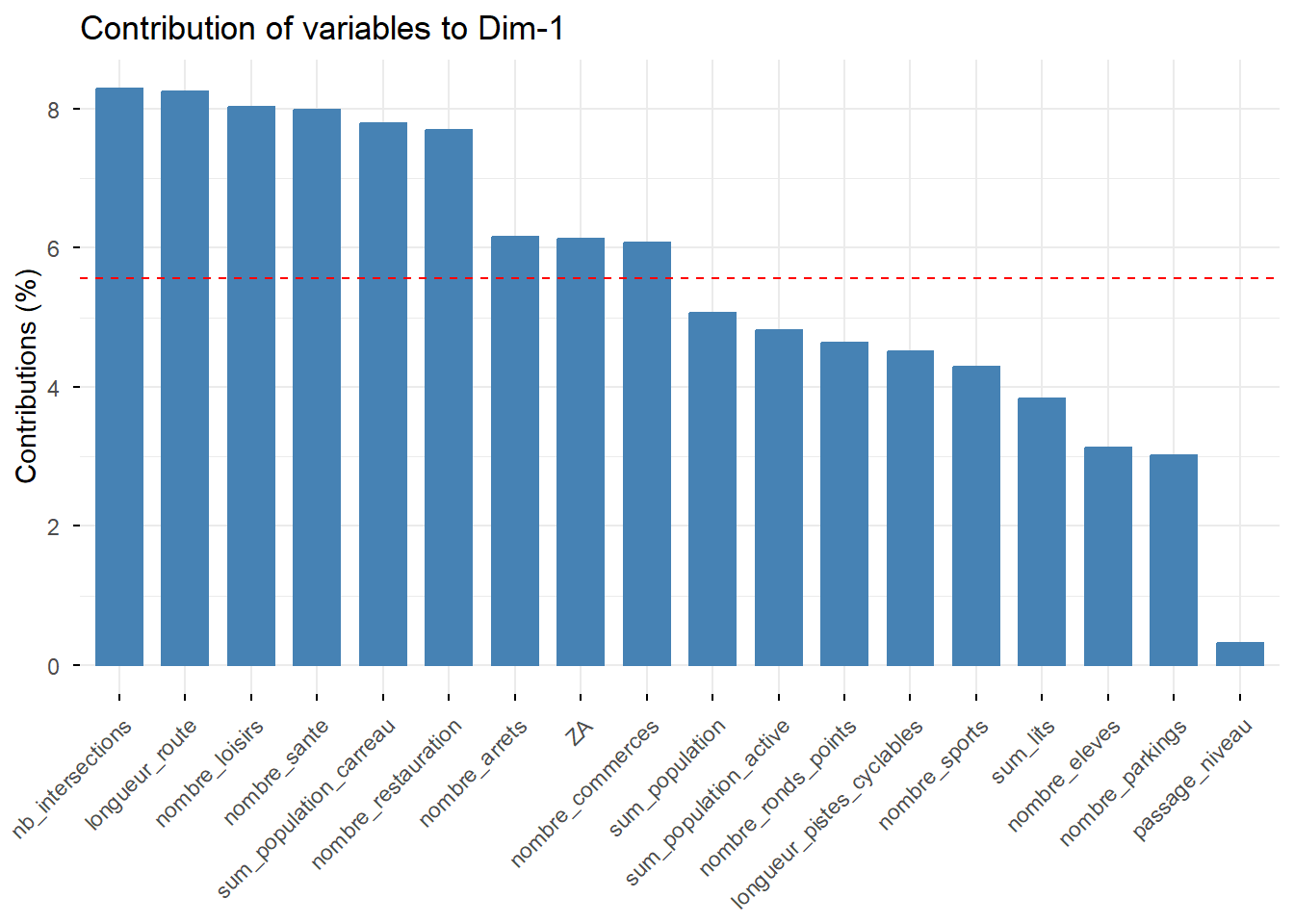
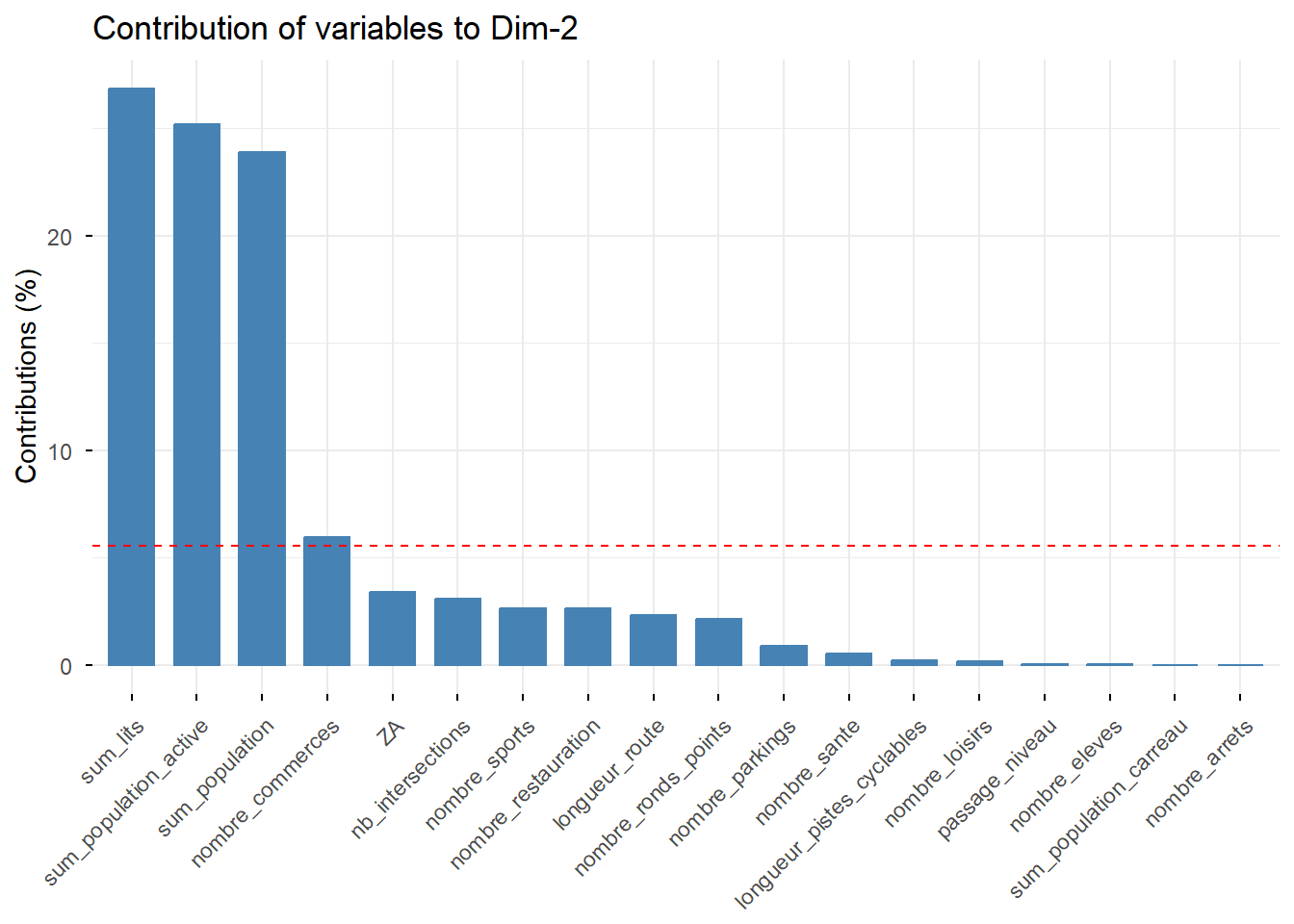
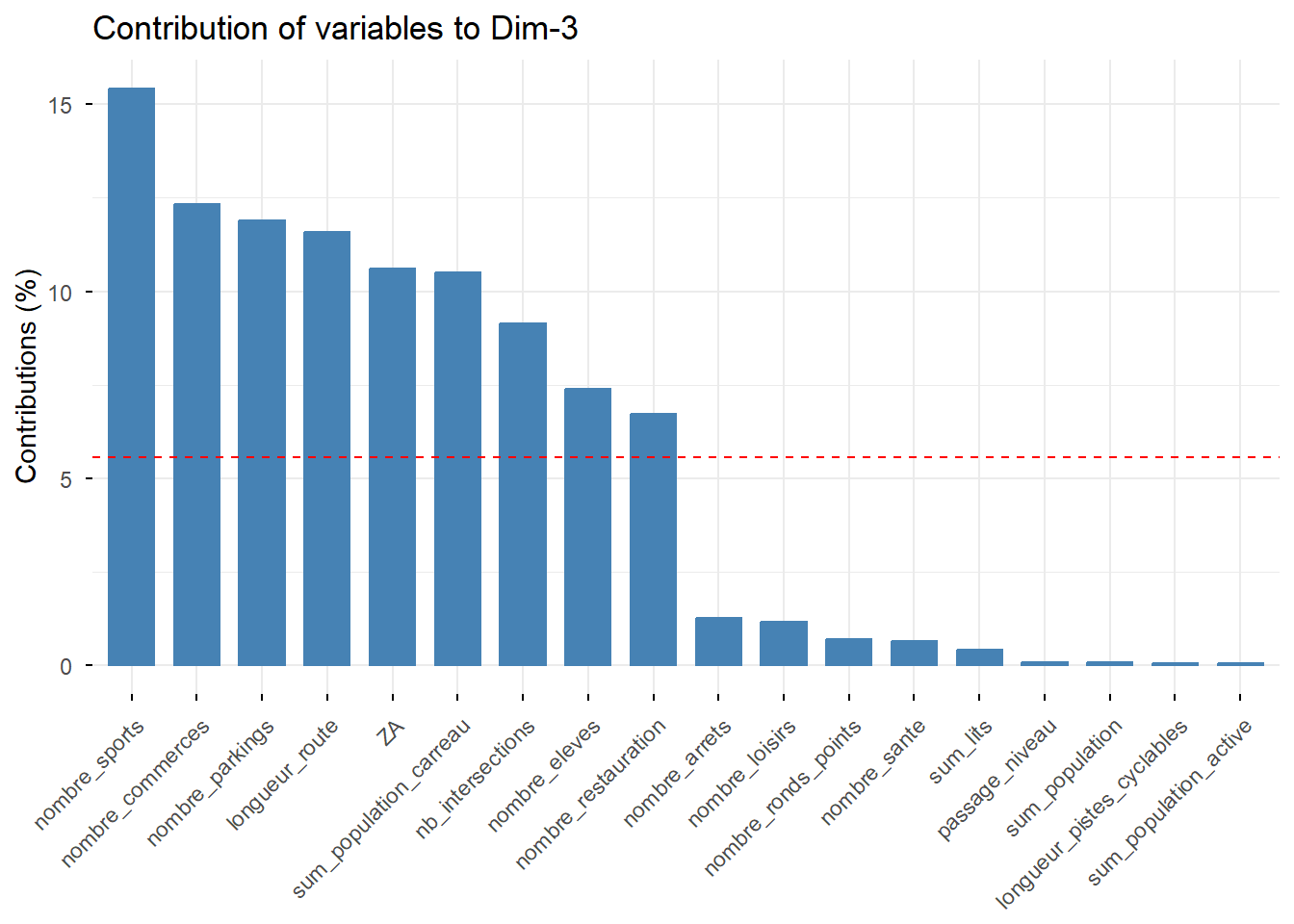
3 - Classification ascendante hiérarchique et cartographie
# CAH sur les scores des individus de l'ACP ----
hc <- HCPC(PCA, nb.clust = 3, graph = FALSE)
# Visualiser les dendrogrammes
fviz_dend(hc, cex = 0.5)## Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as
## of ggplot2 3.3.4.
## ℹ The deprecated feature was likely used in the factoextra package.
## Please report the issue at <https://github.com/kassambara/factoextra/issues>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.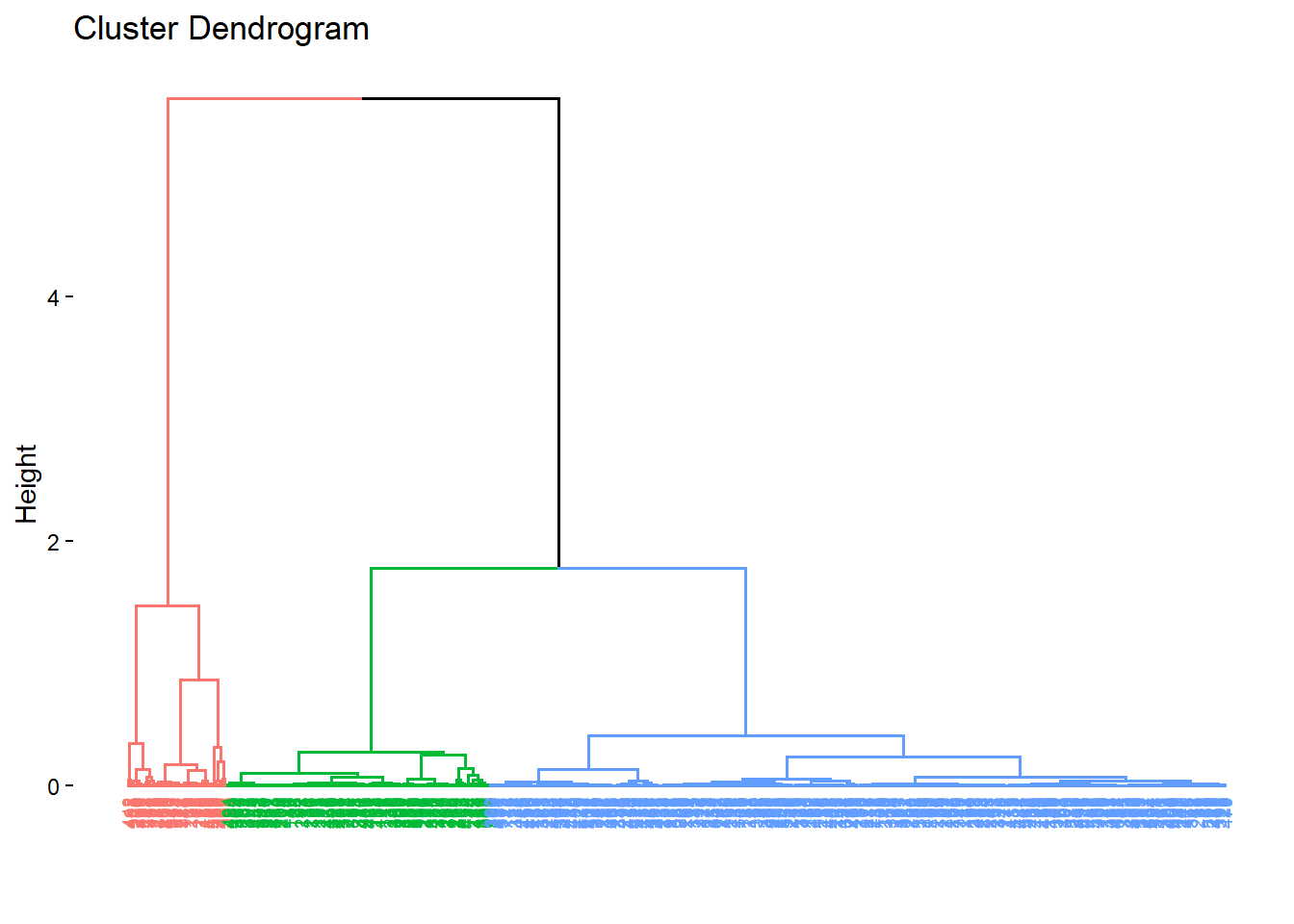
# Visualiser les individus dans le plan factoriel avec une indication de leur cluster
fviz_cluster(hc, geom = "point")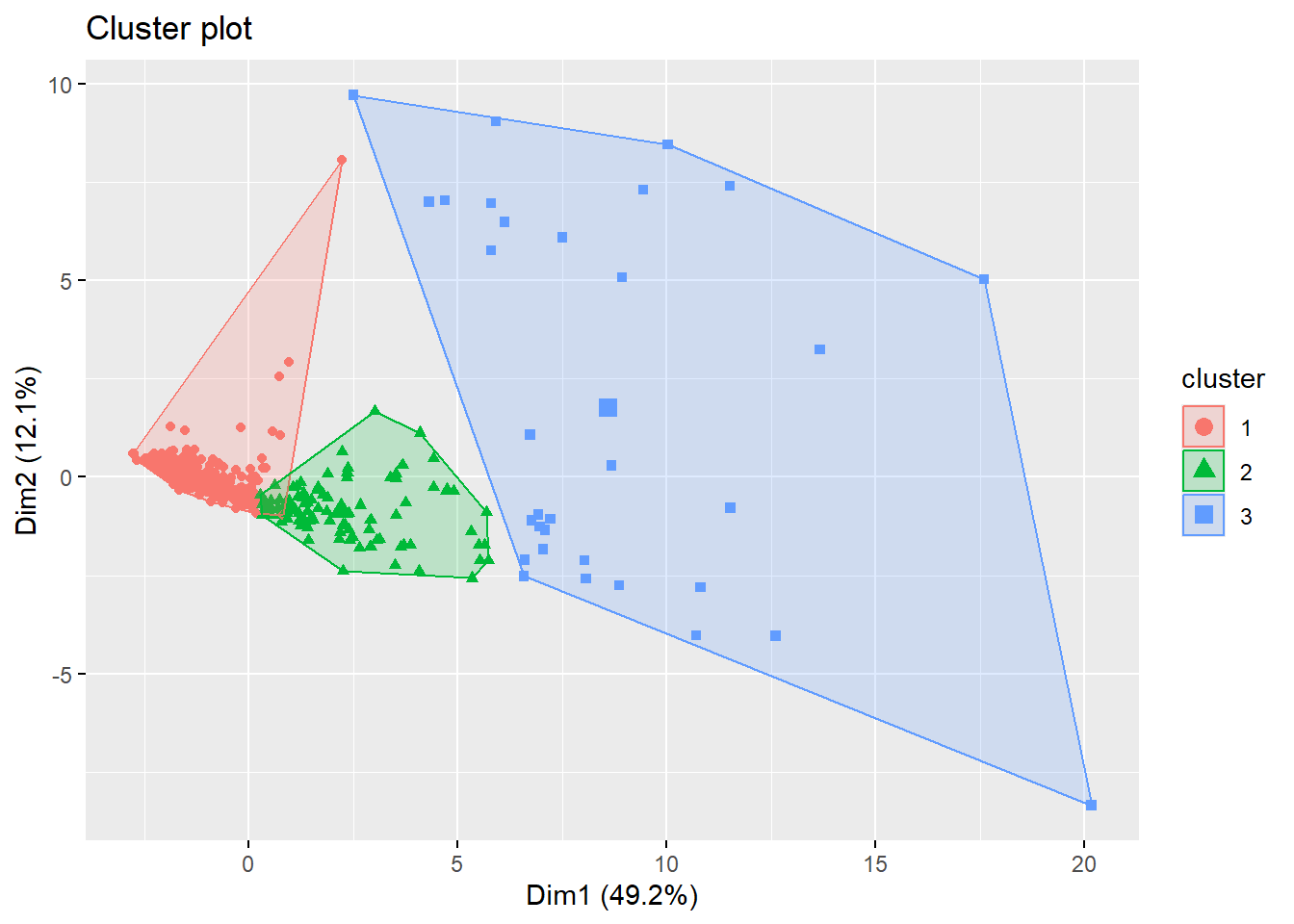
# Extraction des clusters attribués à chaque observation
clusters <- hc$data.clust$clust
length(clusters)## [1] 498## [1] 498## ℹ tmap modes "plot" - "view"
## ℹ toggle with `tmap::ttm()`tm_shape(all_data_filter) +
tm_dots(col = "cluster", palette = "Set1", title = "Cluster") +
tm_basemap(server = "OpenStreetMap") +
tm_layout(legend.position = c("left", "bottom"))##
## ── tmap v3 code detected ───────────────────────────────────────────────────────
## [v3->v4] `tm_tm_dots()`: migrate the argument(s) related to the scale of the
## visual variable `fill` namely 'palette' (rename to 'values') to fill.scale =
## tm_scale(<HERE>).[v3->v4] `tm_dots()`: use 'fill' for the fill color of polygons/symbols
## (instead of 'col'), and 'col' for the outlines (instead of 'border.col').[tm_dots()] Argument `title` unknown.[cols4all] color palettes: use palettes from the R package cols4all. Run
## `cols4all::c4a_gui()` to explore them. The old palette name "Set1" is named
## "brewer.set1"4 - Construction du modèle de régression linéaire
modele <- lm(
log_voy_2022 ~
sum_population+
sum_population_active+
sum_lits+
longueur_route+
nb_intersections+
# reseau_pedestre+
longueur_pistes_cyclables+
nombre_arrets+
nombre_parkings+
nombre_commerces+
nombre_sante+
nombre_loisirs+
nombre_restauration+
nombre_sports+
nombre_ronds_points+
nombre_eleves+
ZA+
passage_niveau+
sum_population_carreau+
PNR_OK,
data = all_data_filter
)
# Affichage du résumé du modèle pour voir les coefficients et la significativité des variables
summary(modele)##
## Call:
## lm(formula = log_voy_2022 ~ sum_population + sum_population_active +
## sum_lits + longueur_route + nb_intersections + longueur_pistes_cyclables +
## nombre_arrets + nombre_parkings + nombre_commerces + nombre_sante +
## nombre_loisirs + nombre_restauration + nombre_sports + nombre_ronds_points +
## nombre_eleves + ZA + passage_niveau + sum_population_carreau +
## PNR_OK, data = all_data_filter)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.7953 -1.0824 0.2544 1.4071 4.2212
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.1128 0.2753 33.100 < 2e-16 ***
## sum_population -33.6971 13.0266 -2.587 0.009982 **
## sum_population_active 34.3243 14.2528 2.408 0.016407 *
## sum_lits -3.0694 2.3288 -1.318 0.188125
## longueur_route 7.6569 3.0980 2.472 0.013801 *
## nb_intersections 2.8346 2.5832 1.097 0.273038
## longueur_pistes_cyclables -1.4785 0.8027 -1.842 0.066086 .
## nombre_arrets 3.3874 1.2065 2.808 0.005194 **
## nombre_parkings 2.9267 1.2152 2.408 0.016397 *
## nombre_commerces -10.5301 3.3302 -3.162 0.001666 **
## nombre_sante 1.7594 1.1896 1.479 0.139812
## nombre_loisirs -2.6050 1.2568 -2.073 0.038729 *
## nombre_restauration 12.4867 3.6410 3.430 0.000657 ***
## nombre_sports 0.6074 1.5054 0.404 0.686760
## nombre_ronds_points 0.1827 0.6419 0.285 0.776063
## nombre_eleves 0.1439 0.7051 0.204 0.838351
## ZA -2.6464 1.1695 -2.263 0.024099 *
## passage_niveau -1.6457 0.5078 -3.241 0.001274 **
## sum_population_carreau -1.6280 1.1014 -1.478 0.140040
## PNR_OK -0.2293 0.2593 -0.885 0.376870
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.899 on 478 degrees of freedom
## Multiple R-squared: 0.3877, Adjusted R-squared: 0.3633
## F-statistic: 15.93 on 19 and 478 DF, p-value: < 2.2e-16Coefficient de détermination
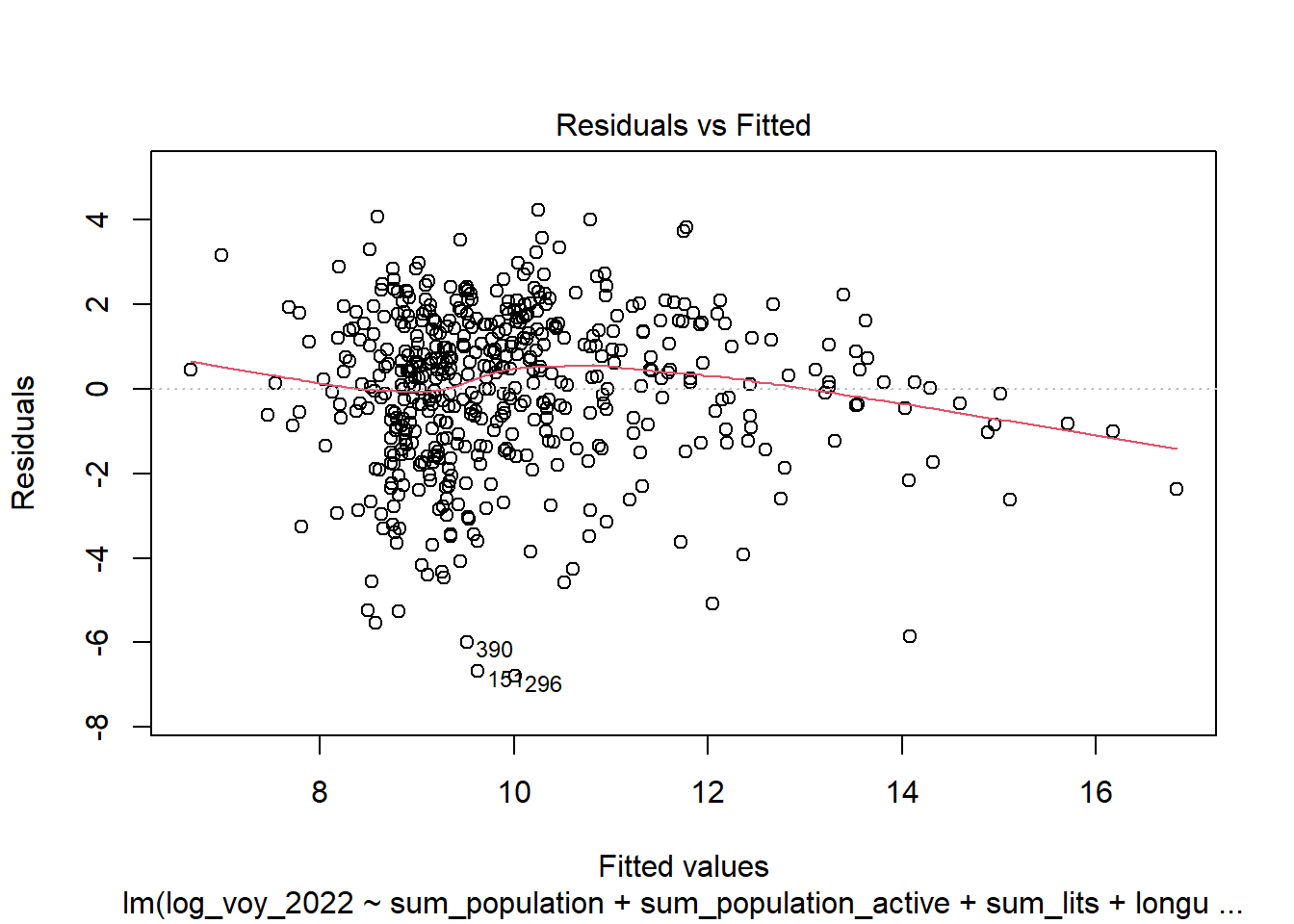
## [1] 0.3876705Diagnostic visuel des résidus
Quatre graphiques de diagnostic résiduels pour aider à évaluer la qualité de l’ajustement du modèle. Ces graphiques fournissent des informations visuelles sur divers aspects des résidus et des ajustements du modèle :
Observation des linéarités des relations : Résidus vs Valeurs Prédites : Ce graphique montre les résidus (différences entre les valeurs observées et les valeurs prédites) en fonction des valeurs prédites par le modèle. L’idéal est de voir une dispersion aléatoire des points autour de la ligne horizontale à zéro, indiquant l’homoscédasticité (variance constante des résidus). Des motifs ou des tendances dans ce graphique peuvent indiquer des problèmes d’hétéroscédasticité ou des non-linéarités non capturées par le modèle.
Normalité des résidus : Q-Q Plot des Résidus Standardisés : Ce graphique compare la distribution des résidus standardisés à une distribution normale théorique. Si les résidus sont normalement distribués, les points devraient approximativement suivre la ligne diagonale. Des écarts significatifs de cette ligne peuvent indiquer une violation de l’hypothèse de normalité des résidus, ce qui peut affecter les tests d’hypothèse et les intervalles de confiance associés au modèle. (Voir aussi test de Shapiro-Wilk)
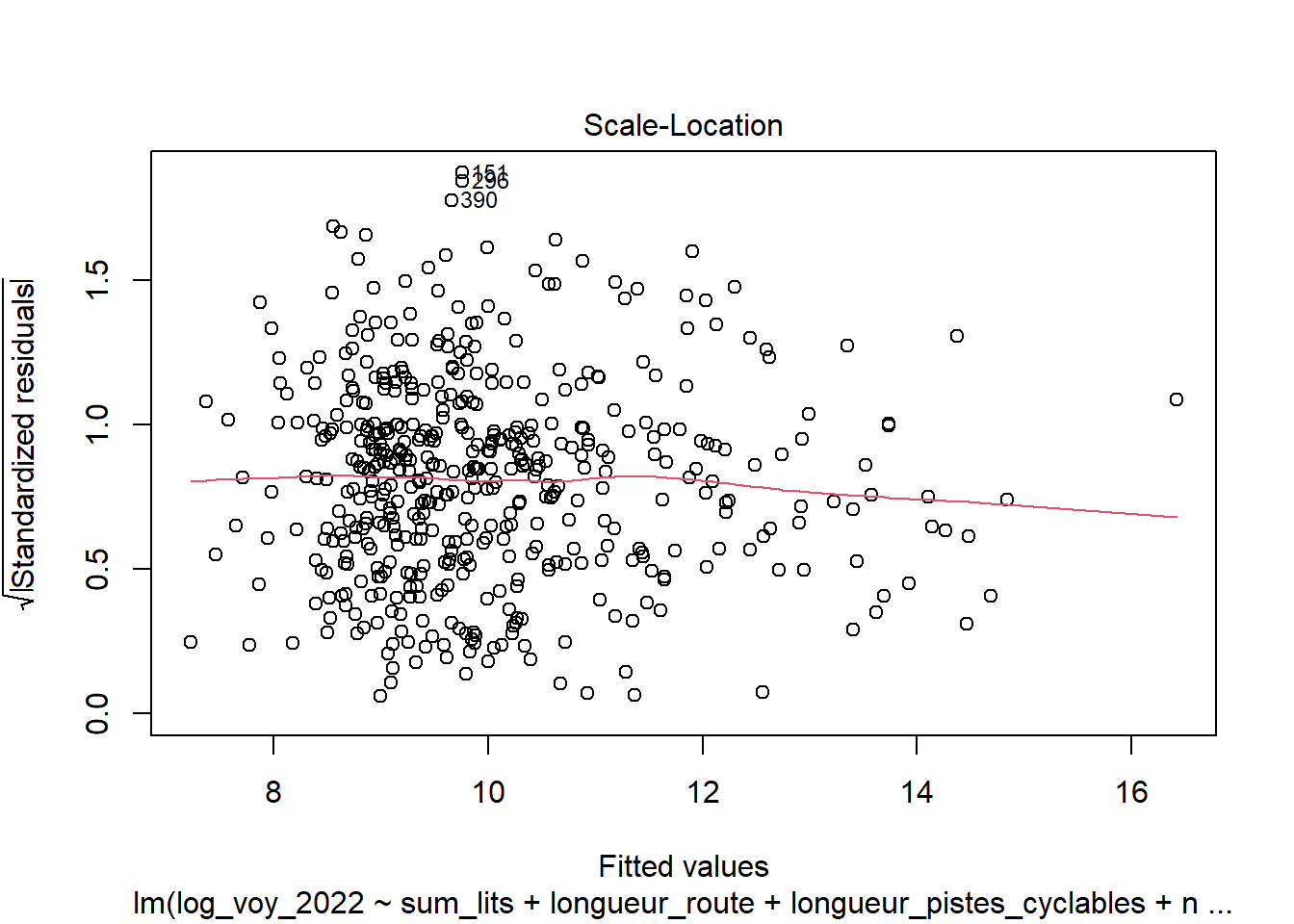
Homoscédasticité Scale-Location (ou Spread-Location) : Ce graphique montre la racine carrée des valeurs absolues des résidus standardisés en fonction des valeurs prédites. Il est utilisé pour vérifier l’homoscédasticité des résidus. Comme pour le premier graphique, une dispersion aléatoire sans motif clair est l’indicateur d’une bonne homoscédasticité. Des motifs ou des tendances peuvent indiquer des problèmes d’hétéroscédasticité. (Voir aussi test de Breusch-Pagan)
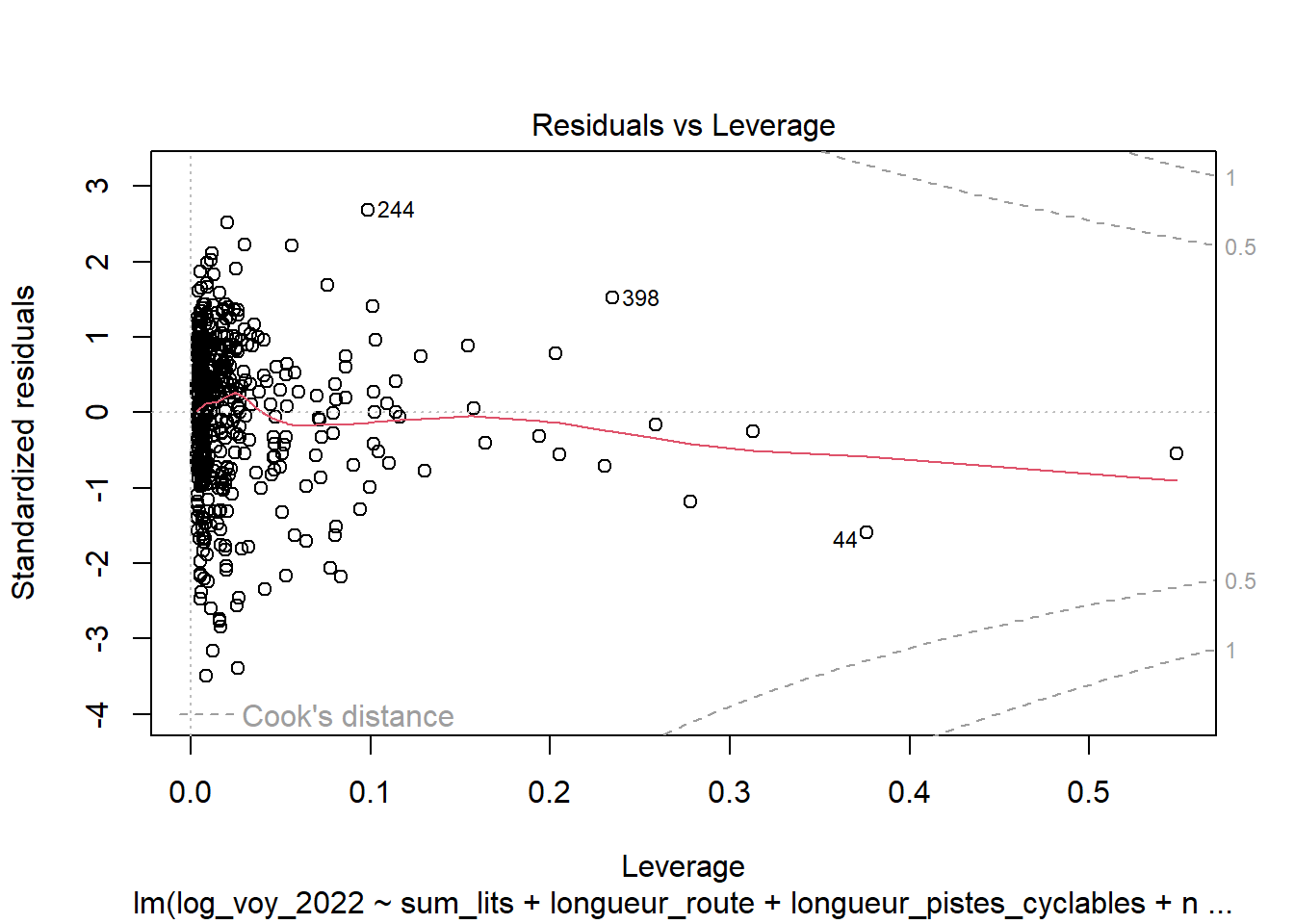
- Résidus vs Leviers (ou Leverage) : Ce graphique montre les résidus standardisés en fonction des leviers (ou valeurs de levier) pour chaque observation. Les points avec un levier élevé ont une influence plus importante sur l’ajustement du modèle. Les observations situées loin de la majorité des données (en termes de valeurs de levier) ou ayant des résidus standardisés importants sont particulièrement intéressantes car elles peuvent être des valeurs aberrantes ou des points influents.
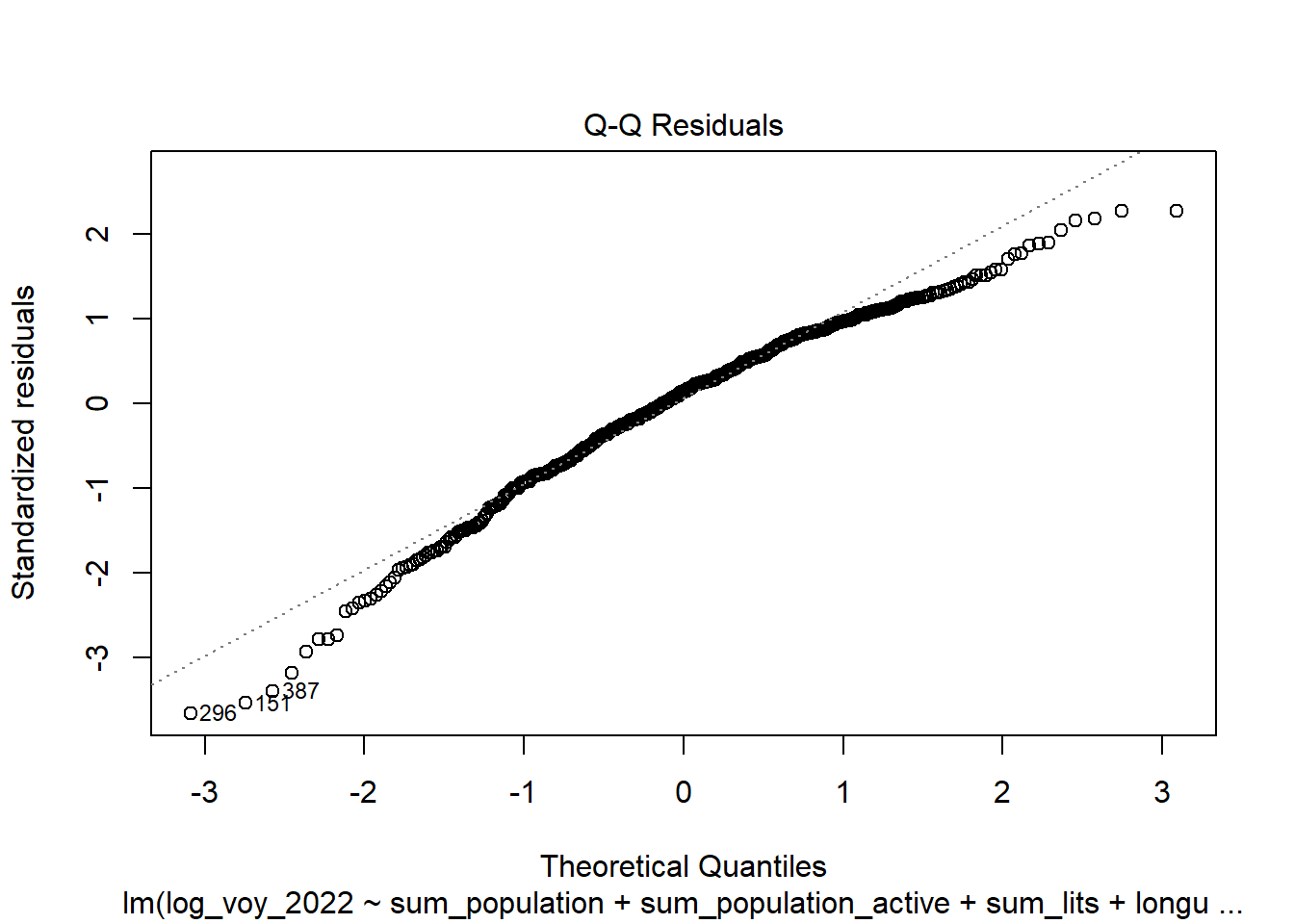
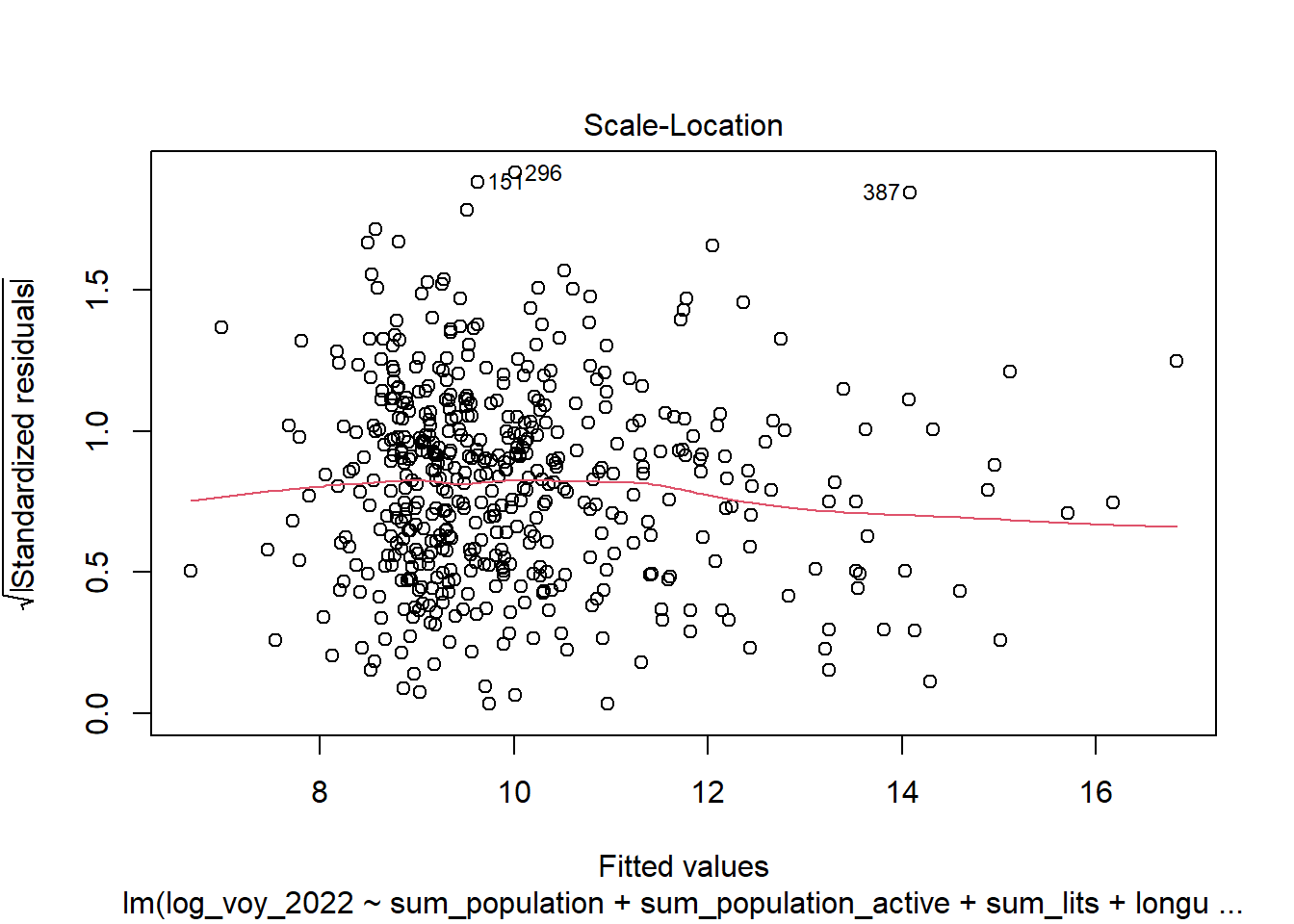
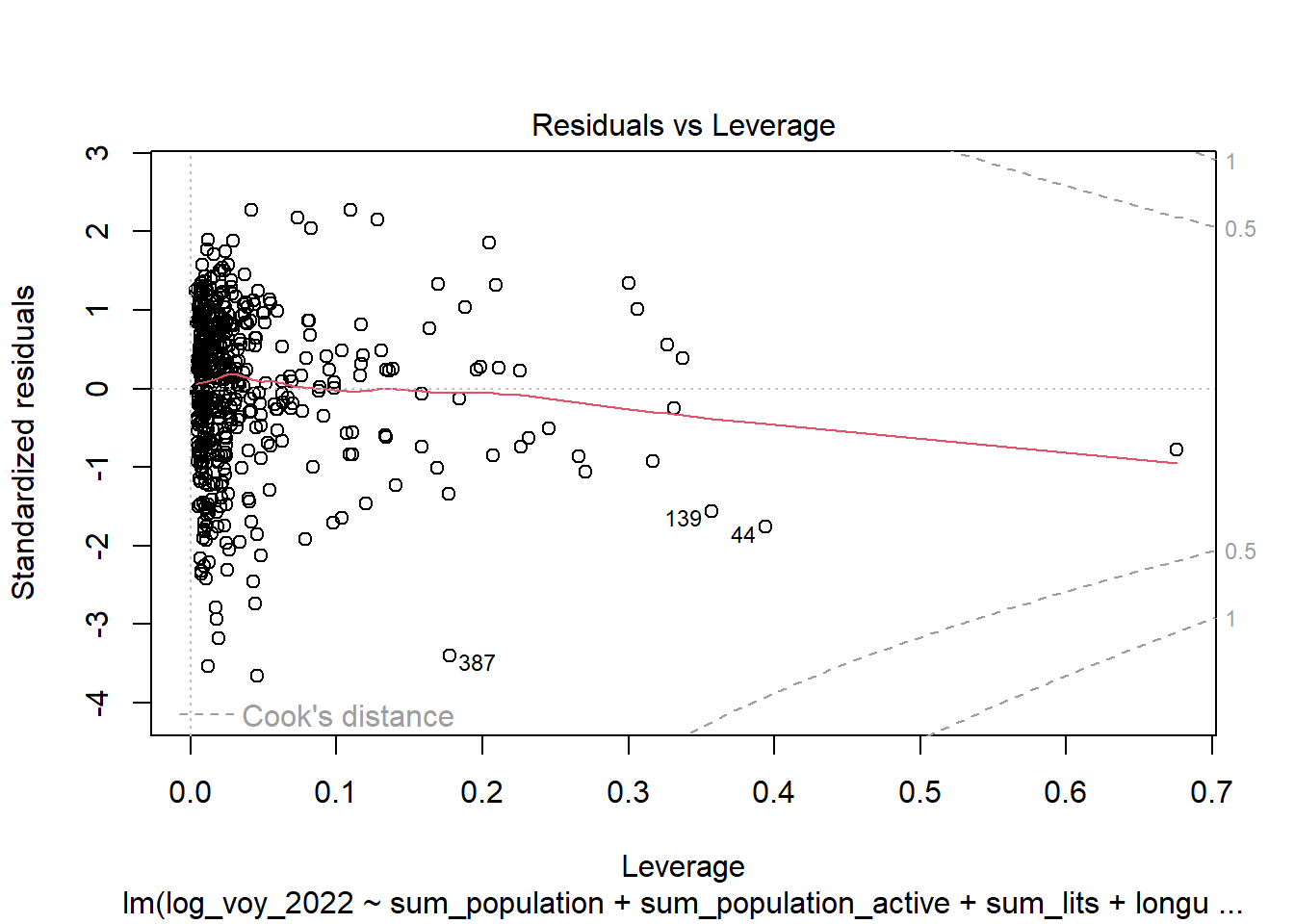
Normalité des résidus
La valeur p est de 3.855e-08, ce qui est inférieur au seuil commun de 0.05. Cela indique que nous avons suffisamment de preuves pour rejeter l’hypothèse nulle de normalité des résidus. En d’autres termes, il y a des preuves statistiques suggérant que les résidus du modèle ne suivent pas une distribution normale.
##
## Shapiro-Wilk normality test
##
## data: residuals(modele)
## W = 0.97209, p-value = 3.855e-08Homoscédasticité des résidus (homogénéité)
Avec une valeur p de 0.29899, ce test ne rejette pas l’hypothèse nulle d’homoscédasticité au seuil de significativité commun de 0.05. Cela suggère que les données ne montrent pas de preuves statistiquement significatives d’hétéroscédasticité selon ce test, et que l’assomption d’homoscédasticité (variance constante des résidus) pour le modèle de régression est raisonnablement satisfaite.
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 1.078696, Df = 1, p = 0.298995 - Multicolinéarité
L’un des points les plus importants en régression multiple est de respecter l’indépendance entre les variables exogènes (absence de colinéarité), le risque étant sinon de biaiser les estimations des erreurs types des coefficients de régression. La VIF (variance inflation factor) est une bonne méthode pour détecter ces problèmes de colinéarité.
Le “Variance Inflation Factor” (VIF) est calculé pour chaque variable explicative d’un modèle de régression. Pour calculer le VIF d’une variable, on réalise une régression de cette variable en fonction de toutes les autres variables explicatives du modèle. Le VIF est ensuite calculé comme étant 1 divisé par (1 - R²) de cette régression, où R² est le coefficient de détermination de la régression. Ainsi, le VIF mesure combien la variance d’un estimateur de régression est gonflée à cause de la multicollinéarité. La fonction vif() du package car permet de la calculer.
| Characteristic | Beta | 95% CI | p-value | VIF |
|---|---|---|---|---|
| sum_population | -34 | -59, -8.1 | 0.010 | 627 |
| sum_population_active | 34 | 6.3, 62 | 0.016 | 729 |
| sum_lits | -3.1 | -7.6, 1.5 | 0.2 | 18 |
| longueur_route | 7.7 | 1.6, 14 | 0.014 | 41 |
| nb_intersections | 2.8 | -2.2, 7.9 | 0.3 | 30 |
| longueur_pistes_cyclables | -1.5 | -3.1, 0.10 | 0.066 | 1.8 |
| nombre_arrets | 3.4 | 1.0, 5.8 | 0.005 | 2.3 |
| nombre_parkings | 2.9 | 0.54, 5.3 | 0.016 | 1.7 |
| nombre_commerces | -11 | -17, -4.0 | 0.002 | 7.8 |
| nombre_sante | 1.8 | -0.58, 4.1 | 0.14 | 3.9 |
| nombre_loisirs | -2.6 | -5.1, -0.14 | 0.039 | 3.8 |
| nombre_restauration | 12 | 5.3, 20 | <0.001 | 9.5 |
| nombre_sports | 0.61 | -2.4, 3.6 | 0.7 | 2.1 |
| nombre_ronds_points | 0.18 | -1.1, 1.4 | 0.8 | 2.0 |
| nombre_eleves | 0.14 | -1.2, 1.5 | 0.8 | 1.5 |
| ZA | -2.6 | -4.9, -0.35 | 0.024 | 5.9 |
| passage_niveau | -1.6 | -2.6, -0.65 | 0.001 | 1.2 |
| sum_population_carreau | -1.6 | -3.8, 0.54 | 0.14 | 6.3 |
| PNR_OK | -0.23 | -0.74, 0.28 | 0.4 | 1.1 |
| Abbreviations: CI = Confidence Interval, VIF = Variance Inflation Factor | ||||
Les valeurs du Facteur d’Inflation de la Variance (VIF) fournissent une indication de la présence de multicolinéarité parmi les variables explicatives dans un modèle de régression linéaire. En règle générale, un VIF supérieur à 5 est souvent considéré comme indiquant une forte multicolinéarité, nécessitant une action pour réduire cette multicollinéarité dans le modèle.
6 - Construction du modèle de régression linéaire avec moins de variable (VIF < 5)
Nous avons procédé de manière itérative en supprimant des variables au fur et à mesure. Finalement nous conservons les valeurs suivantes :
- sum_lits
- longueur_route
- longueur_pistes_cyclables
- nombre_arrets
- nombre_parkings
- nombre_commerces
- nombre_sports
- nombre_ronds_points
- nombre_eleves
- passage_niveau
- sum_population_carreau
- PNR_OK
- pente (pour le vélo)
modele <- lm(
log_voy_2022 ~
# sum_population+
# sum_population_active+
sum_lits+
longueur_route+
# nb_intersections+
# reseau_pedestre+
longueur_pistes_cyclables+
nombre_arrets+
nombre_parkings+
nombre_commerces+
# nombre_sante+
# nombre_loisirs+
# nombre_restauration+
nombre_sports+
nombre_ronds_points+
nombre_eleves+
# ZA+
passage_niveau+
sum_population_carreau+
PNR_OK,
data = all_data_filter
)Affichage du résumé du modèle pour voir les coefficients et la significativité des variables
##
## Call:
## lm(formula = log_voy_2022 ~ sum_lits + longueur_route + longueur_pistes_cyclables +
## nombre_arrets + nombre_parkings + nombre_commerces + nombre_sports +
## nombre_ronds_points + nombre_eleves + passage_niveau + sum_population_carreau +
## PNR_OK, data = all_data_filter)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.8108 -1.2167 0.1972 1.4069 4.9833
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.5266 0.2009 42.440 < 2e-16 ***
## sum_lits -1.9555 0.6921 -2.826 0.00491 **
## longueur_route 6.9574 1.1020 6.313 6.17e-10 ***
## longueur_pistes_cyclables -0.6509 0.8035 -0.810 0.41830
## nombre_arrets 2.4199 1.1462 2.111 0.03527 *
## nombre_parkings 2.9557 1.2282 2.406 0.01648 *
## nombre_commerces -1.6165 1.8779 -0.861 0.38979
## nombre_sports 0.9617 1.5137 0.635 0.52551
## nombre_ronds_points 0.3131 0.6267 0.500 0.61764
## nombre_eleves 0.6110 0.6973 0.876 0.38135
## passage_niveau -2.0668 0.4977 -4.153 3.88e-05 ***
## sum_population_carreau -0.7852 0.9468 -0.829 0.40734
## PNR_OK -0.1757 0.2609 -0.674 0.50086
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.955 on 485 degrees of freedom
## Multiple R-squared: 0.3415, Adjusted R-squared: 0.3252
## F-statistic: 20.96 on 12 and 485 DF, p-value: < 2.2e-16Un modèle de régression linéaire multiple permet de faire trois choses principales avec les variables d’une étude :
Trouver des Coefficients : le modèle donne un coefficient (un nombre) pour chaque variable indépendante examinée. Ce coefficient nous dit comment, et de combien, on peut s’attendre à ce que la variable dépendante change quand la variable indépendante change d’une unité, en gardant toutes les autres variables constantes.
Juger de leur Force : La taille ou la valeur absolue de chaque coefficient nous donne une idée de la force de l’effet de cette variable indépendante sur la variable dépendante. Un grand coefficient (en valeur absolue) signifie un grand effet : si la variable indépendante augmente d’un peu, la variable dépendante change de beaucoup.
Évaluer leur Significativité : Le modèle nous donne aussi une valeur p pour chaque coefficient, qui nous dit si l’effet observé est statistiquement significatif. Une valeur p faible (souvent moins de 0,05) suggère que l’effet n’est probablement pas dû au hasard, et que la variable indépendante a vraiment un impact sur la variable dépendante.
En somme, la régression linéaire multiple est un outil utile pour comprendre et quantifier les relations entre une variable dépendante et plusieurs variables indépendantes, en nous permettant de voir non seulement quels facteurs sont importants, mais aussi comment ils sont importants.
- valeur t comme à un score de force ou de clarté de
l’observation
- valeur p comme à un indicateur de l’importance ou de la
significativité del’observation
- Normalement, une valeur t élevée indique une différence marquée entre le groupe observé et le groupe de référence, ce qui conduit généralement à une valeur p faible, suggérant que les résultats sont statistiquement significatifs.
Coefficient de détermination
## [1] 0.3414632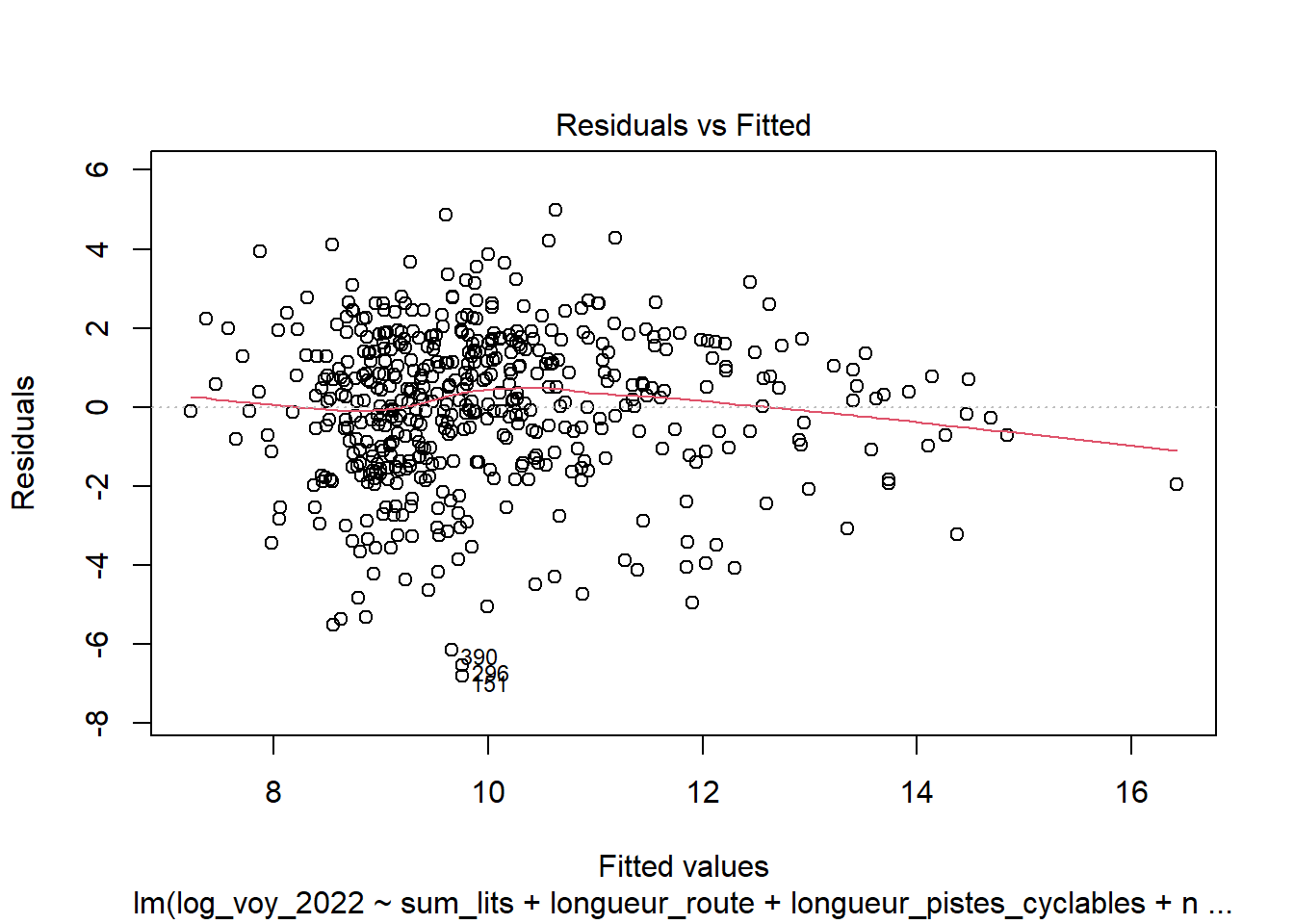
##
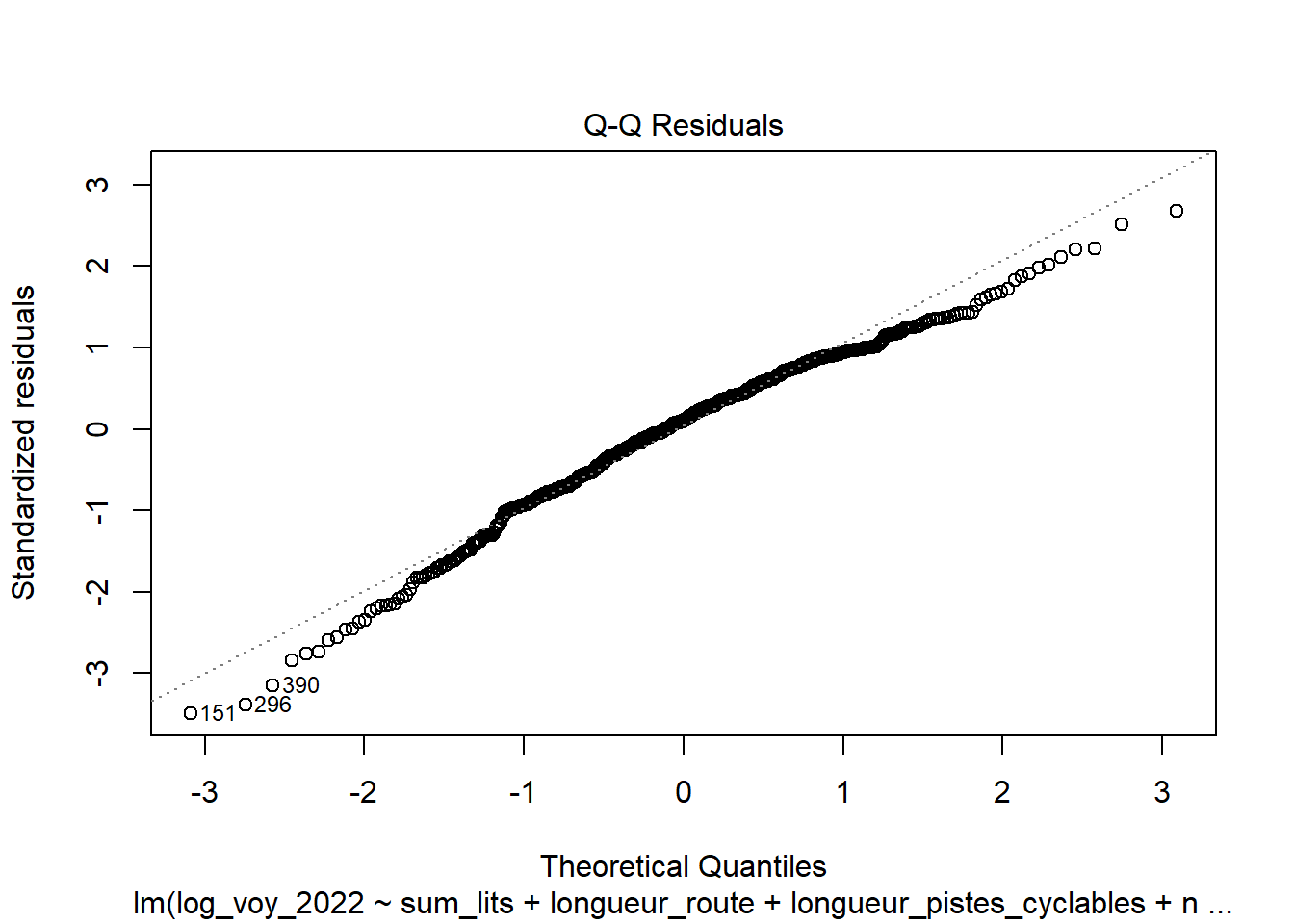
## Shapiro-Wilk normality test
##
## data: residuals(modele)
## W = 0.97883, p-value = 1.24e-06## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
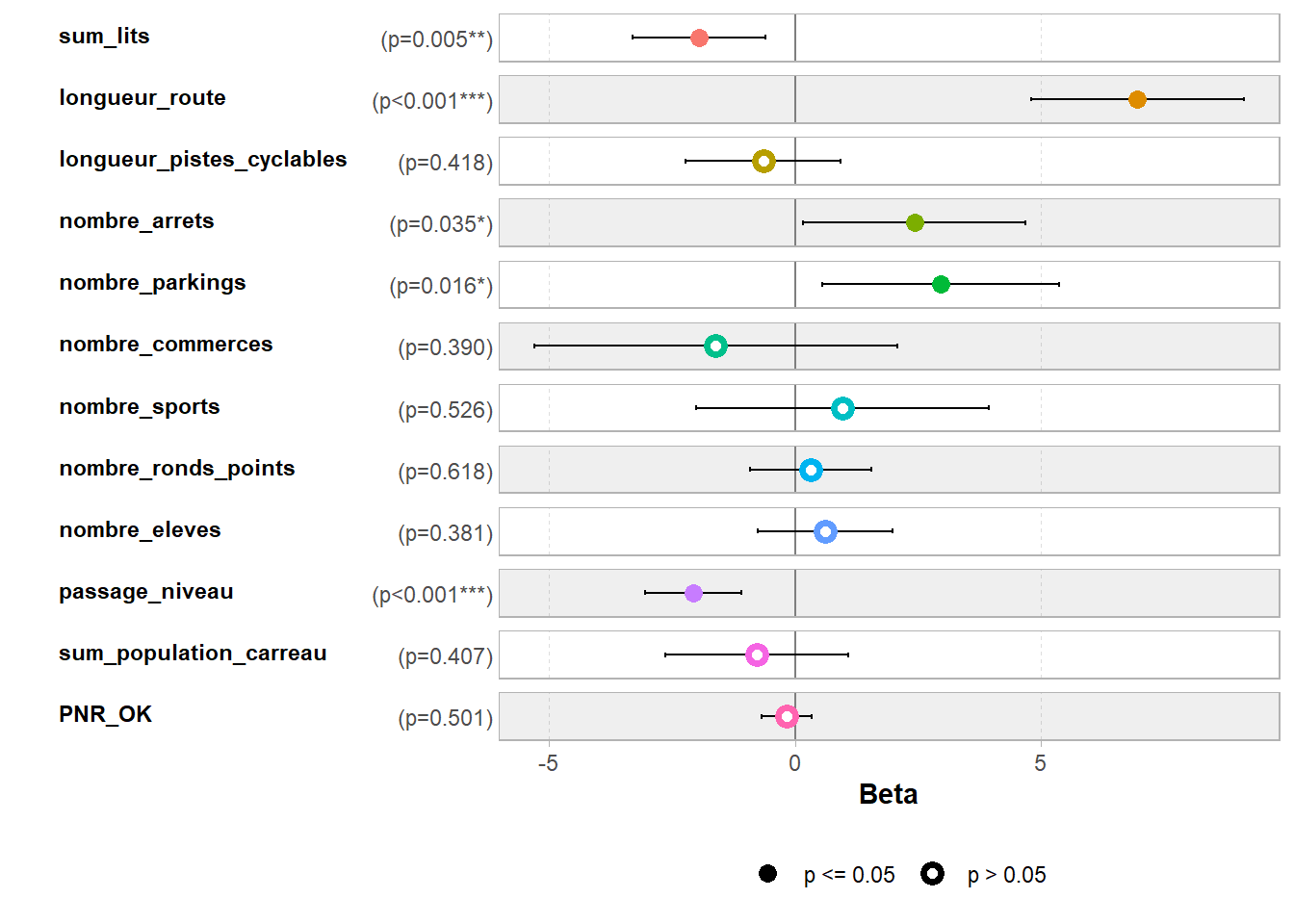
## Chisquare = 0.9095079, Df = 1, p = 0.34025# Avec le package gtsummary :
gtsummary::tbl_regression(modele) %>%
gtsummary::add_vif()%>%
gtsummary::as_gt() %>%
gt::tab_footnote(
footnote = "Données Hauts-de-France")| Characteristic | Beta | 95% CI | p-value | VIF |
|---|---|---|---|---|
| sum_lits | -2.0 | -3.3, -0.60 | 0.005 | 1.5 |
| longueur_route | 7.0 | 4.8, 9.1 | <0.001 | 4.9 |
| longueur_pistes_cyclables | -0.65 | -2.2, 0.93 | 0.4 | 1.7 |
| nombre_arrets | 2.4 | 0.17, 4.7 | 0.035 | 1.9 |
| nombre_parkings | 3.0 | 0.54, 5.4 | 0.016 | 1.6 |
| nombre_commerces | -1.6 | -5.3, 2.1 | 0.4 | 2.3 |
| nombre_sports | 0.96 | -2.0, 3.9 | 0.5 | 2.0 |
| nombre_ronds_points | 0.31 | -0.92, 1.5 | 0.6 | 1.8 |
| nombre_eleves | 0.61 | -0.76, 2.0 | 0.4 | 1.4 |
| passage_niveau | -2.1 | -3.0, -1.1 | <0.001 | 1.1 |
| sum_population_carreau | -0.79 | -2.6, 1.1 | 0.4 | 4.4 |
| PNR_OK | -0.18 | -0.69, 0.34 | 0.5 | 1.0 |
| Abbreviations: CI = Confidence Interval, VIF = Variance Inflation Factor | ||||
| Données Hauts-de-France | ||||
library(ggplot2)
ggplot(data = all_data_filter, aes(x = longueur_route, y = log_voy_2022)) +
geom_point() +
theme_minimal() +
labs(x = "longueur_route", y = "Nombre de voyageurs", title = "Relation entre la longueur_route et le nombre de voyageurs")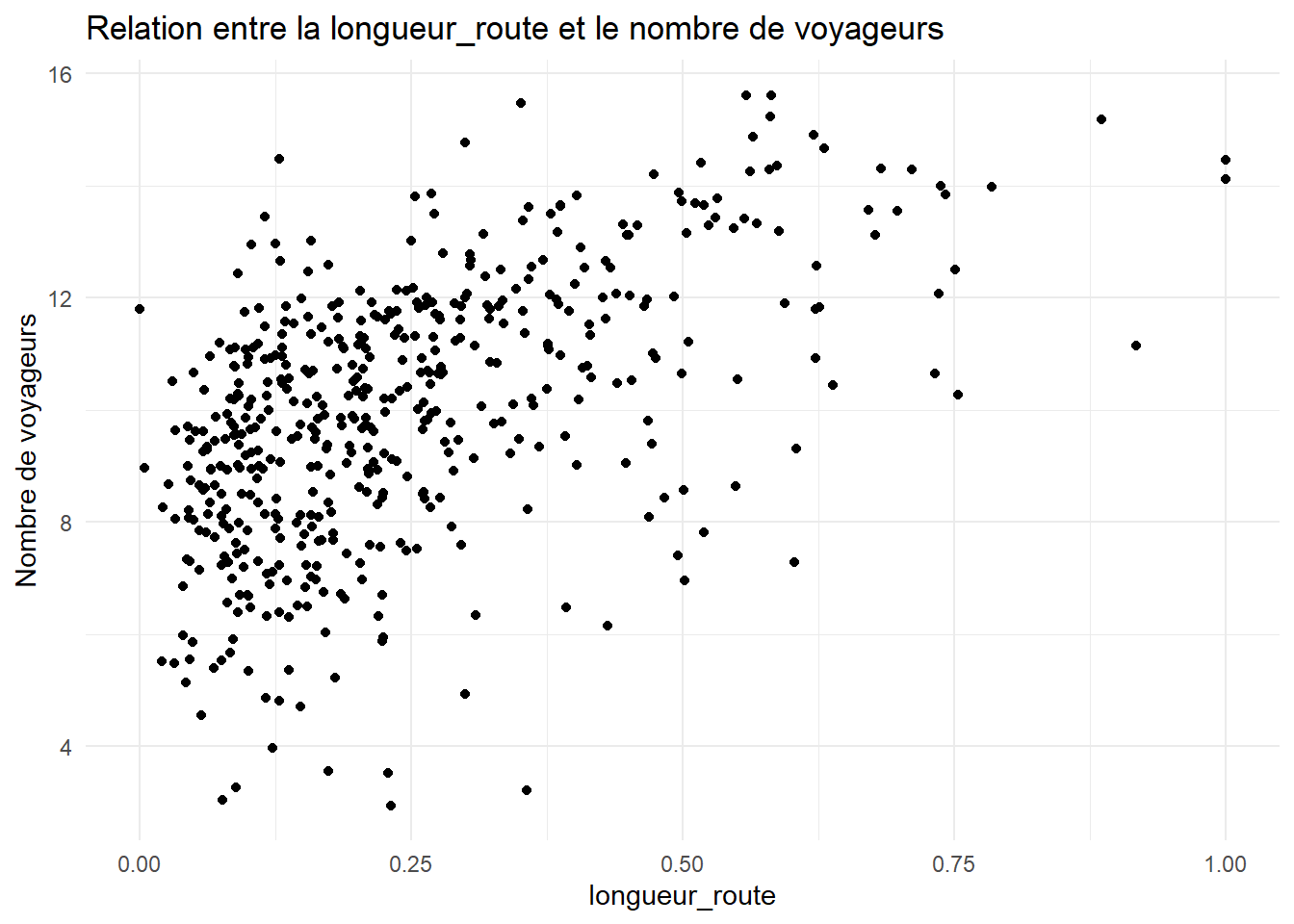
ggplot(data = all_data_filter, aes(x = nombre_arrets, y = log_voy_2022)) +
geom_point() +
theme_minimal() +
labs(x = "nombre_arrets", y = "Nombre de voyageurs", title = "Relation entre nombre_arrets et le nombre de voyageurs")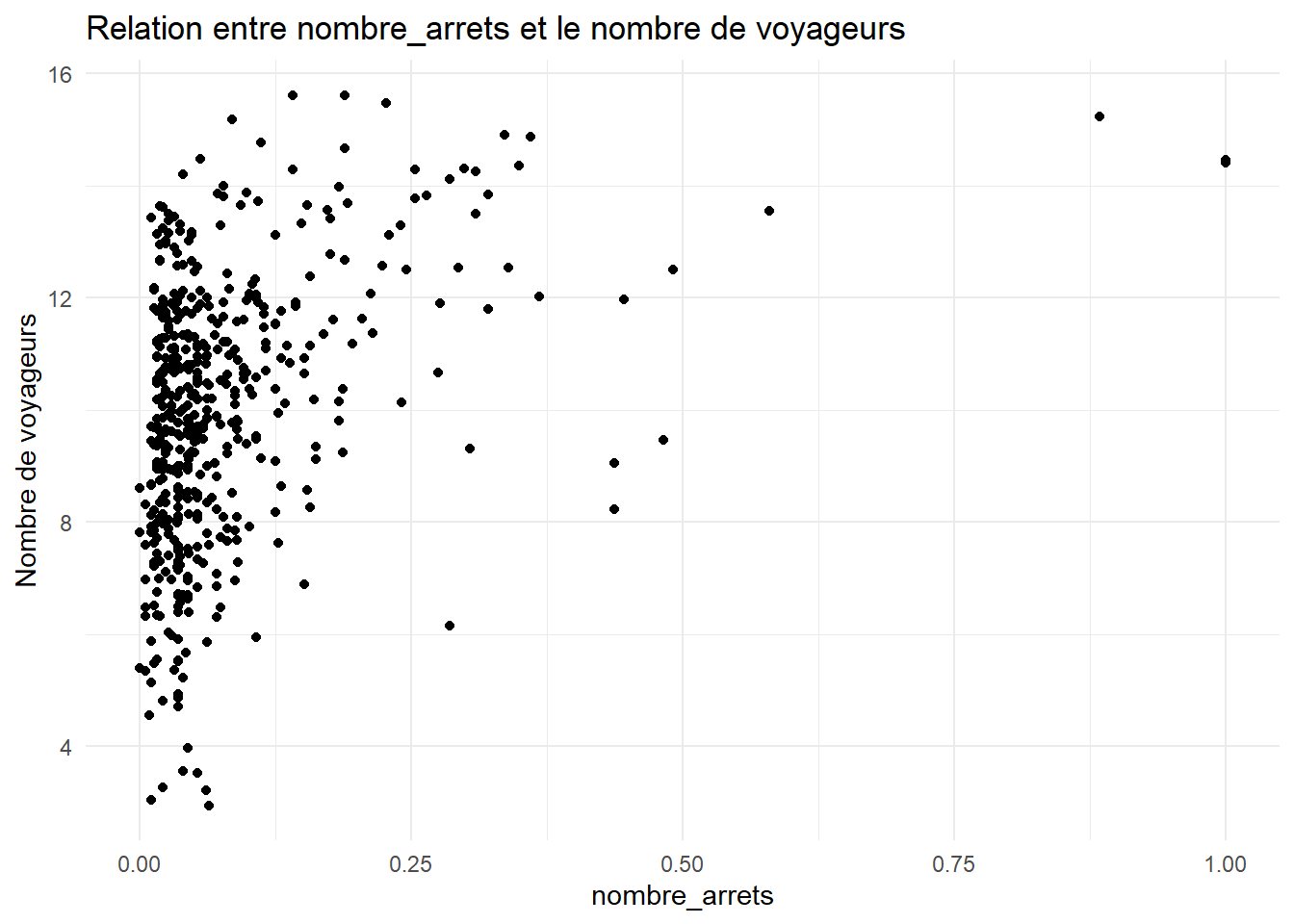
ggplot(data = all_data_filter, aes(x = nombre_parkings, y = log_voy_2022)) +
geom_point() +
theme_minimal() +
labs(x = "nombre_parkings", y = "Nombre de voyageurs", title = "Relation entre nombre_parkings et le nombre de voyageurs")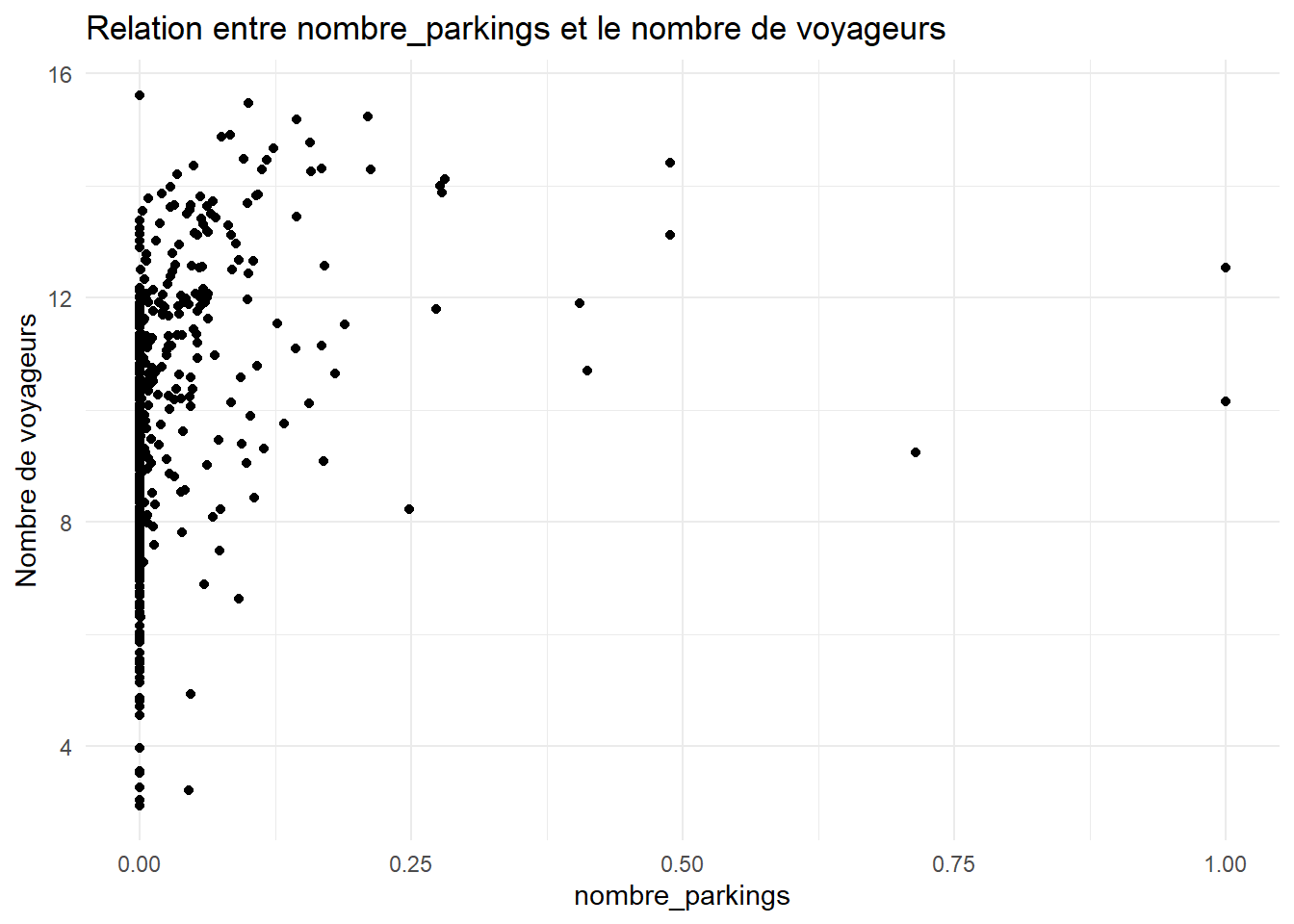
ggplot(data = all_data_filter, aes(x = sum_lits, y = log_voy_2022)) +
geom_point() +
theme_minimal() +
labs(x = "sum_lits", y = "Nombre de voyageurs", title = "Relation entre la sum_lits et le nombre de voyageurs")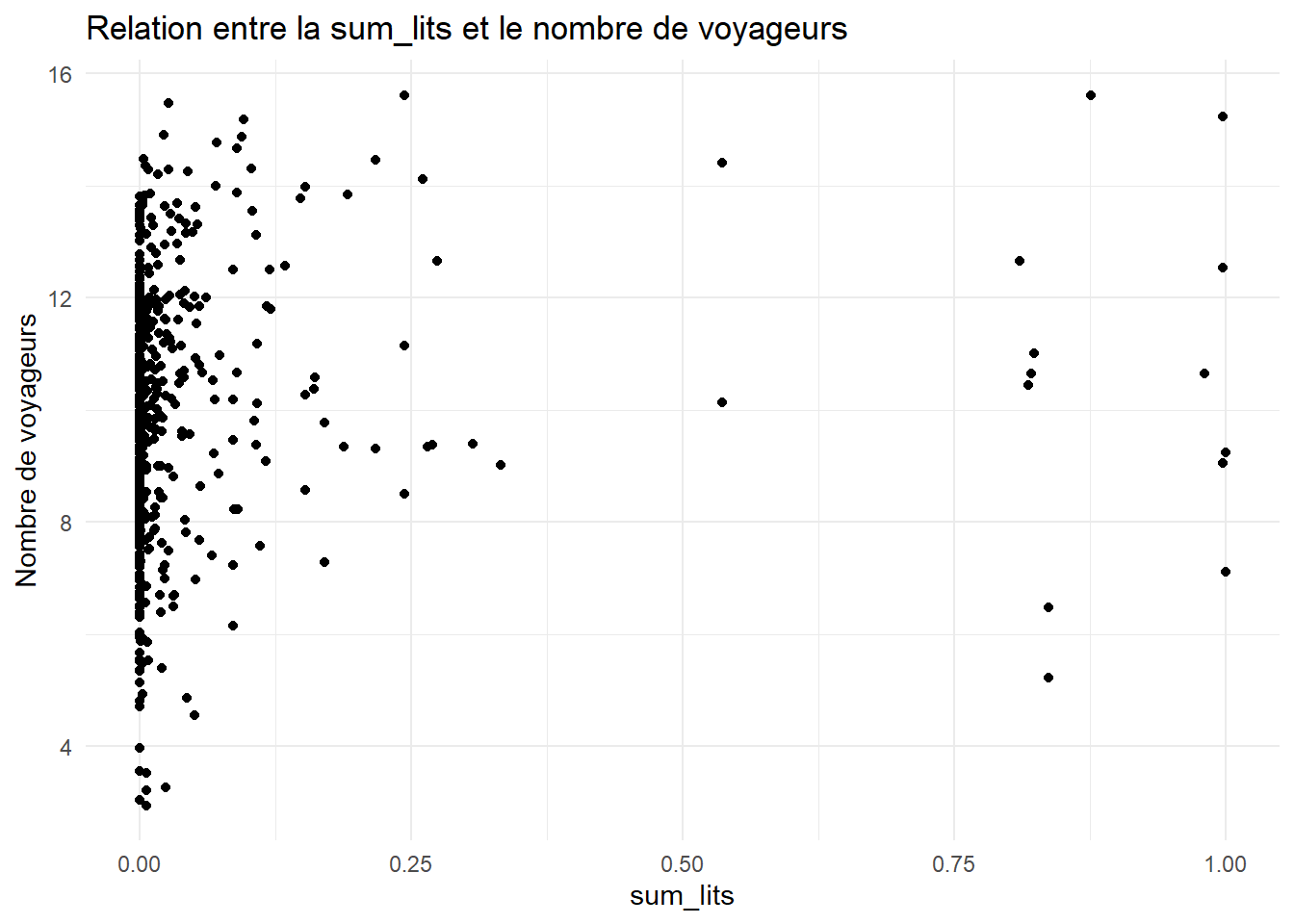
ggplot(data = all_data_filter, aes(x = passage_niveau, y = log_voy_2022)) +
geom_point() +
theme_minimal() +
labs(x = "passage_niveau", y = "Nombre de voyageurs", title = "Relation entre passage_niveau et le nombre de voyageurs")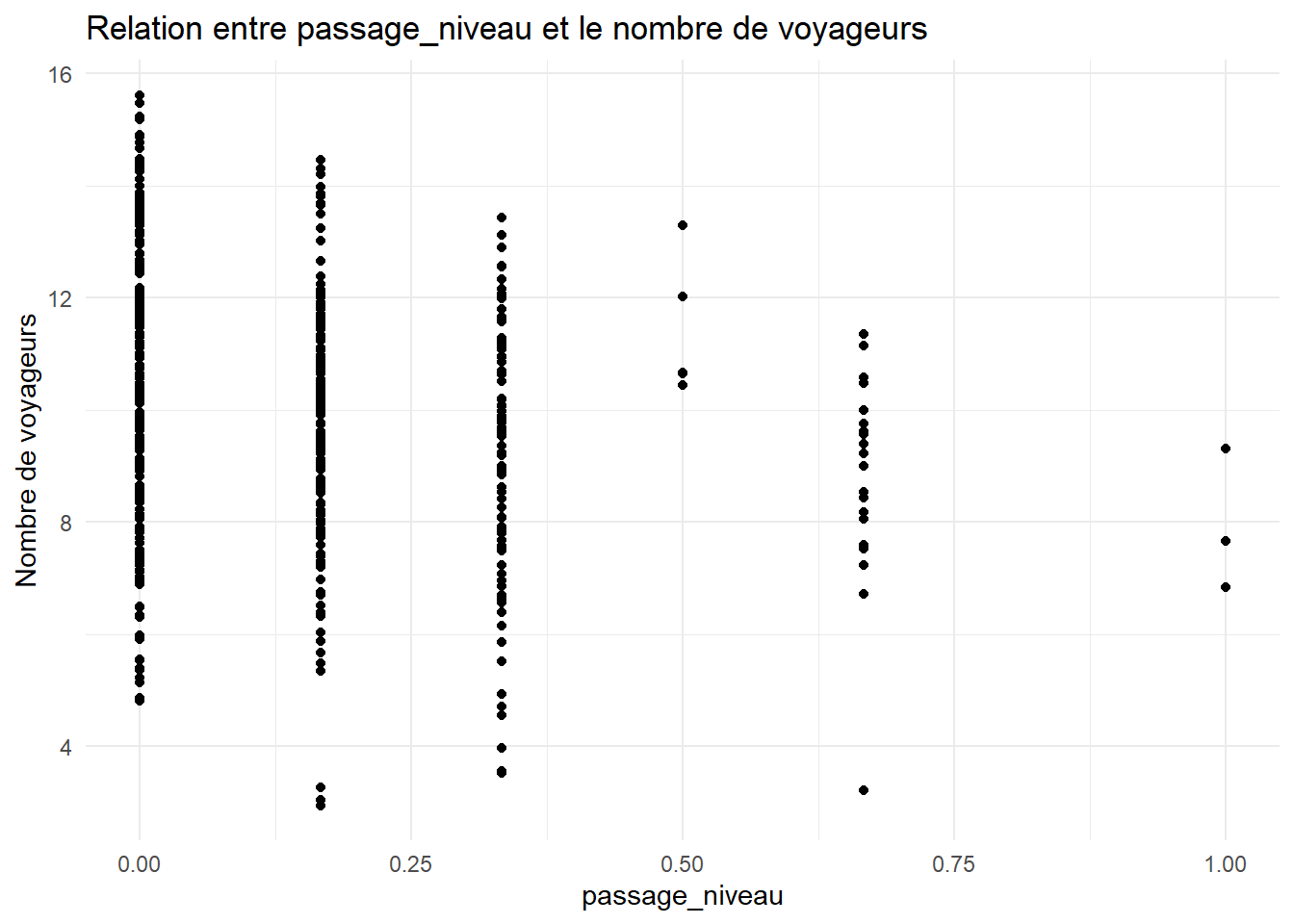
7 - Analyse en composantes principales (ACP)
## Rows: 498
## Columns: 24
## $ ID_number <chr> "Pont de la Deûle", "Les Bons-Pères", "Maube…
## $ voy_2022 <dbl> 24168, 554, 513226, 1989, 238, 3920113, 1494…
## $ sum_population <dbl> 0.1751477517, 0.0189921255, 0.1192634891, 0.…
## $ sum_population_active <dbl> 0.1507132358, 0.0174699951, 0.0942287243, 0.…
## $ sum_lits <dbl> 0.0329117367, 0.0000000000, 0.0425676595, 0.…
## $ longueur_route <dbl> 0.34396799, 0.21975495, 0.50399247, 0.296212…
## $ nb_intersections <dbl> 0.27310924, 0.22899160, 0.51995798, 0.279411…
## $ longueur_pistes_cyclables <dbl> 0.036460243, 0.057294562, 0.080591151, 0.000…
## $ nombre_arrets <dbl> 0.088000000, 0.005333333, 0.026666667, 0.064…
## $ nombre_parkings <dbl> 0.0001071123, 0.0000000000, 0.0502356470, 0.…
## $ nombre_commerces <dbl> 0.004201681, 0.000000000, 0.031512605, 0.008…
## $ nombre_sante <dbl> 0.106796117, 0.000000000, 0.019417476, 0.019…
## $ nombre_loisirs <dbl> 0.01176471, 0.00000000, 0.02352941, 0.047058…
## $ nombre_restauration <dbl> 0.007984032, 0.001996008, 0.059880240, 0.005…
## $ nombre_sports <dbl> 0.00000000, 0.00000000, 0.09090909, 0.000000…
## $ nombre_ronds_points <dbl> 0.2, 0.2, 0.6, 0.3, 0.0, 0.2, 0.0, 0.0, 0.2,…
## $ nombre_eleves <dbl> 0.0000000, 0.0000000, 0.0000000, 0.1255887, …
## $ ZA <dbl> 0.3966329, 0.3235975, 0.4251031, 0.5001756, …
## $ passage_niveau <dbl> 0.1666667, 0.0000000, 0.0000000, 0.6666667, …
## $ sum_population_carreau <dbl> 0.2364492977, 0.0875346748, 0.1503236317, 0.…
## $ PNR_OK <dbl> 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ geom <POINT [m]> POINT (706054.2 7033395), POINT (77214…
## $ log_voy_2022 <dbl> 10.092785, 6.317165, 13.148472, 7.595387, 5.…
## $ cluster <fct> 1, 1, 2, 1, 1, 3, 1, 1, 1, 3, 1, 1, 1, 1, 1,…data_select <- all_data_filter %>%
select(# sum_population+
# sum_population_active+
sum_lits,
longueur_route,
# nb_intersections+
# reseau_pedestre+
longueur_pistes_cyclables,
nombre_arrets,
nombre_parkings,
nombre_commerces,
# nombre_sante+
# nombre_loisirs+
# nombre_restauration+
nombre_sports,
nombre_ronds_points,
nombre_eleves,
# ZA+
passage_niveau,
sum_population_carreau,
PNR_OK
) %>%
sf::st_drop_geometry()# Coefficient de corrélation de PEARSON
# Ces coefficients mesurent la force et la direction de la relation linéaire entre chaque paire de variables
stats::cor(data_select, use = "complete.obs")# Lancement de l'ACP
PCA <- FactoMineR::PCA(data_select,
quanti.sup = c(),
quali.sup = c("PNR_OK"), # valeur binaire traitée comme une variable supplémentaire
scale.unit = T) # normalisation des variables## Warning in geom_bar(stat = "identity", fill = barfill, color = barcolor, :
## Ignoring empty aesthetic: `width`.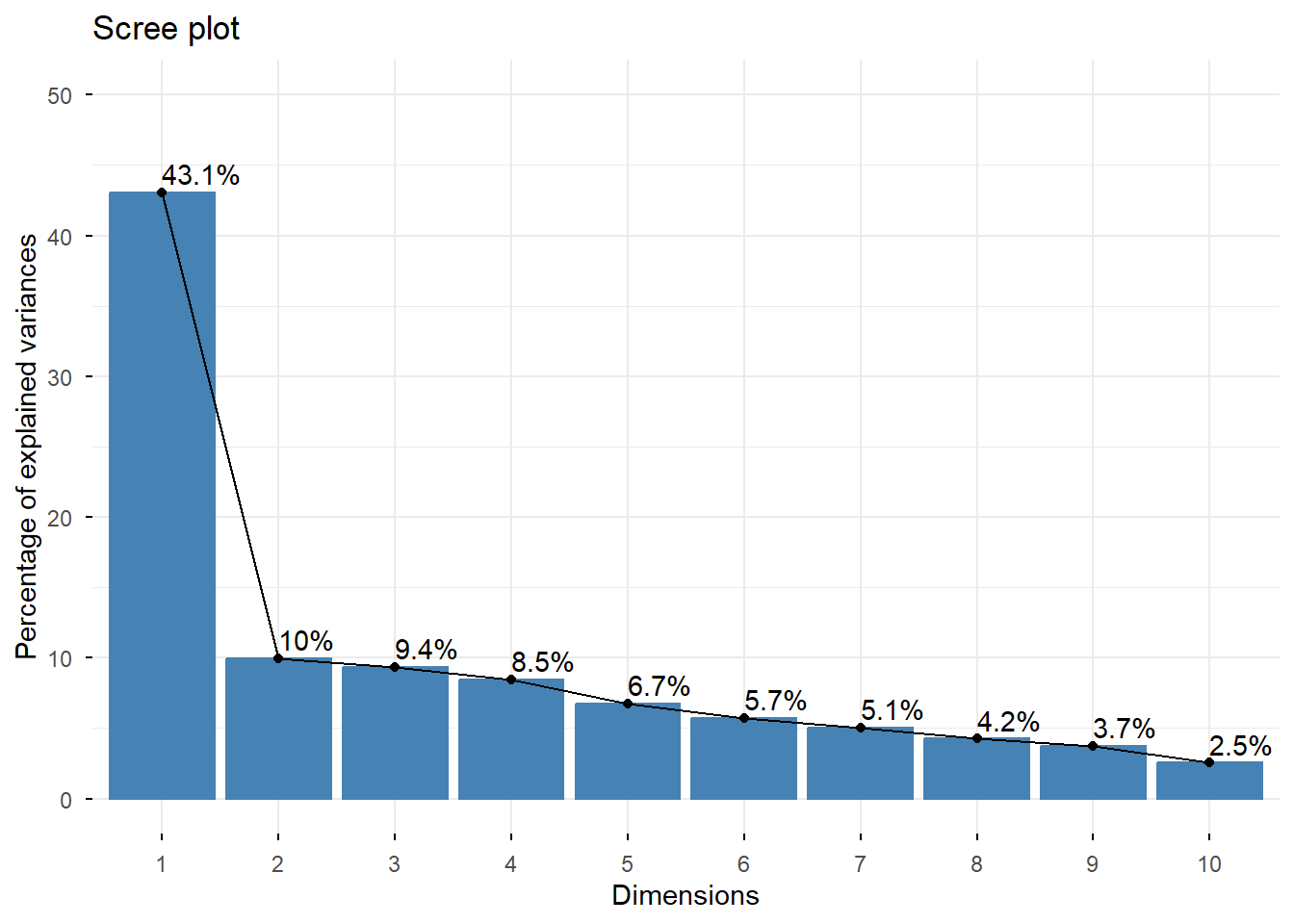
# Cercle des corrélations
factoextra::fviz_pca_var(PCA, col.var="contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)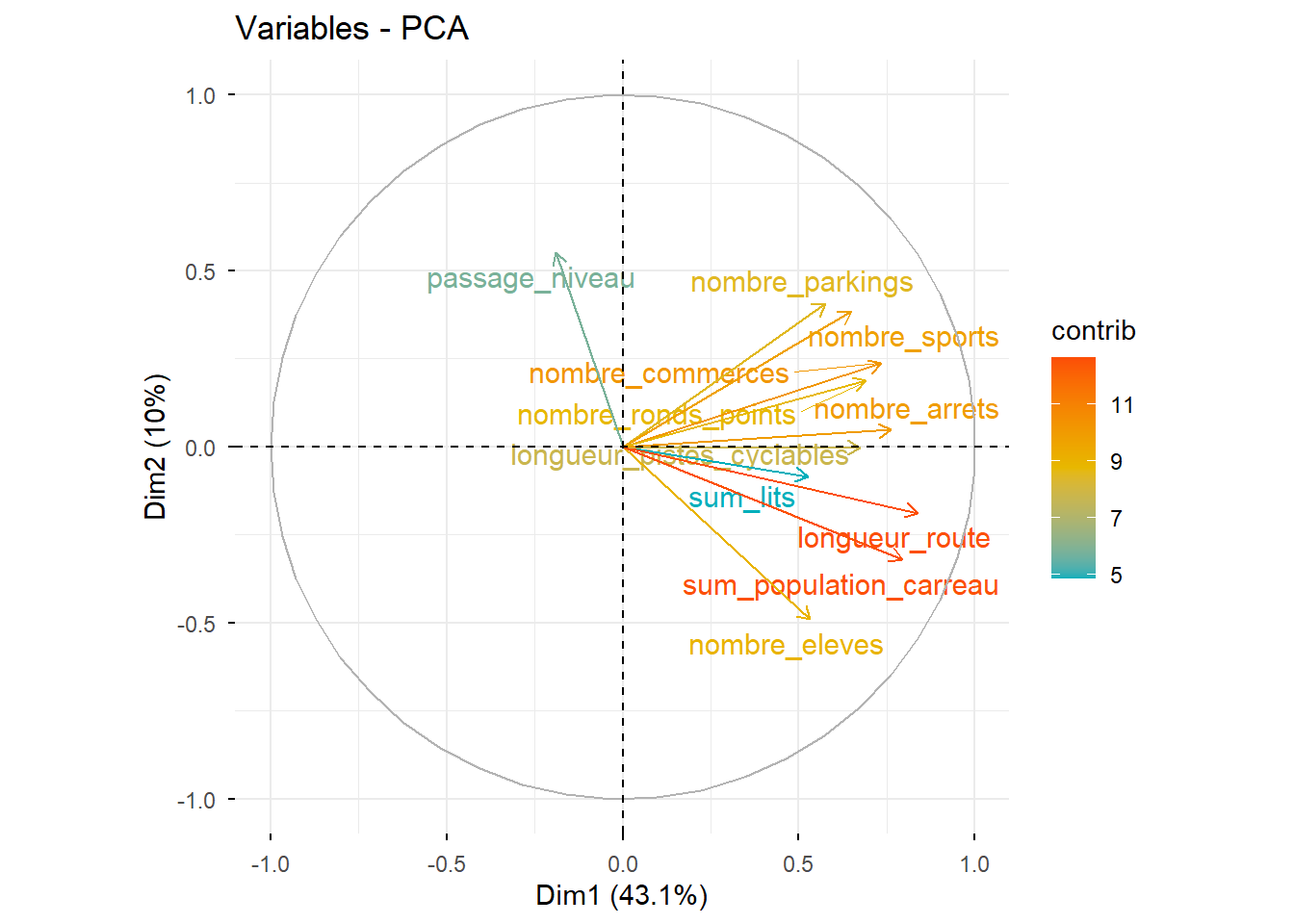
# Graphique des individus
factoextra::fviz_pca_ind(PCA, col.ind = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)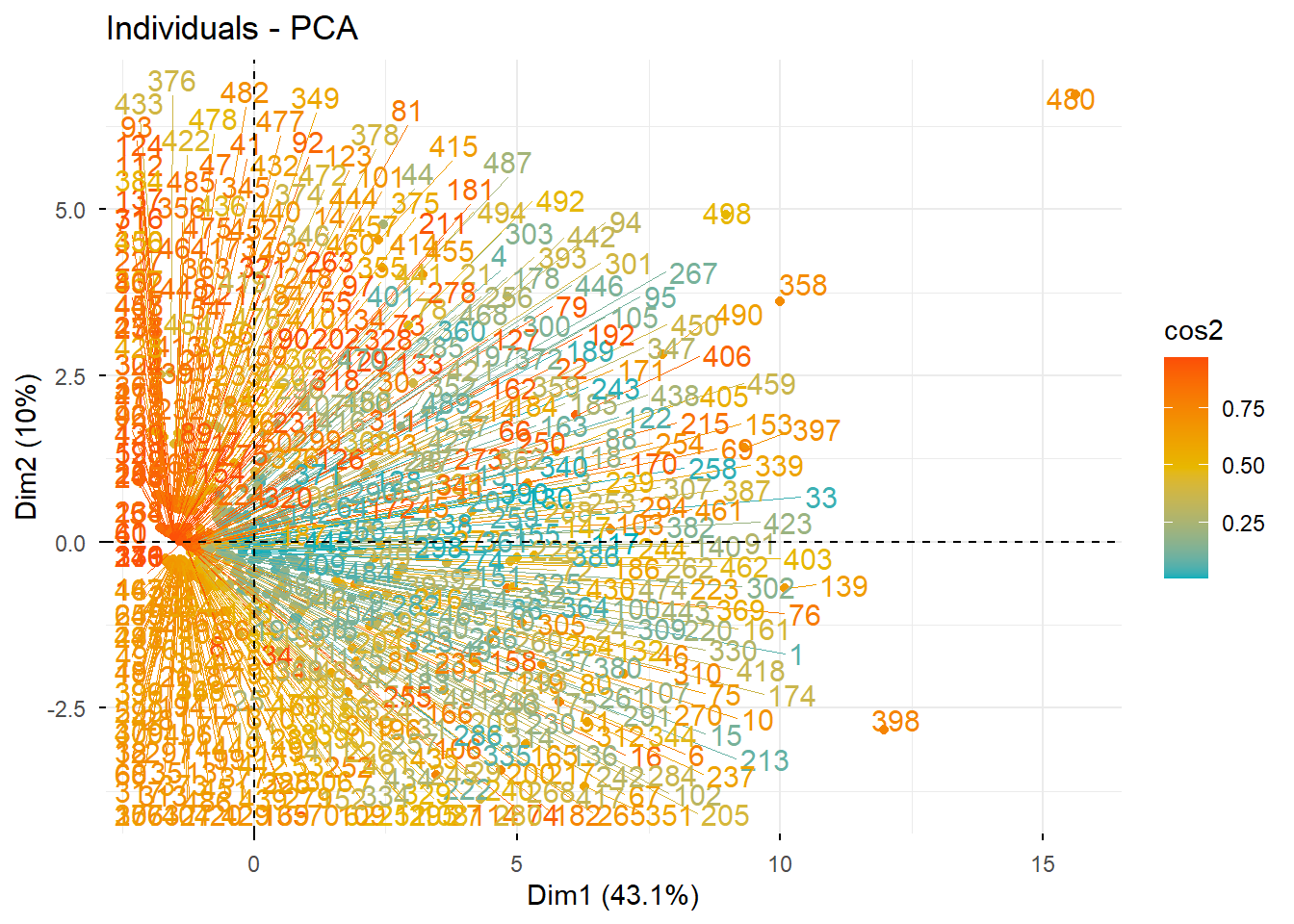
## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 4.7371548 43.065044 43.06504
## comp 2 1.0959291 9.962992 53.02804
## comp 3 1.0287654 9.352413 62.38045
## comp 4 0.9299004 8.453640 70.83409
## comp 5 0.7421077 6.746434 77.58052
## comp 6 0.6314726 5.740660 83.32118
## comp 7 0.5557962 5.052692 88.37387
## comp 8 0.4673489 4.248626 92.62250
## comp 9 0.4118871 3.744429 96.36693
## comp 10 0.2801946 2.547223 98.91415
## comp 11 0.1194432 1.085847 100.00000# Contribution de chaque variable aux deux premiers axes
factoextra::fviz_contrib(PCA, choice = "var", axes = 1) # axe 1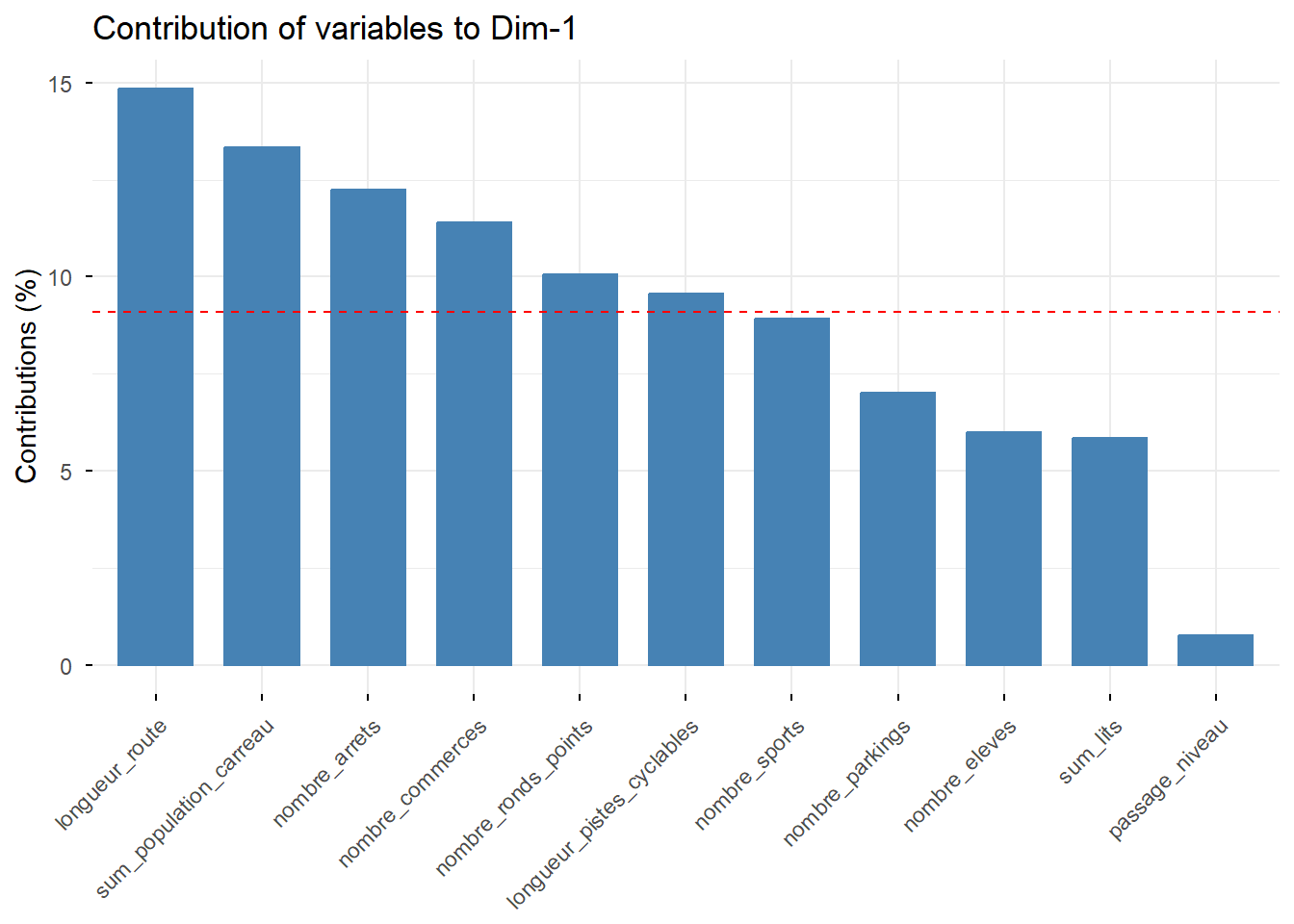
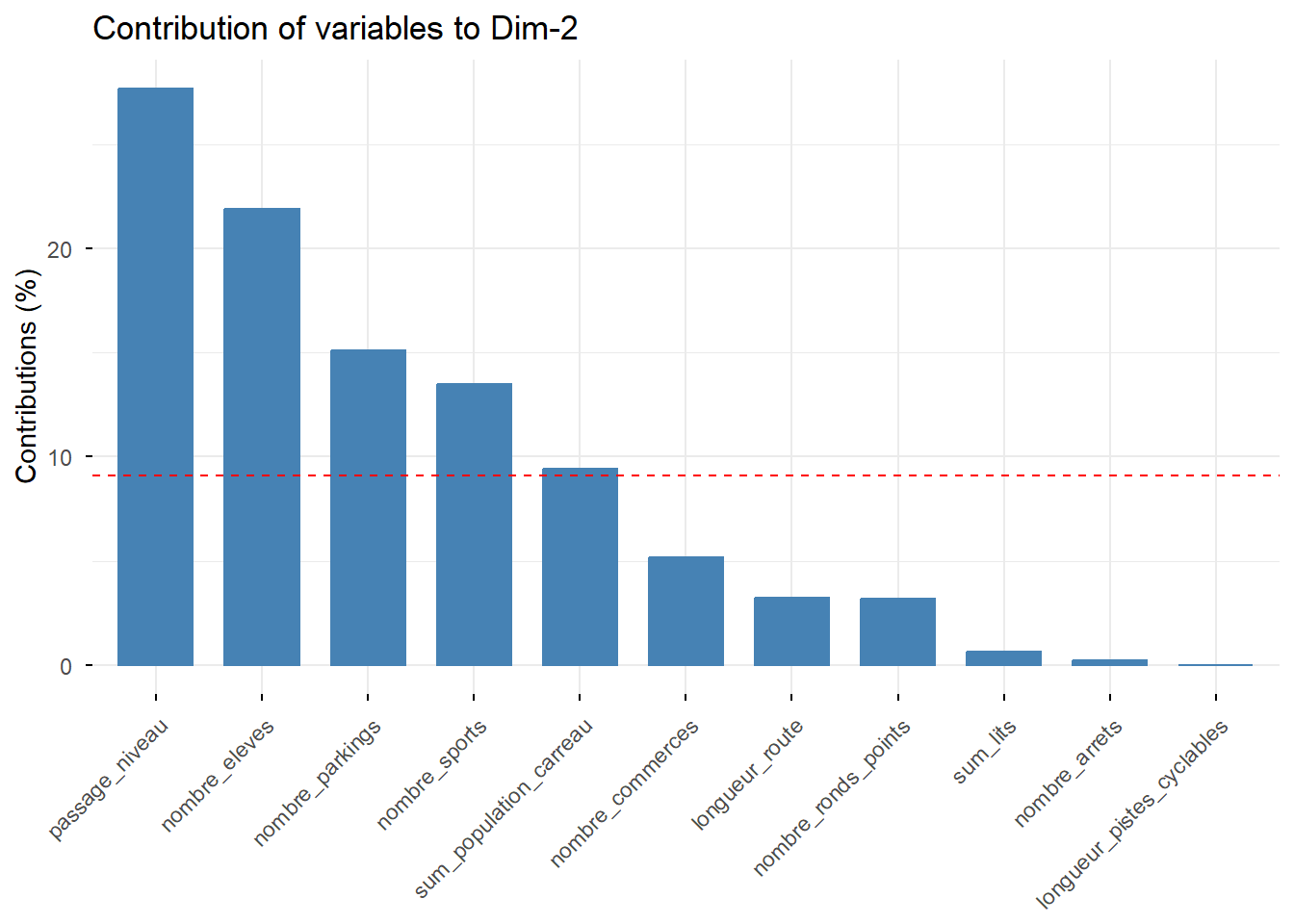
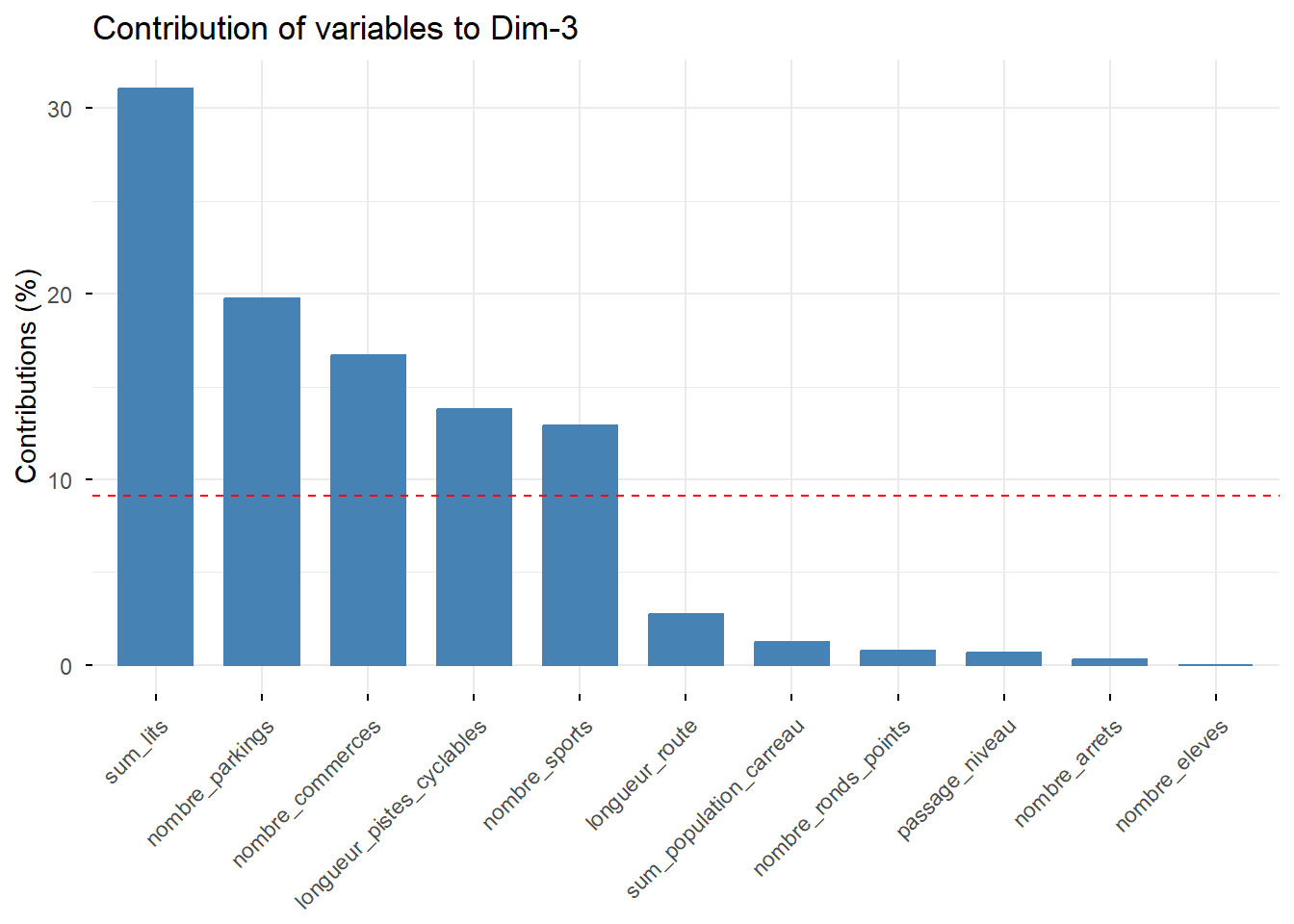
8 - Classification ascendante hiérarchique et cartographie
# CAH sur les scores des individus de l'ACP ----
hc <- HCPC(PCA, nb.clust = 3, graph = FALSE)
# Visualiser les dendrogrammes
fviz_dend(hc, cex = 0.5)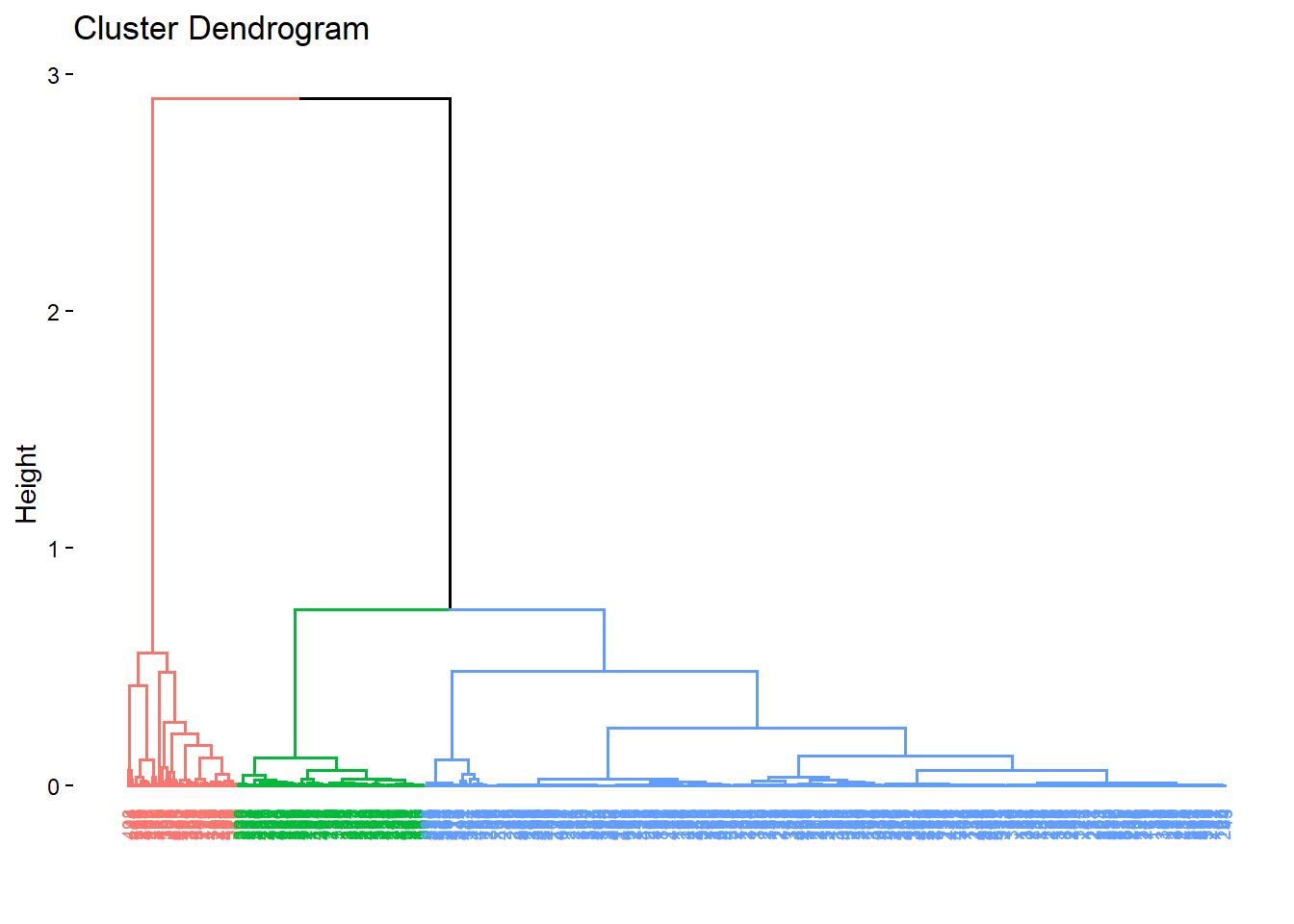
# Visualiser les individus dans le plan factoriel avec une indication de leur cluster
fviz_cluster(hc, geom = "point")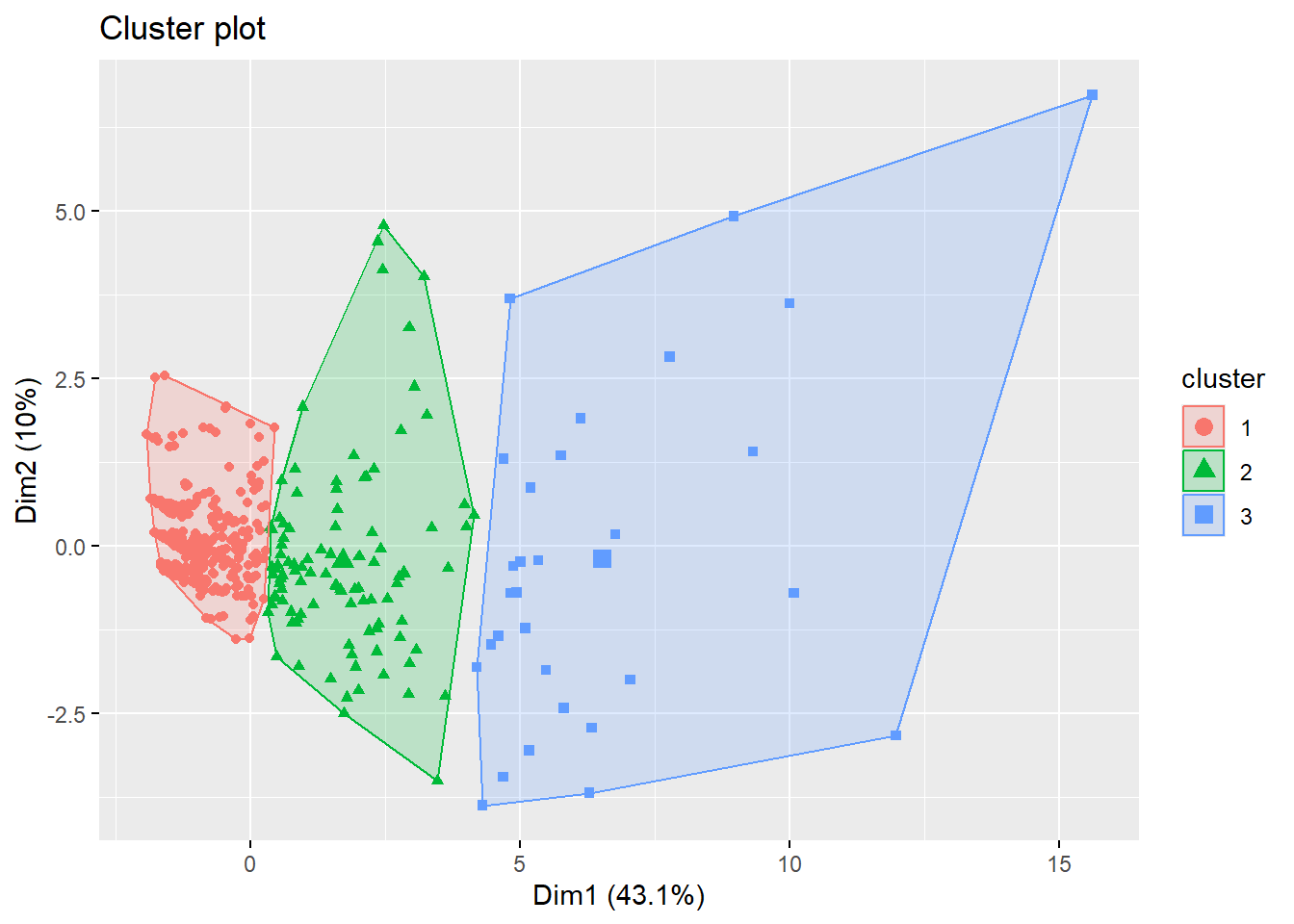
# Extraction des clusters attribués à chaque observation
clusters <- hc$data.clust$clust
length(clusters)## [1] 498# Assurez-vous que vos données originales ont un identifiant unique pour chaque observation
# Ajouter les affectations de cluster à vos données originales
nrow(all_data_filter)## [1] 498## ℹ tmap modes "plot" - "view"tm_basemap(c(leaflet::providers$Esri.WorldTopoMap,
leaflet::providers$OpenStreetMap,
leaflet::providers$Esri.WorldImageryiders,
leaflet::providers$GeoportailFrance.orthos)) +
tm_shape(all_data_filter) +
tm_dots(col = "cluster", palette = "Set1", title = "Cluster") +
tm_basemap(server = "OpenStreetMap") +
tm_layout(legend.position = c("left", "bottom"))##
## ── tmap v3 code detected ───────────────────────────────────────────────────────
## [v3->v4] `tm_tm_dots()`: migrate the argument(s) related to the scale of the
## visual variable `fill` namely 'palette' (rename to 'values') to fill.scale =
## tm_scale(<HERE>).[tm_dots()] Argument `title` unknown.[cols4all] color palettes: use palettes from the R package cols4all. Run
## `cols4all::c4a_gui()` to explore them. The old palette name "Set1" is named
## "brewer.set1"9 - BOXPLOTS
donnees_longues <- tidyr::pivot_longer(all_data_filter,
cols = c(
# sum_population,
# sum_population_active,
sum_lits,
longueur_route,
# nb_intersections,
# reseau_pedestre,
longueur_pistes_cyclables,
nombre_arrets,
nombre_parkings,
nombre_commerces,
# nombre_sante,
# nombre_loisirs,
# nombre_restauration,
nombre_sports,
nombre_ronds_points,
nombre_eleves,
# ZA,
passage_niveau,
sum_population_carreau,
PNR_OK),
names_to = "Variable",
values_to = "Valeur")ggplot(donnees_longues, aes(x = as.factor(cluster), y = Valeur, fill = as.factor(cluster))) +
geom_boxplot() +
facet_wrap(~ Variable, scales = "free_y") + # Crée un panel pour chaque variable
labs(x = "Cluster", y = "Valeur") +
scale_fill_brewer(palette = "Pastel1") + # Utiliser une palette de couleurs
theme_minimal() +
theme(legend.title = element_blank(), axis.text.x = element_text(angle = 45, hjust = 1)) # Personnalise le graphique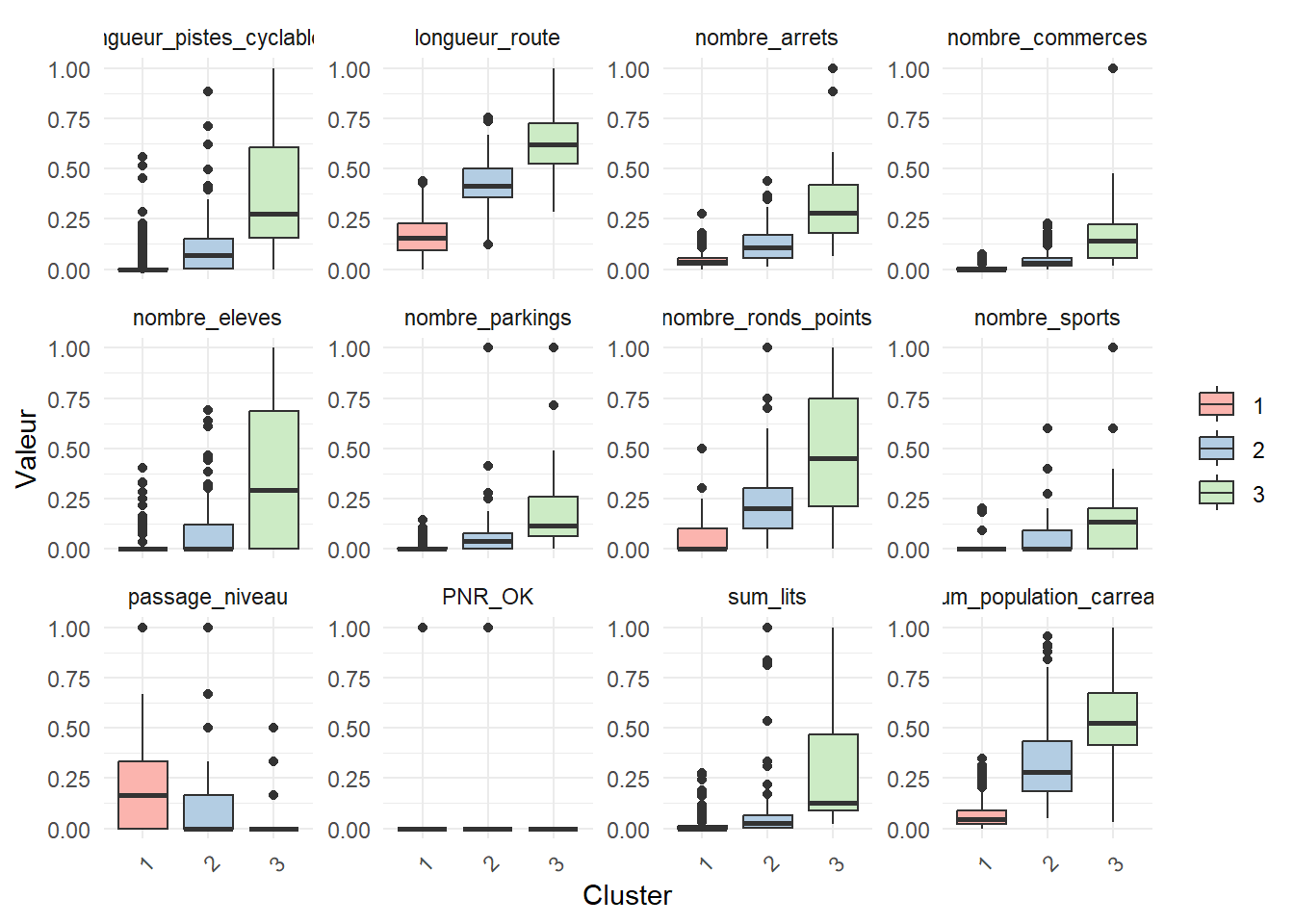
CORRELATION
Corrélation entre les variables dépendantes
# Chargement des données
all_data<- sf::st_read('processed_data/all_data_standardized_stpol_foot_10min_pop_carreau_20240307.gpkg')## Reading layer `all_data_standardized_rennes_stpol_10min_pop_carreau_20240307' from data source `C:\docs\rprojects\database_sf\processed_data\all_data_standardized_stpol_foot_10min_pop_carreau_20240307.gpkg'
## using driver `GPKG'
## Simple feature collection with 140 features and 23 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 603303 ymin: 7019253 xmax: 683443.5 ymax: 7048245
## Projected CRS: RGF93 v1 / Lambert-93## [1] "pk" "ID_number"
## [3] "sum_population" "sum_population_active"
## [5] "sum_lits" "longueur_route"
## [7] "nb_intersections" "reseau_pedestre"
## [9] "longueur_pistes_cyclables" "nombre_arrets"
## [11] "nombre_parkings" "nombre_commerces"
## [13] "nombre_sante" "nombre_loisirs"
## [15] "nombre_restauration" "nombre_sports"
## [17] "nombre_ronds_points" "nombre_eleves"
## [19] "ZA" "passage_niveau"
## [21] "sum_population_carreau" "total_sum"
## [23] "total_sum_allegee" "geom"data_select <- all_data %>%
select(sum_population,
sum_population_carreau,
sum_population_active,
sum_lits,
longueur_route,
nb_intersections,
reseau_pedestre,
longueur_pistes_cyclables,
nombre_arrets,
nombre_parkings,
nombre_commerces,
nombre_sante,
nombre_loisirs,
nombre_restauration,
nombre_sports,
nombre_ronds_points,
nombre_eleves,
ZA,
passage_niveau
) %>%
st_drop_geometry()Coefficient de corrélation
Ci-dessous avec la méthode de Pearson (méthode par défaut). La
corrélation de Pearson est appropriée pour des données continues et
normalement distribuées, mesurant les relations linéaires.
Elle mesure le degré de relation linéaire entre deux variables
quantitatives. En d’autres termes, elle cherche à déterminer si, lorsque
l’une des variables augmente ou diminue, l’autre variable tend également
à augmenter ou diminuer selon un modèle prévisible et constant, ce qui
serait caractéristique d’une relation linéaire. Un coefficient de
corrélation proche de 1 ou -1 indique une forte relation linéaire,
tandis qu’un coefficient proche de 0 suggère une faible ou aucune
relation linéaire.
La formule pour calculer le coefficient de corrélation de Pearson, \(r\), entre deux variables \(X\) et \(Y\) est :
\[ r = \frac{\sum (X_i - \overline{X})(Y_i - \overline{Y})}{\sqrt{\sum (X_i - \overline{X})^2 \sum (Y_i - \overline{Y})^2}} \]
Où: - \(X_i\) et \(Y_i\) sont les valeurs individuelles des
variables \(X\) et \(Y\),
- \(\overline{X}\) et \(\overline{Y}\) sont les moyennes de \(X\) et \(Y\),
Matrice de corrélation
mcor <- cor(data_select,
use = "complete.obs",
method = 'pearson')
corrplot::corrplot(mcor,
type="upper",
order="hclust",
tl.col="black")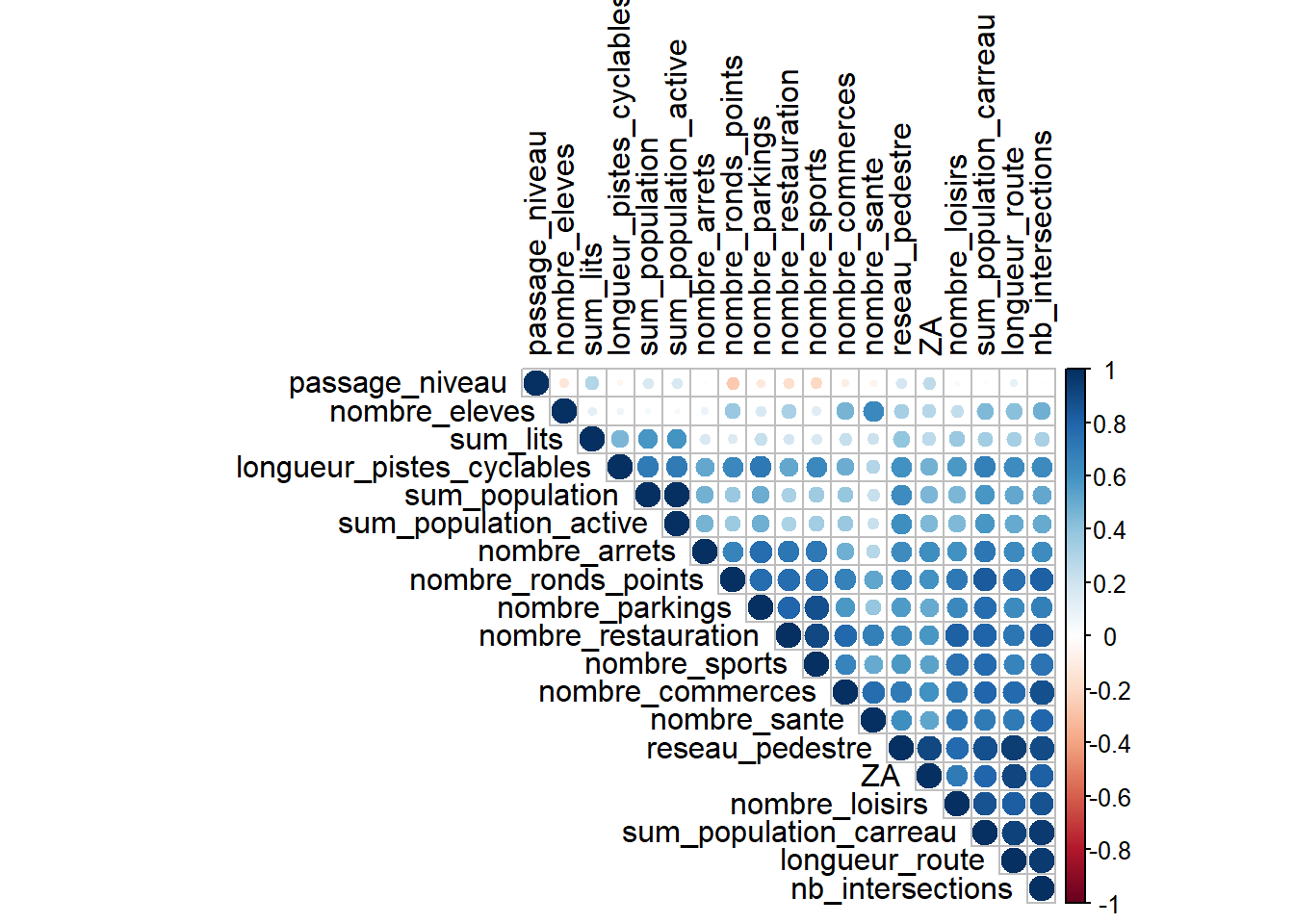
La méthode de Spearman est une mesure de corrélation de rang qui peuvent
être plus appropriées pour des données non normales ou pour des
relations non linéaires.
mcor <- cor(data_select,
use = "complete.obs",
method = 'spearman')
corrplot::corrplot(mcor,
type="upper",
order="hclust",
tl.col="black")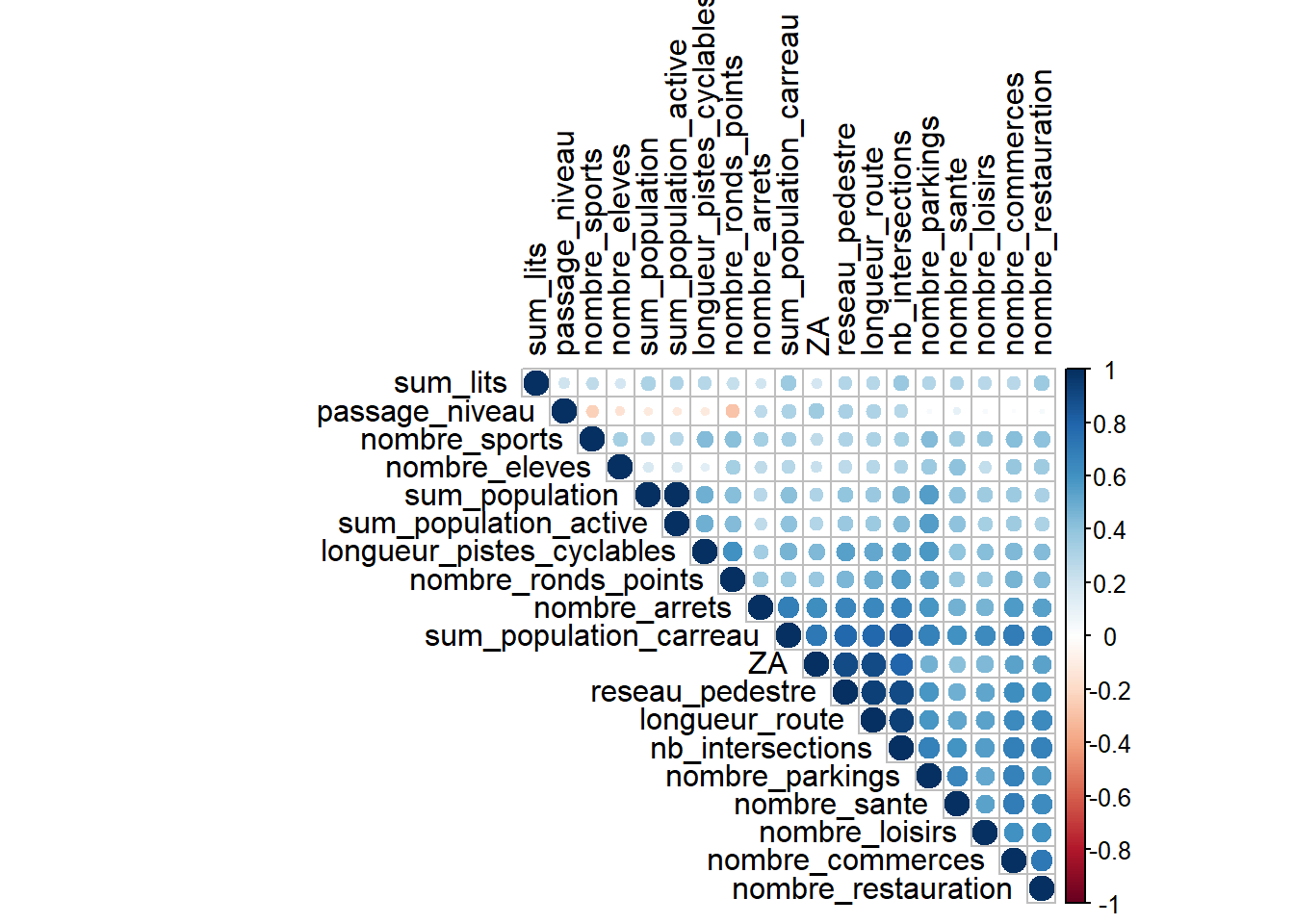
Approche pour Réduire les Variables
Nous commençons par identifier les variables qui ont des corrélations très élevées avec d’autres, pour réduire la redondance.
Fortes Corrélations
Des corrélations très élevées (proches de 1 ou -1) entre deux variables
suggèrent une redondance potentielle. Par exemple,
sum_population et
sum_population_active ont une corrélation de presque 1,
ce qui indique une possible redondance entre ces deux variables. Si une
variable est fortement corrélée avec plusieurs autres variables, cela
peut indiquer qu’elle n’apporte pas d’informations uniques à l’ensemble
de données. Dans notre cas, certaines variables comme
longueur_route et nb_intersections ont
des corrélations élevées avec plusieurs autres variables, suggérant
qu’elles partagent des informations communes.
Variables à Considérer pour Réduction
Variables avec faible corrélation avec les autres : Par exemple,
passage_niveau montre des corrélations très faibles ou
négatives avec la plupart des autres variables, ce qui peut suggérer
qu’elle est moins liée à l’ensemble des variables étudiées.
Nous souhaitons maintenir une diversité en incluant des variables
représentant différents aspects de l’urbanisme et des services, comme
par exemple le nombre de stuctures touristiques ou le nombre de
commerces. Ainsi, nous conservons :
- Population totale : Pour représenter la démographie
- Nombre de structures de tourisme : Pour évaluer l’accès aux soins
espaces de loisirs
- Les arrêts de transport en commun : Reflète l’accessibilité et la
qualité de l’infrastructure de transport public, un facteur important
pour la mobilité urbaine et périurbaine
- Nombre de commerces : Pour refléter l’activité économique
locale
- Nombre d’élèves : Donne une idée de la population scolaire,
pertinent pour évaluer les besoins en éducation et les dynamiques
jeunesse du territoire
- Le nombre de passage à niveau : Signe de l’interconnexion entre le
réseau ferroviaire et la trame urbaine, important pour comprendre les
enjeux de mobilité et de sécurité
- Les zones artificialisées : Pour mesurer le potentiel urbain
- La pente (dans les données sur le vélo) : Évaluation de la difficulté de déplacement en vélo, un aspect fondamental pour promouvoir la mobilité douce et planifier des infrastructures cyclables adaptées
Tableau 1 : Liste des variables sélectionnées
Variance inflation factor (VIF)
Le VIF quantifie combien la variance des coefficients de régression est augmentée en raison de la colinéarité. Il est utilisé pour détecter la multicolinéarité entre plusieurs variables indépendantes.
Il permet de détecter si 2 valeurs contiennent les mêmes informations. Si c’est le cas, il est possible de n’en conserver qu’une seule pour limiter la colinéarité et son influence sur la variance totale.
L’équation du Variance Inflation Factor (VIF) est donnée par :
\[ \text{VIF}_i = \frac{1}{1 - R_i^2} \]
où :
- \(\text{VIF}_i\) est le Variance
Inflation Factor pour le \(i\)-ème
prédicteur.
- \(R_i^2\) est le coefficient de
détermination obtenu en régressant le \(i\)-ème prédicteur sur tous les autres
prédicteurs du modèle.
Cette équation montre que le VIF mesure l’inflation de la variance d’un coefficient de régression en raison de la colinéarité entre les prédicteurs.
ACP
Rappel sur l’ACP.
L’analyse multivariée permet d’étudier les relations entre plusieurs variables et dispose de plusieurs outils statistiques.
Les analyses factorielles font partie de ces
outils.
4 grands types peuvent être utilisés :
* l’analyse en composantes principales (ACP) : L’ACP est utile face à
des variables quantitatives
* l’analyse factorielle des correspondances (AFC) : L’AFC est utile face
à deux variables qualitatives
* l’analyse des correspondances multiples (ACM) : L’ACM est utile face à
plusieurs variables qualitatives
* l’analyse factorielle des correspondances mixtes ou des données mixtes
(AFCM ou AFDM) : L’AFCM prend en compte à la fois des variables
quantitatives et qualitatives
Ainsi, l’analyse en composantes principales (ACP) permet de résumer l’information de plusieurs variables quantitatives. L’information est résumée en un plus petit nombre de “composantes”, qui sont des combinaisons des variables initiales. Les composantes obtenues sont non-corrélées entre elles.
Pour réaliser l’ACP nous utilisons la méthode du package
FactomineR.
Nous utilisons également le package factoextra pour la représentation
graphique.
# Packages
pacman::p_load(sf, dplyr, FactoMineR, factoextra)
# Data
all_data<- sf::st_read('processed_data/all_data_standardized_stpol_foot_10min_pop_carreau_20240307.gpkg')## Reading layer `all_data_standardized_rennes_stpol_10min_pop_carreau_20240307' from data source `C:\docs\rprojects\database_sf\processed_data\all_data_standardized_stpol_foot_10min_pop_carreau_20240307.gpkg'
## using driver `GPKG'
## Simple feature collection with 140 features and 23 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 603303 ymin: 7019253 xmax: 683443.5 ymax: 7048245
## Projected CRS: RGF93 v1 / Lambert-93## [1] "pk" "ID_number"
## [3] "sum_population" "sum_population_active"
## [5] "sum_lits" "longueur_route"
## [7] "nb_intersections" "reseau_pedestre"
## [9] "longueur_pistes_cyclables" "nombre_arrets"
## [11] "nombre_parkings" "nombre_commerces"
## [13] "nombre_sante" "nombre_loisirs"
## [15] "nombre_restauration" "nombre_sports"
## [17] "nombre_ronds_points" "nombre_eleves"
## [19] "ZA" "passage_niveau"
## [21] "sum_population_carreau" "total_sum"
## [23] "total_sum_allegee" "geom"data_select <- all_data %>%
select(sum_population,
sum_population_active,
sum_lits,
longueur_route,
nb_intersections,
reseau_pedestre,
longueur_pistes_cyclables,
nombre_arrets,
nombre_parkings,
nombre_commerces,
nombre_sante,
nombre_loisirs,
nombre_restauration,
nombre_sports,
nombre_ronds_points,
nombre_eleves,
passage_niveau,
ZA) %>%
st_drop_geometry()
glimpse(data_select)## Rows: 140
## Columns: 18
## $ sum_population <dbl> 2.3485879, 2.5887191, 2.7566048, 0.3531290, …
## $ sum_population_active <dbl> 2.3243714, 2.5589343, 2.7410136, 0.3871755, …
## $ sum_lits <dbl> 0.8932275, 0.8932275, 0.8932275, -0.5848741,…
## $ longueur_route <dbl> 5.16867646, 3.10459511, 0.06961055, 1.458407…
## $ nb_intersections <dbl> 5.09987535, 3.42890606, -0.02617106, 0.70487…
## $ reseau_pedestre <dbl> 4.44733819, 2.50619176, 0.36621457, 2.893083…
## $ longueur_pistes_cyclables <dbl> 5.19569185, 4.72415850, -0.29324894, 0.09455…
## $ nombre_arrets <dbl> 7.4673409, 1.9713200, 0.9566700, 0.4493450, …
## $ nombre_parkings <dbl> 7.5419708169, 3.8195204239, -0.2836575398, -…
## $ nombre_commerces <dbl> 3.18472950, 4.82192214, -0.36252123, -0.0896…
## $ nombre_sante <dbl> 1.44786385, 1.74377763, -0.32761883, -0.3276…
## $ nombre_loisirs <dbl> 6.76906609, 2.27561302, -0.42045882, 0.47823…
## $ nombre_restauration <dbl> 7.05862493, 1.84712880, -0.12964559, -0.1296…
## $ nombre_sports <dbl> 7.8168892, 3.8082281, -0.2004331, -0.2004331…
## $ nombre_ronds_points <dbl> 7.6031051, 3.6313338, -0.3404375, 0.4539167,…
## $ nombre_eleves <dbl> -0.1493615, -0.1493615, -0.1493615, -0.14936…
## $ passage_niveau <dbl> -1.16291821, -1.16291821, -0.07024338, -1.16…
## $ ZA <dbl> 4.9050264, 1.9417255, 0.1296123, 1.9693857, …## sum_population sum_population_active sum_lits
## sum_population 1.00000000 0.99924452 0.5893858
## sum_population_active 0.99924452 1.00000000 0.5970567
## sum_lits 0.58938584 0.59705672 1.0000000
## longueur_route 0.51595721 0.50934369 0.3310645
## nb_intersections 0.51573488 0.50758990 0.3248075
## reseau_pedestre 0.62251289 0.61586826 0.3986321
## longueur_pistes_cyclables 0.70085972 0.70353524 0.4589517
## nombre_arrets 0.47642887 0.46292631 0.1609571
## nombre_parkings 0.49372272 0.48691829 0.2361889
## nombre_commerces 0.38658626 0.37958365 0.2340942
## nombre_sante 0.22815439 0.22261811 0.2101464
## nombre_loisirs 0.45276620 0.44955265 0.3741853
## nombre_restauration 0.32226623 0.31477453 0.1898868
## nombre_sports 0.35619350 0.34890209 0.1642547
## nombre_ronds_points 0.37215636 0.36386084 0.1575403
## nombre_eleves 0.04594885 0.04200966 0.1126870
## passage_niveau 0.16093168 0.16483300 0.2967487
## ZA 0.45497554 0.44913702 0.2675785
## longueur_route nb_intersections reseau_pedestre
## sum_population 0.5159572 0.51573488 0.6225129
## sum_population_active 0.5093437 0.50758990 0.6158683
## sum_lits 0.3310645 0.32480750 0.3986321
## longueur_route 1.0000000 0.95834529 0.9458683
## nb_intersections 0.9583453 1.00000000 0.8974281
## reseau_pedestre 0.9458683 0.89742806 1.0000000
## longueur_pistes_cyclables 0.6212782 0.63533071 0.6099911
## nombre_arrets 0.6304407 0.62809750 0.6204415
## nombre_parkings 0.6341161 0.68834338 0.5679835
## nombre_commerces 0.7716204 0.87746876 0.7013466
## nombre_sante 0.7011284 0.79875708 0.6151281
## nombre_loisirs 0.8290609 0.86222682 0.7788058
## nombre_restauration 0.7261066 0.81896695 0.6320947
## nombre_sports 0.6691651 0.73713722 0.5762619
## nombre_ronds_points 0.7597996 0.81215974 0.6631809
## nombre_eleves 0.4103867 0.48575463 0.3354086
## passage_niveau 0.1012891 -0.01765514 0.1825102
## ZA 0.9159476 0.81378985 0.9086366
## longueur_pistes_cyclables nombre_arrets
## sum_population 0.70085972 0.47642887
## sum_population_active 0.70353524 0.46292631
## sum_lits 0.45895172 0.16095714
## longueur_route 0.62127818 0.63044065
## nb_intersections 0.63533071 0.62809750
## reseau_pedestre 0.60999105 0.62044148
## longueur_pistes_cyclables 1.00000000 0.51133285
## nombre_arrets 0.51133285 1.00000000
## nombre_parkings 0.71988456 0.76494600
## nombre_commerces 0.49315849 0.48574788
## nombre_sante 0.29697118 0.28795712
## nombre_loisirs 0.57522343 0.60002434
## nombre_restauration 0.51976910 0.72124036
## nombre_sports 0.64206793 0.71983990
## nombre_ronds_points 0.64625057 0.66965777
## nombre_eleves 0.07767039 0.08170547
## passage_niveau -0.05436620 0.01982639
## ZA 0.47726480 0.61615733
## nombre_parkings nombre_commerces nombre_sante
## sum_population 0.4937227 0.38658626 0.22815439
## sum_population_active 0.4869183 0.37958365 0.22261811
## sum_lits 0.2361889 0.23409417 0.21014637
## longueur_route 0.6341161 0.77162043 0.70112840
## nb_intersections 0.6883434 0.87746876 0.79875708
## reseau_pedestre 0.5679835 0.70134662 0.61512812
## longueur_pistes_cyclables 0.7198846 0.49315849 0.29697118
## nombre_arrets 0.7649460 0.48574788 0.28795712
## nombre_parkings 1.0000000 0.57909093 0.38483873
## nombre_commerces 0.5790909 1.00000000 0.76856785
## nombre_sante 0.3848387 0.76856785 1.00000000
## nombre_loisirs 0.6408026 0.72857029 0.71837280
## nombre_restauration 0.7938725 0.78133175 0.68449219
## nombre_sports 0.8707952 0.66652507 0.50563612
## nombre_ronds_points 0.7678163 0.67253213 0.52858386
## nombre_eleves 0.1601140 0.46376846 0.64256178
## passage_niveau -0.1202759 -0.09643249 -0.06504966
## ZA 0.5011603 0.60638970 0.52282748
## nombre_loisirs nombre_restauration nombre_sports
## sum_population 0.45276620 0.3222662 0.3561935
## sum_population_active 0.44955265 0.3147745 0.3489021
## sum_lits 0.37418535 0.1898868 0.1642547
## longueur_route 0.82906090 0.7261066 0.6691651
## nb_intersections 0.86222682 0.8189669 0.7371372
## reseau_pedestre 0.77880583 0.6320947 0.5762619
## longueur_pistes_cyclables 0.57522343 0.5197691 0.6420679
## nombre_arrets 0.60002434 0.7212404 0.7198399
## nombre_parkings 0.64080258 0.7938725 0.8707952
## nombre_commerces 0.72857029 0.7813317 0.6665251
## nombre_sante 0.71837280 0.6844922 0.5056361
## nombre_loisirs 1.00000000 0.8106949 0.7444830
## nombre_restauration 0.81069492 1.0000000 0.9015159
## nombre_sports 0.74448301 0.9015159 1.0000000
## nombre_ronds_points 0.71607979 0.7627560 0.7559842
## nombre_eleves 0.24913984 0.3232247 0.1333694
## passage_niveau -0.03681151 -0.1716293 -0.2032522
## ZA 0.70181504 0.5802376 0.5334793
## nombre_ronds_points nombre_eleves passage_niveau
## sum_population 0.3721564 0.04594885 0.16093168
## sum_population_active 0.3638608 0.04200966 0.16483300
## sum_lits 0.1575403 0.11268697 0.29674871
## longueur_route 0.7597996 0.41038665 0.10128909
## nb_intersections 0.8121597 0.48575463 -0.01765514
## reseau_pedestre 0.6631809 0.33540865 0.18251024
## longueur_pistes_cyclables 0.6462506 0.07767039 -0.05436620
## nombre_arrets 0.6696578 0.08170547 0.01982639
## nombre_parkings 0.7678163 0.16011398 -0.12027588
## nombre_commerces 0.6725321 0.46376846 -0.09643249
## nombre_sante 0.5285839 0.64256178 -0.06504966
## nombre_loisirs 0.7160798 0.24913984 -0.03681151
## nombre_restauration 0.7627560 0.32322473 -0.17162925
## nombre_sports 0.7559842 0.13336940 -0.20325217
## nombre_ronds_points 1.0000000 0.37300188 -0.26137254
## nombre_eleves 0.3730019 1.00000000 -0.13643833
## passage_niveau -0.2613725 -0.13643833 1.00000000
## ZA 0.6054540 0.28288749 0.25267380
## ZA
## sum_population 0.4549755
## sum_population_active 0.4491370
## sum_lits 0.2675785
## longueur_route 0.9159476
## nb_intersections 0.8137899
## reseau_pedestre 0.9086366
## longueur_pistes_cyclables 0.4772648
## nombre_arrets 0.6161573
## nombre_parkings 0.5011603
## nombre_commerces 0.6063897
## nombre_sante 0.5228275
## nombre_loisirs 0.7018150
## nombre_restauration 0.5802376
## nombre_sports 0.5334793
## nombre_ronds_points 0.6054540
## nombre_eleves 0.2828875
## passage_niveau 0.2526738
## ZA 1.0000000## Warning in geom_bar(stat = "identity", fill = barfill, color = barcolor, :
## Ignoring empty aesthetic: `width`.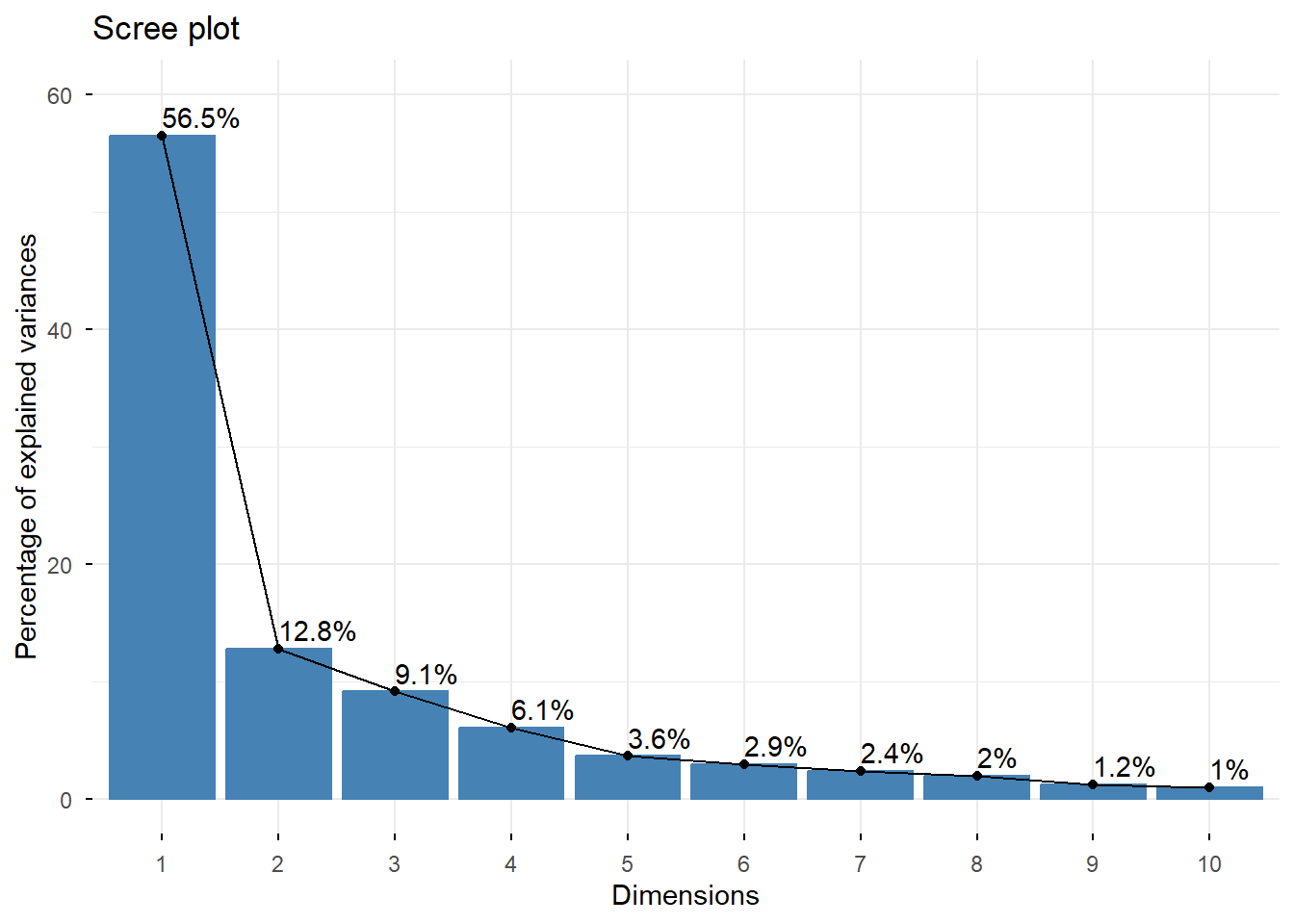
# Cercle des corrélations
fviz_pca_var(PCA, col.var="contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)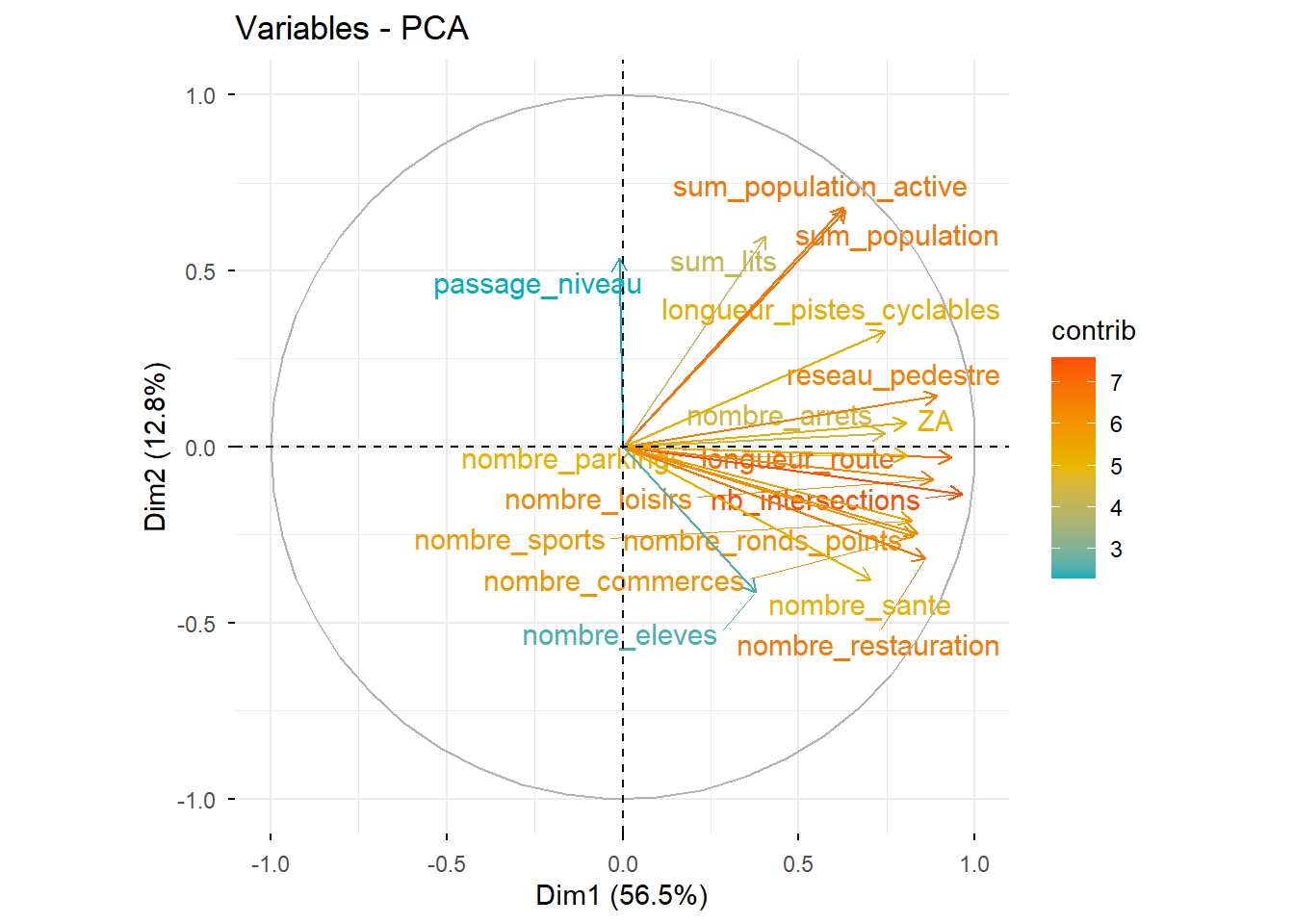
# Graphique des individus
fviz_pca_ind(PCA, col.ind = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)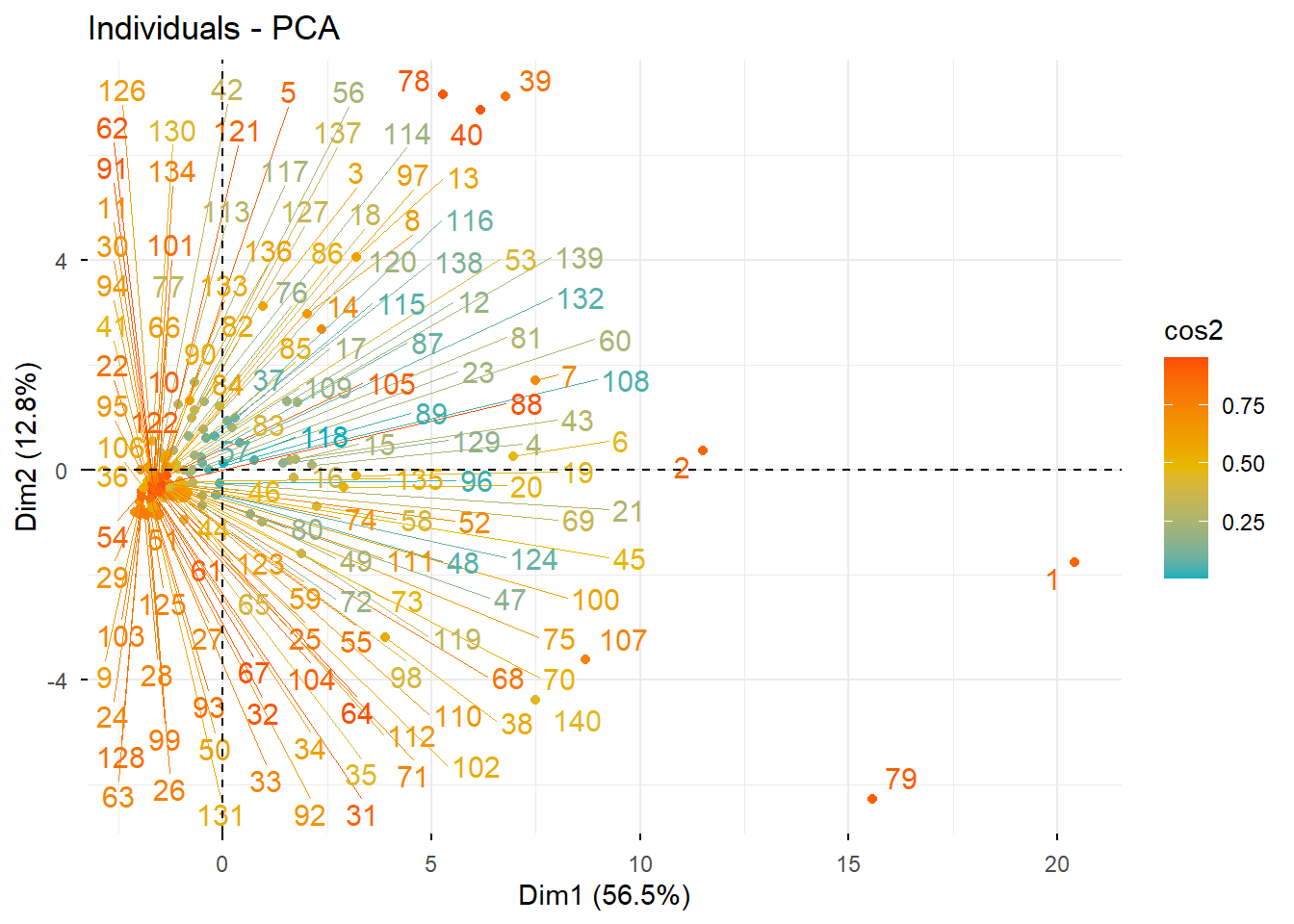
## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 1.017626e+01 56.534764746 56.53476
## comp 2 2.302828e+00 12.793490456 69.32826
## comp 3 1.641325e+00 9.118474164 78.44673
## comp 4 1.090875e+00 6.060418561 84.50715
## comp 5 6.519664e-01 3.622035797 88.12918
## comp 6 5.235041e-01 2.908355903 91.03754
## comp 7 4.289506e-01 2.383059011 93.42060
## comp 8 3.542501e-01 1.968055855 95.38865
## comp 9 2.173461e-01 1.207478567 96.59613
## comp 10 1.777867e-01 0.987703791 97.58384
## comp 11 1.242768e-01 0.690426904 98.27426
## comp 12 8.632486e-02 0.479582561 98.75385
## comp 13 8.363086e-02 0.464615896 99.21846
## comp 14 5.444949e-02 0.302497162 99.52096
## comp 15 4.806500e-02 0.267027772 99.78799
## comp 16 2.873946e-02 0.159663652 99.94765
## comp 17 8.957709e-03 0.049765050 99.99742
## comp 18 4.651475e-04 0.002584153 100.00000# Contribution de chaque variable aux trois premiers axes
fviz_contrib(PCA, choice = "var", axes = 1) # axe 1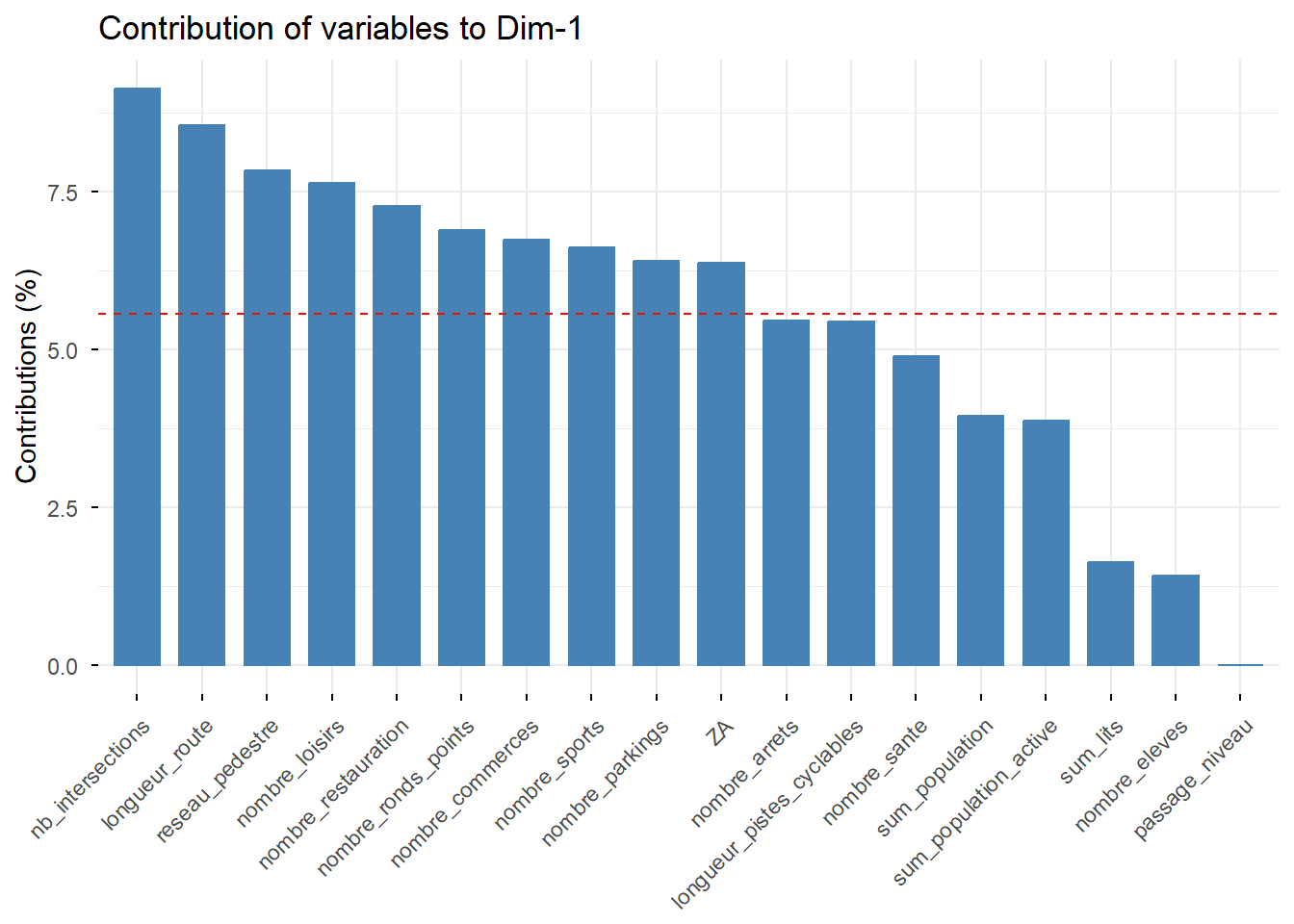
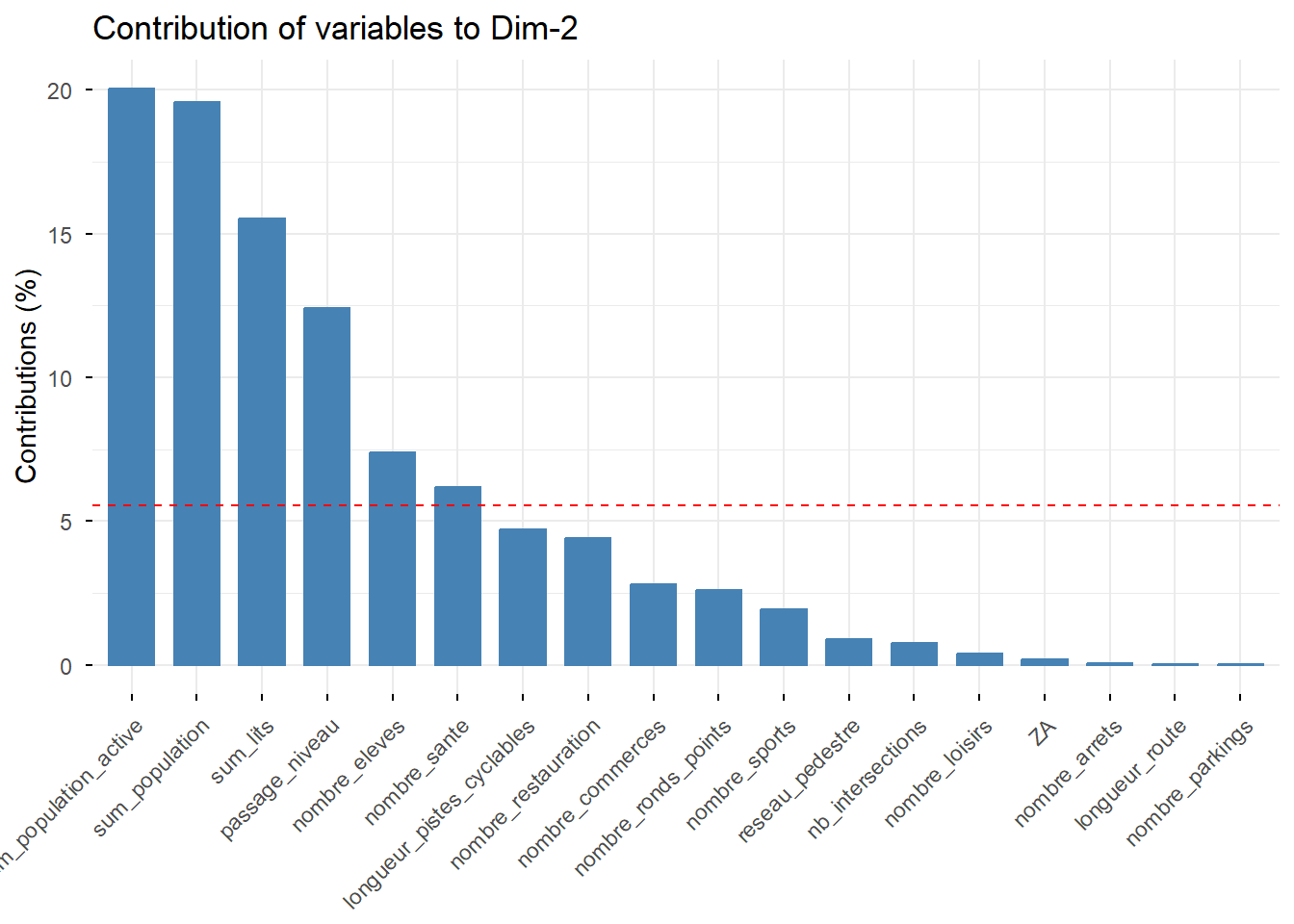
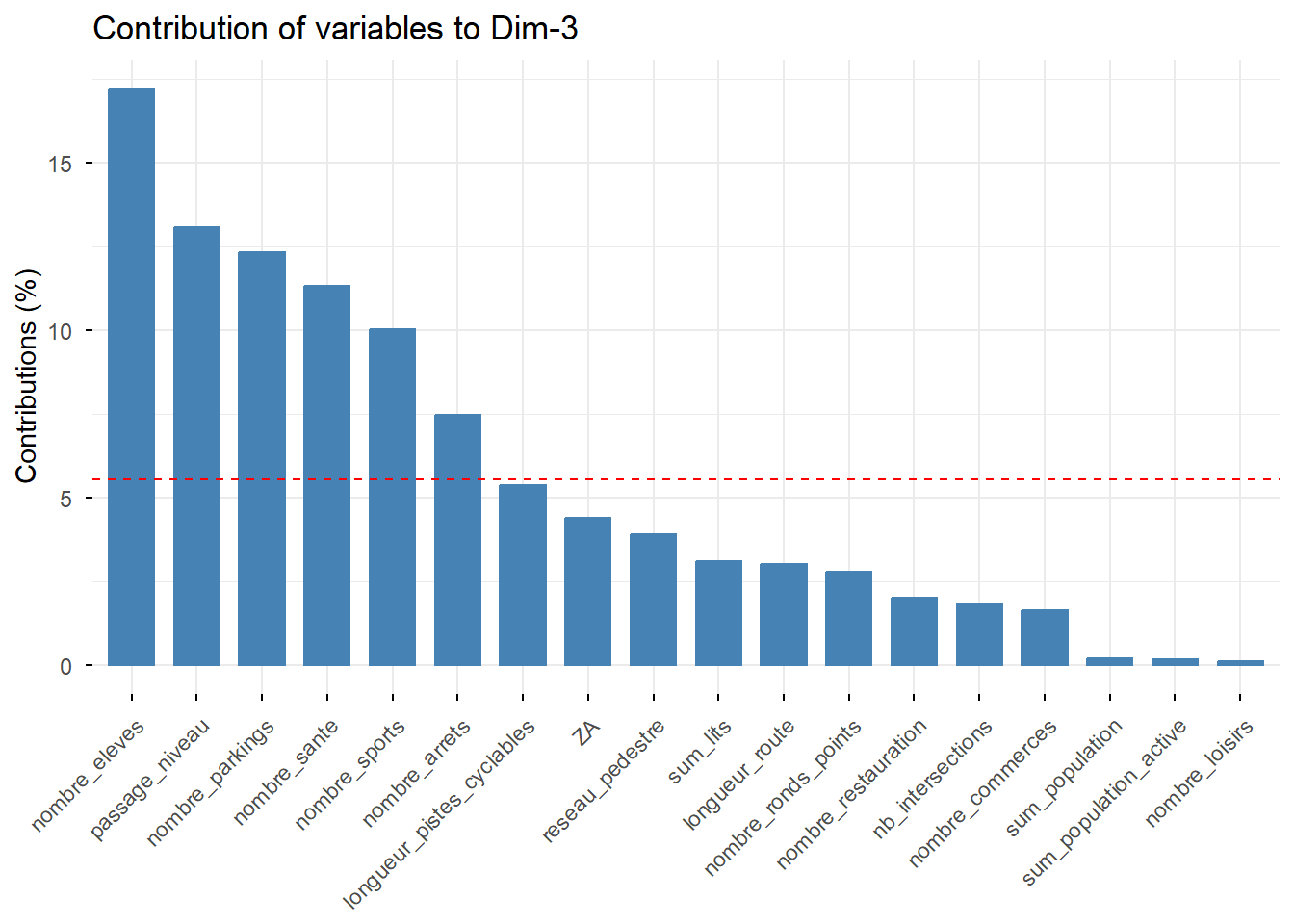
# Contribution de chaque individu aux deux premiers axes
fviz_contrib(PCA, choice = "ind", axes = 1)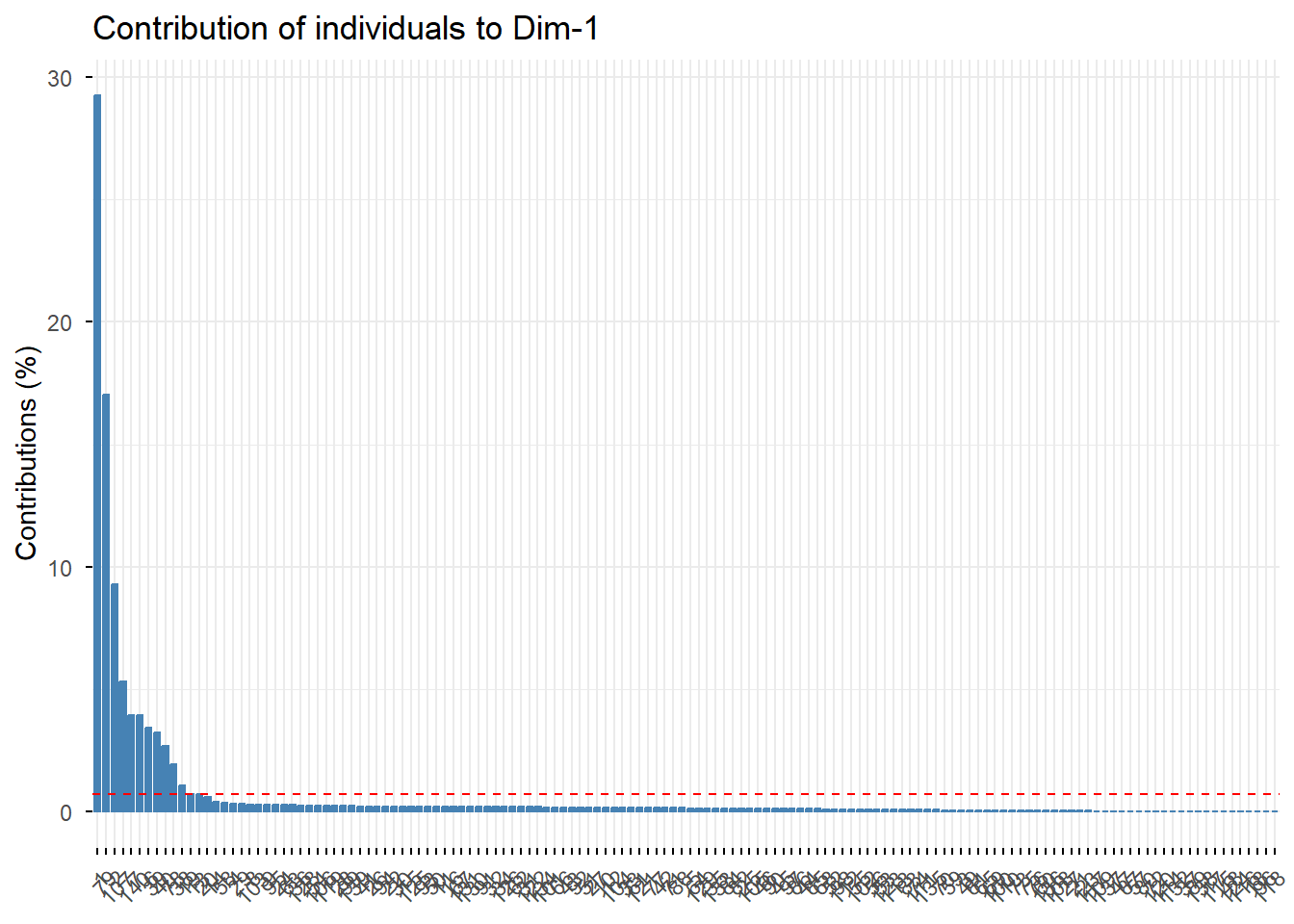
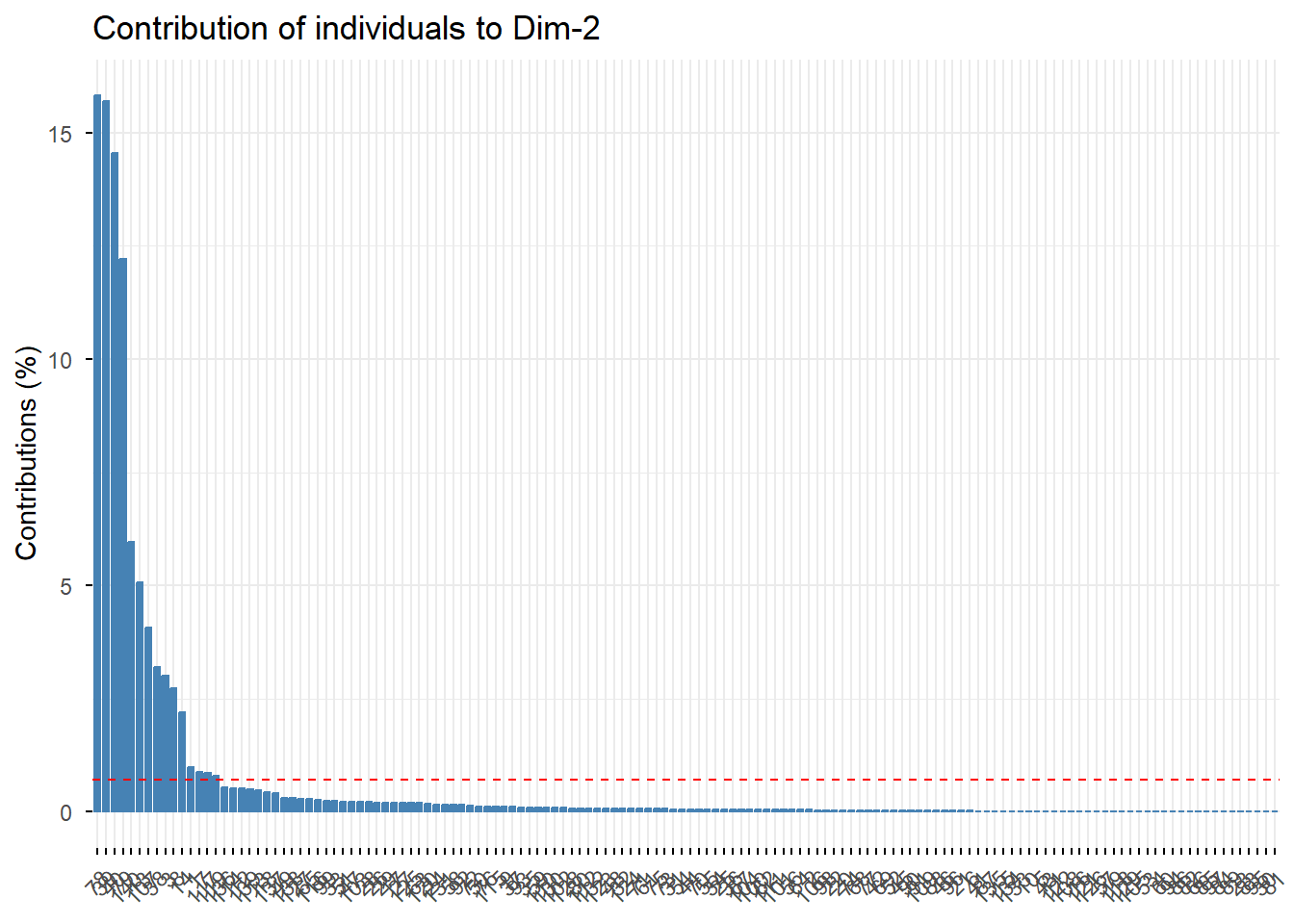
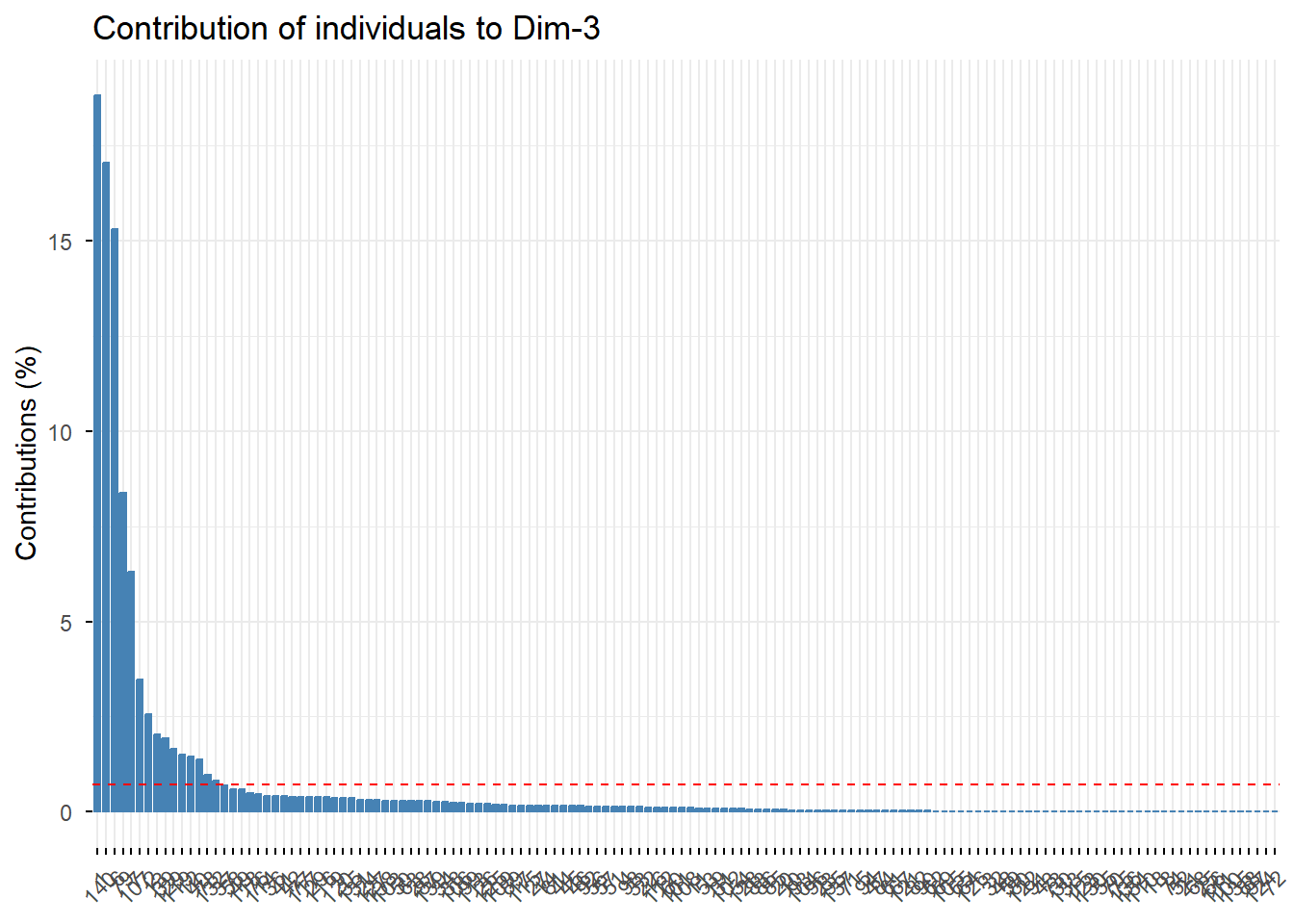
MULTINIVEAUX
Variables étudiées par niveau
NIVEAU 2 : lignes de train avec :
* nombre d’arrêts
* temps moyen du trajet entre la gare de départ et la gare d’arrivée *
longueur de la ligne
* nombre de trains par jour, à partir des données GTFS
* nombre d’incidents ? à partir de quelle base ?
NIVEAU 1 : gares avec :
* population à 10 minutes en voiture ? * infos tourisme
* arrêts de transport à proximité à 10 minutes à pied ? * commerces à 10
minutes à pied ?
* nombre d’élèves à 10 minutes à vélo ?
* zones artificielles à 10 minutes à pied ?
* passages à niveau à 10 minutes à pied ?
TABLEAU DES LIGNES FERROVIAIRES (niveau 2)
Ici je calcule le temps moyen d’un trajet entre la gare de départ et
la gare d’arrivée. Je compte également le nombre d’arrêts par
ligne.
# temps moyen pour toutes les lignes ----
# Charger les données
## Itinéraires de transport en commun. Ex : Paris Montparnasse - Toulouse Matabiau
routes <- read.csv('data/GTFS/export-ter-gtfs-last/routes.txt', header = TRUE) %>%
filter(route_type == 2) # 0 = Tram/Tramway/Train léger ; # 1 = Métro ; 2 = Rails ; 3 = Bus ; 4 = Ferry
## Trajets pour chaque ligne.
## Un trajet est une séquence de deux arrêts ou plus qui se produisent pendant une période de temps spécifique
trips <- read.csv('data/GTFS/export-ter-gtfs-last/trips.txt', header = TRUE)
## Les heures d'arrivée et de départ d'un véhicule aux arrêts pour chaque trajet.
stop_times <- read.csv('data/GTFS/export-ter-gtfs-last/stop_times.txt', header = TRUE)
# dataframe pour stocker les durées moyennes par route entre point de départ et d'arrivée
average_durations <- data.frame(route_id = character(),
average_time = numeric())
# Boucle sur chaque route_id dans routes
for(route_id_select in unique(as.character(routes$route_id))) {
# Filtre les trajets pour la route actuelle
filtered_trips <- trips %>%
filter(route_id == route_id_select)
# Extraction du nom de la route
routes_filter <- filtered_trips$route_id[1]
route_long_name <- routes %>%
filter(route_id == routes_filter)
route_long_name <- route_long_name$route_long_name
# Filtre les stop_times pour les trajets filtrés
stop_times_filtered <- stop_times %>%
filter(trip_id %in% filtered_trips$trip_id) %>%
arrange(trip_id, arrival_time) %>%
select(trip_id, stop_id, arrival_time, departure_time)
# Calculer la durée de chaque voyage
trip_durations <- stop_times_filtered %>%
group_by(trip_id) %>%
summarise(
start_time = first(departure_time),
end_time = last(arrival_time),
duration = as.numeric(hms(end_time) - hms(start_time), units = "mins")
)
# Calcule la durée moyenne pour la route actuelle
average_duration <- trip_durations %>%
summarise(average_time = mean(duration, na.rm = TRUE))
# Ajout du résultat dans le dataframe des durées moyennes
average_durations <- rbind(average_durations, data.frame(route_id = route_id_select,
route_name = route_long_name,
average_time = average_duration$average_time))
}
# Affiche les durées moyennes pour toutes les routes
head(average_durations)## route_id
## 1 FR:Line::00F7208C-CEBC-4521-A792-6EC3ABB65811:
## 2 FR:Line::0128E1D5-9183-4D58-B1CF-F5AA5A64A037:
## 3 FR:Line::0202671B-7107-429E-A37B-473C55E0254C:
## 4 FR:Line::022B77D9-D121-4DCB-B808-FB2F7931866B:
## 5 FR:Line::02534A5F-903C-454E-A24F-E6E2E23B3CBF:
## 6 FR:Line::02D330A2-2167-400E-BE91-0B5990BA287B:
## route_name average_time
## 1 Saint-Étienne - Roanne 69.86747
## 2 Marseille - Toulon - Hyeres 73.33628
## 3 Montpellier Saint-Roch - Avignon Centre 70.95122
## 4 Nantes Cholet Angers Saumur 44.59722
## 5 Ambérieu - Mâcon 48.98058
## 6 Nantes - Clisson 27.69841# nombre de stops par lignes (routes) ----
# Charger les données
## Itinéraires de transport en commun. Ex : Paris Montparnasse - Toulouse Matabiau
routes <- read.csv('data/GTFS/export-ter-gtfs-last/routes.txt', header = TRUE) %>%
filter(route_type == 2) # 0 = Tram/Tramway/Train léger ; # 1 = Métro ; 2 = Rails ; 3 = Bus ; 4 = Ferry
## Trajets pour chaque ligne
## Un trajet est une séquence de deux arrêts ou plus qui se produisent pendant une période de temps spécifique
trips <- read.csv('data/GTFS/export-ter-gtfs-last/trips.txt', header = TRUE)
## Arrêts où les véhicules prennent ou déposent les usagers.
## Définit également les stations et les entrées de station.
stops <- read.csv('data/GTFS/export-ter-gtfs-last/stops.txt', header = TRUE)
# Joindre trips à routes
trips_with_routes <- trips %>%
inner_join(routes, by = "route_id")
# Joindre stop_times à trips_with_routes
stops_with_routes <- stop_times %>%
inner_join(trips_with_routes, by = "trip_id")
stops_per_route <- stops_with_routes %>%
group_by(route_id) %>%
summarise(number_of_stops = n_distinct(stop_id))
head(stops_per_route)## # A tibble: 6 × 2
## route_id number_of_stops
## <chr> <int>
## 1 FR:Line::00F7208C-CEBC-4521-A792-6EC3ABB65811: 15
## 2 FR:Line::0128E1D5-9183-4D58-B1CF-F5AA5A64A037: 19
## 3 FR:Line::0202671B-7107-429E-A37B-473C55E0254C: 23
## 4 FR:Line::022B77D9-D121-4DCB-B808-FB2F7931866B: 12
## 5 FR:Line::02534A5F-903C-454E-A24F-E6E2E23B3CBF: 25
## 6 FR:Line::02D330A2-2167-400E-BE91-0B5990BA287B: 8# Fusion des deux data frames sur la colonne 'route_id'
merged_data <- merge(average_durations, stops_per_route, by = "route_id")
# Affichage des premières lignes du data frame fusionné
head(merged_data)## route_id
## 1 FR:Line::00F7208C-CEBC-4521-A792-6EC3ABB65811:
## 2 FR:Line::0128E1D5-9183-4D58-B1CF-F5AA5A64A037:
## 3 FR:Line::0202671B-7107-429E-A37B-473C55E0254C:
## 4 FR:Line::022B77D9-D121-4DCB-B808-FB2F7931866B:
## 5 FR:Line::02534A5F-903C-454E-A24F-E6E2E23B3CBF:
## 6 FR:Line::02D330A2-2167-400E-BE91-0B5990BA287B:
## route_name average_time number_of_stops
## 1 Saint-Étienne - Roanne 69.86747 15
## 2 Marseille - Toulon - Hyeres 73.33628 19
## 3 Montpellier Saint-Roch - Avignon Centre 70.95122 23
## 4 Nantes Cholet Angers Saumur 44.59722 12
## 5 Ambérieu - Mâcon 48.98058 25
## 6 Nantes - Clisson 27.69841 8## [1] "route_id" "route_name" "average_time" "number_of_stops"Point étape : ici j’ai donc les lignes avec leur temps moyen de trajet entre le départ et l’arrivée et le nombre d’arrêts pour chaque trajet.
TABLEAU DES GARES (niveau 1)
# création du tableau route_id, stops_id, stop_name ----
stops <- read.csv('data/GTFS/export-ter-gtfs-last/stops.txt', header = TRUE)
stop_times <- read.csv('data/GTFS/export-ter-gtfs-last/stop_times.txt', header = TRUE)
trips <- read.csv('data/GTFS/export-ter-gtfs-last/trips.txt', header = TRUE)
routes <- read.csv('data/GTFS/export-ter-gtfs-last/routes.txt', header = TRUE)
# Joindre les data frames sur 'stop_id'
joined_data <- merge(stop_times, stops, by = "stop_id")
# final_table <- joined_data %>%
# group_by(trip_id) %>%
# summarise(
# trip_id = paste(unique(trip_id), collapse = ", "),
# stops_name = paste(unique(stop_name), collapse = ", ")
# )
# Joindre les data frames sur 'trip_id'
joined_data_2 <- merge(trips, joined_data, by = "trip_id")
# final_table_2 <- joined_data_2 %>%
# group_by(trip_id) %>%
# summarise(
# trip_id = paste(unique(trip_id), collapse = ", "),
# route_id = paste(unique(route_id), collapse = ", ")
# )
# Joindre les data frames sur 'stop_id'
joined_data_3 <- merge(routes, joined_data_2, by = "route_id")
final_table <- joined_data_3 %>%
group_by(stop_id) %>%
summarise(
stop_id = paste(unique(stop_id), collapse = ", "),
route_id = paste(unique(route_id), collapse = ", "),
stop_name = paste(unique(stop_name), collapse = ", ")
)
final_table_filter <- final_table %>%
filter(grepl('Train', stop_id))Ici je recupère les ID des routes avec les ID des arrêts et leurs noms
## # A tibble: 6 × 3
## stop_id route_id stop_name
## <chr> <chr> <chr>
## 1 StopPoint:OCETrain TER-71793150 FR:Line::21B4B826-2492-4170-AC04-0B… Portbou
## 2 StopPoint:OCETrain TER-80142893 FR:Line::7BA6A09D-4D2A-4474-992B-81… Appenwei…
## 3 StopPoint:OCETrain TER-80142901 FR:Line::7BA6A09D-4D2A-4474-992B-81… Legelshu…
## 4 StopPoint:OCETrain TER-80142919 FR:Line::7BA6A09D-4D2A-4474-992B-81… Kork
## 5 StopPoint:OCETrain TER-80142927 FR:Line::7BA6A09D-4D2A-4474-992B-81… Kehl
## 6 StopPoint:OCETrain TER-80143099 FR:Line::7BA6A09D-4D2A-4474-992B-81… Offenburg# Chargement des data
# mes données sur les gares : calculs de variables pour des isoshrones 15 minutes à pied sur les 400 gares des Hauts-de-France
gares_HDF <- sf::st_read('processed_data/gares_HDR_join_region_HDF_foot_p15_20240214.gpkg')## Reading layer `gares_HDR_join_region_HDF_foot_p15_20240214' from data source
## `C:\docs\rprojects\database_sf\processed_data\gares_HDR_join_region_HDF_foot_p15_20240214.gpkg'
## using driver `GPKG'
## Simple feature collection with 393 features and 27 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 595141.4 ymin: 6874373 xmax: 781232.5 ymax: 7108435
## Projected CRS: RGF93 v1 / Lambert-93gares_HDF <- gares_HDF %>%
rename(stop_name = ID_number)
gares_HDF_merge <- merge(gares_HDF, final_table_filter, by = "stop_name")
names(gares_HDF_merge)## [1] "stop_name" "voy_2022"
## [3] "ID" "NOM_M"
## [5] "NOM" "INSEE_REG"
## [7] "ID_number_old" "sum_population"
## [9] "sum_population_active" "sum_lits"
## [11] "longueur_route" "nb_intersections"
## [13] "reseau_pedestre" "longueur_pistes_cyclables"
## [15] "superficie_vegetation" "nombre_arrets"
## [17] "nombre_parkings" "nombre_commerces"
## [19] "nombre_sante" "nombre_loisirs"
## [21] "nombre_restauration" "nombre_sports"
## [23] "nombre_ronds_points" "nombre_eleves"
## [25] "superficie_iso" "ZA"
## [27] "passage_niveau" "stop_id"
## [29] "route_id" "geom"gares_HDF_merge_select <- gares_HDF_merge %>%
dplyr::select(stop_name,voy_2022,sum_population,sum_lits,nombre_arrets,
nombre_commerces, nombre_eleves, ZA, passage_niveau, stop_id, route_id)
head(gares_HDF_merge_select)## Simple feature collection with 6 features and 11 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 611500.6 ymin: 6932087 xmax: 766005.6 ymax: 7003747
## Projected CRS: RGF93 v1 / Lambert-93
## stop_name voy_2022 sum_population sum_lits nombre_arrets nombre_commerces
## 1 Abancourt 71517 1122 0 23 0
## 2 Abbeville 841557 22895 171 9 66
## 3 Achiet 80648 1281 0 19 2
## 4 Albert 524871 9814 360 20 28
## 5 Amiens 6004673 137790 1796 79 94
## 6 Amifontaine 15468 390 0 9 0
## nombre_eleves ZA passage_niveau stop_id
## 1 0 960423.8 4 StopPoint:OCETrain TER-87313759
## 2 0 1387238.6 0 StopPoint:OCETrain TER-87317362
## 3 0 1455085.8 0 StopPoint:OCETrain TER-87342048
## 4 678 1611076.5 0 StopPoint:OCETrain TER-87313072
## 5 4109 1867851.2 0 StopPoint:OCETrain TER-87313874
## 6 0 1058629.1 0 StopPoint:OCETrain TER-87171744
## route_id
## 1 FR:Line::7BDE293E-0D29-48A4-8978-8ADB3FFEA340:, FR:Line::A16522A1-3A9D-406B-B7AB-12E318E7CC92:, FR:Line::A8CBE20D-E000-4EEC-A4EE-F928AD249687:, FR:Line::B2E5B266-DAE7-4C0A-ABA0-B46411FB2CAA:, FR:Line::C6FA7EBE-4D15-41AC-AAFC-6B62BA46E49E:, FR:Line::DD461A4B-557A-4303-B639-AED4F7A5141B:, FR:Line::E0C5BF51-53A3-4542-B417-3AFE4D5EA545:
## 2 FR:Line::4B0DFE2B-138B-455F-BCEF-0B57A660A95F:, FR:Line::965C0279-4764-4FEA-B29B-363968EA28CE:, FR:Line::cf0d9ce8-bf4e-448e-8bf0-6c965a95c788:, FR:Line::D77B2111-D576-48D5-878E-5D6C094D611A:
## 3 FR:Line::7BB51D2B-5268-45E9-AEEE-1F1053DE381C:, FR:Line::7BDE293E-0D29-48A4-8978-8ADB3FFEA340:, FR:Line::B2E5B266-DAE7-4C0A-ABA0-B46411FB2CAA:, FR:Line::E597DAD9-42BF-4927-BEDB-0B05091BCBBE:
## 4 FR:Line::7BB51D2B-5268-45E9-AEEE-1F1053DE381C:, FR:Line::7BDE293E-0D29-48A4-8978-8ADB3FFEA340:, FR:Line::B2E5B266-DAE7-4C0A-ABA0-B46411FB2CAA:, FR:Line::D77B2111-D576-48D5-878E-5D6C094D611A:, FR:Line::E597DAD9-42BF-4927-BEDB-0B05091BCBBE:
## 5 FR:Line::4B0DFE2B-138B-455F-BCEF-0B57A660A95F:, FR:Line::53D6728B-4D88-418C-823F-F3E5B975E9D6:, FR:Line::74E36C89-DC6A-4CE9-A1C7-CC8552AE882C:, FR:Line::7BB51D2B-5268-45E9-AEEE-1F1053DE381C:, FR:Line::7BDE293E-0D29-48A4-8978-8ADB3FFEA340:, FR:Line::8519D738-1A3F-477E-A18B-116B8863F0F8:, FR:Line::965C0279-4764-4FEA-B29B-363968EA28CE:, FR:Line::9F35A2B3-4B24-4076-A960-83E359C90C1D:, FR:Line::A8CBE20D-E000-4EEC-A4EE-F928AD249687:, FR:Line::B2E5B266-DAE7-4C0A-ABA0-B46411FB2CAA:, FR:Line::BA37A6D8-F8EA-4672-8077-B6A6CA91A26F:, FR:Line::C6FA7EBE-4D15-41AC-AAFC-6B62BA46E49E:, FR:Line::cf0d9ce8-bf4e-448e-8bf0-6c965a95c788:, FR:Line::D77B2111-D576-48D5-878E-5D6C094D611A:, FR:Line::DD461A4B-557A-4303-B639-AED4F7A5141B:, FR:Line::E27CA8B0-68E6-43FB-BE1B-B0388CDA1008:, FR:Line::E597DAD9-42BF-4927-BEDB-0B05091BCBBE:
## 6 FR:Line::93676b4d-70bb-42ae-a4ad-fade138a46c4:
## geom
## 1 POINT (611500.6 6954704)
## 2 POINT (615814.8 7001062)
## 3 POINT (684265.1 7003747)
## 4 POINT (674493.3 6989720)
## 5 POINT (650564.5 6977107)
## 6 POINT (766005.6 6932087)## [1] "stop_name" "voy_2022" "sum_population" "sum_lits"
## [5] "nombre_arrets" "nombre_commerces" "nombre_eleves" "ZA"
## [9] "passage_niveau" "stop_id" "route_id" "geom"ICI je fusionne mes données avec le tableaux GTFS des stop name
# Fusion des tableaux de niveau 1 et 2 ----
gares_HDF_merge_select_fusion <- merge(gares_HDF_merge_select,
merged_data,
by = 'route_id')
head(gares_HDF_merge_select_fusion)## Simple feature collection with 6 features and 14 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 682055.4 ymin: 7002663 xmax: 767913 ymax: 7049370
## Projected CRS: RGF93 v1 / Lambert-93
## route_id stop_name voy_2022
## 1 FR:Line::11D73E7F-3314-4000-B93A-A4781C56C041: Leval 2955
## 2 FR:Line::11D73E7F-3314-4000-B93A-A4781C56C041: Avesnelles 4532
## 3 FR:Line::11D73E7F-3314-4000-B93A-A4781C56C041: Dompierre 1695
## 4 FR:Line::11D73E7F-3314-4000-B93A-A4781C56C041: Saint-Hilaire 21
## 5 FR:Line::18E717A0-950C-40A2-8F27-98A8EE8ADD20: Cuinchy 34787
## 6 FR:Line::18E717A0-950C-40A2-8F27-98A8EE8ADD20: Salomé 10248
## sum_population sum_lits nombre_arrets nombre_commerces nombre_eleves
## 1 11304 0 10 0 0
## 2 6823 25 10 2 565
## 3 1690 0 10 0 0
## 4 4990 0 6 0 0
## 5 9077 13 60 3 0
## 6 6612 0 45 1 0
## ZA passage_niveau stop_id
## 1 1190081.9 4 StopPoint:OCETrain TER-87295790
## 2 1333134.5 1 StopPoint:OCETrain TER-87295725
## 3 912603.3 0 StopPoint:OCETrain TER-87295774
## 4 918654.4 1 StopPoint:OCETrain TER-87297531
## 5 1622946.6 1 StopPoint:OCETrain TER-87342410
## 6 993264.7 1 StopPoint:OCETrain TER-87342451
## route_name average_time number_of_stops
## 1 Aulnoye - Aymeries - Hirson 41.94118 14
## 2 Aulnoye - Aymeries - Hirson 41.94118 14
## 3 Aulnoye - Aymeries - Hirson 41.94118 14
## 4 Aulnoye - Aymeries - Hirson 41.94118 14
## 5 Lille Flandres - Don-Sainghin - Béthune 61.02632 18
## 6 Lille Flandres - Don-Sainghin - Béthune 61.02632 18
## geom
## 1 POINT (759823.6 7009919)
## 2 POINT (767913 7002663)
## 3 POINT (762334.8 7005671)
## 4 POINT (765420.2 7004128)
## 5 POINT (682055.4 7047216)
## 6 POINT (688399.3 7049370)Je fusionne le tableau du niveau 1 des gares (gares_HDF_merge_select) et du niveau 2 des lignes (merged_data)
MODELE MULTINIVEAUX
Je souhaite comprendre les variables qui influencent le nombre de voyageurs des gares en 2022.
# modèle multi-niveaux
# Modèle de régression multiniveaux
model <- lme4::lmer(voy_2022 ~ scale(sum_population) + scale(sum_lits) + scale(nombre_arrets) + scale(nombre_commerces) + scale(nombre_eleves) + scale(ZA) + scale(passage_niveau) + scale(average_time) + scale(number_of_stops) +
(1 | route_id), # prise en compte des variables des routes comme point de départ avant même de prendre en compte les variables sur les gares
data = gares_HDF_merge_select_fusion)
# Afficher le résumé du modèle
summary(model)## Linear mixed model fit by REML ['lmerMod']
## Formula:
## voy_2022 ~ scale(sum_population) + scale(sum_lits) + scale(nombre_arrets) +
## scale(nombre_commerces) + scale(nombre_eleves) + scale(ZA) +
## scale(passage_niveau) + scale(average_time) + scale(number_of_stops) +
## (1 | route_id)
## Data: gares_HDF_merge_select_fusion
##
## REML criterion at convergence: 2211
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.2513 -0.3671 -0.0971 0.1829 6.0432
##
## Random effects:
## Groups Name Variance Std.Dev.
## route_id (Intercept) 2.299e+09 47947
## Residual 4.103e+09 64056
## Number of obs: 96, groups: route_id, 30
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 36624 11345 3.228
## scale(sum_population) -77130 53273 -1.448
## scale(sum_lits) 58208 52656 1.105
## scale(nombre_arrets) -7389 10183 -0.726
## scale(nombre_commerces) 22045 11692 1.885
## scale(nombre_eleves) -14341 9507 -1.508
## scale(ZA) 28886 10383 2.782
## scale(passage_niveau) 6547 7852 0.834
## scale(average_time) 21063 13856 1.520
## scale(number_of_stops) -12582 12978 -0.969
##
## Correlation of Fixed Effects:
## (Intr) scl(sm_p) scl(sm_l) scl(nmbr_r) scl(nmbr_c) scl(nmbr_l)
## scl(sm_ppl) -0.009
## scl(sm_lts) 0.013 -0.984
## scl(nmbr_r) 0.017 -0.164 0.166
## scl(nmbr_c) 0.021 0.195 -0.263 -0.208
## scl(nmbr_l) -0.006 -0.201 0.241 -0.012 -0.478
## scale(ZA) -0.017 -0.269 0.256 -0.164 -0.354 -0.060
## scl(pssg_n) -0.009 0.034 0.006 -0.121 0.012 0.074
## scl(vrg_tm) 0.045 0.100 -0.082 0.104 0.053 0.018
## scl(nmbr__) 0.015 0.053 -0.042 0.064 -0.039 0.014
## sc(ZA) scl(p_) scl(v_)
## scl(sm_ppl)
## scl(sm_lts)
## scl(nmbr_r)
## scl(nmbr_c)
## scl(nmbr_l)
## scale(ZA)
## scl(pssg_n) -0.139
## scl(vrg_tm) -0.059 0.081
## scl(nmbr__) -0.046 0.009 -0.467# R2
# Installer et charger le package MuMIn si nécessaire
if (!requireNamespace("MuMIn", quietly = TRUE)) install.packages("MuMIn")## Registered S3 methods overwritten by 'MuMIn':
## method from
## nobs.multinom broom
## nobs.fitdistr broom## R2m R2c
## [1,] 0.181769 0.4755837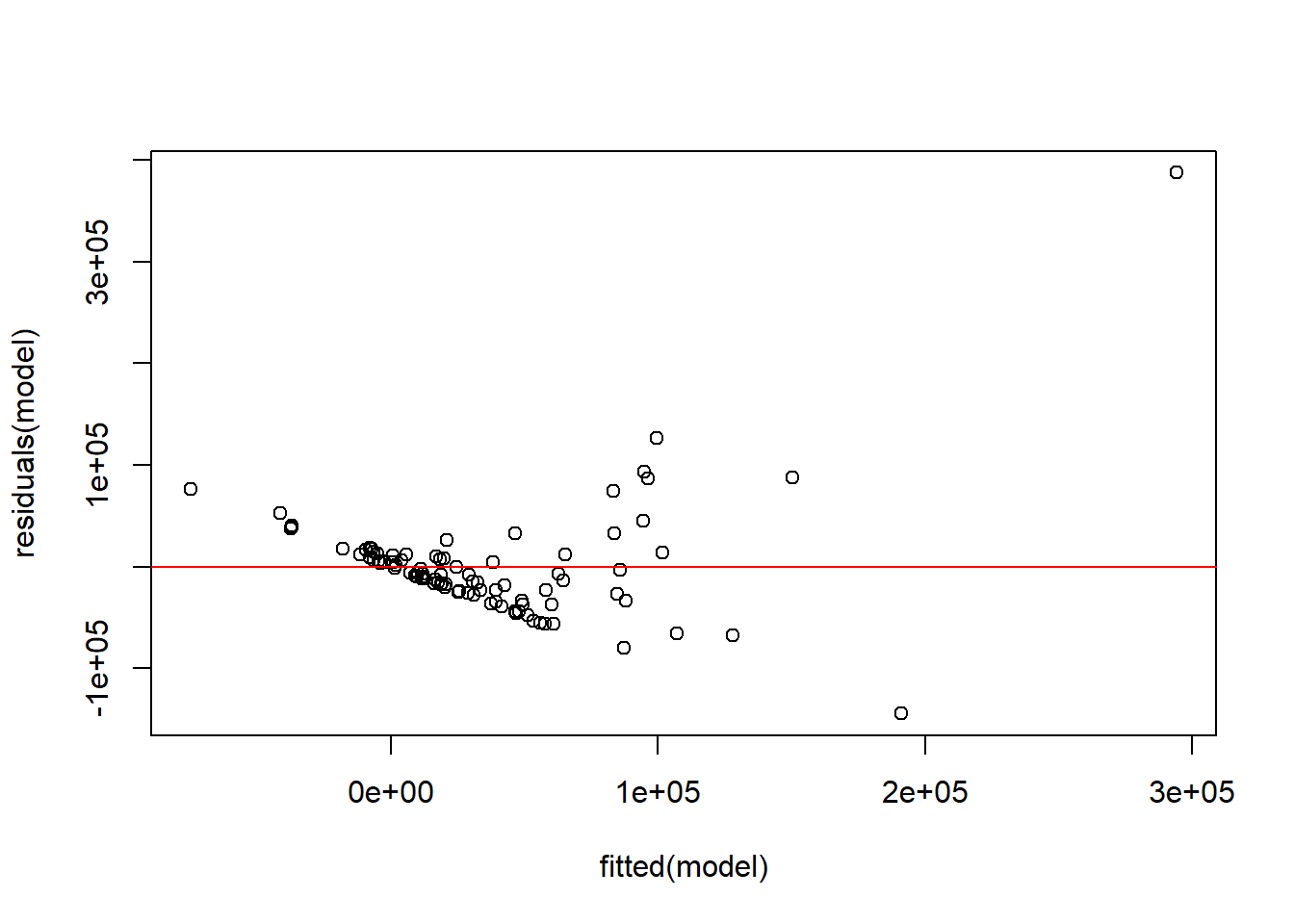
# Histogramme des résidus pour vérifier la normalité
hist(residuals(model), breaks = "Scott", main = "Histogramme des Résidus", xlab = "Résidus")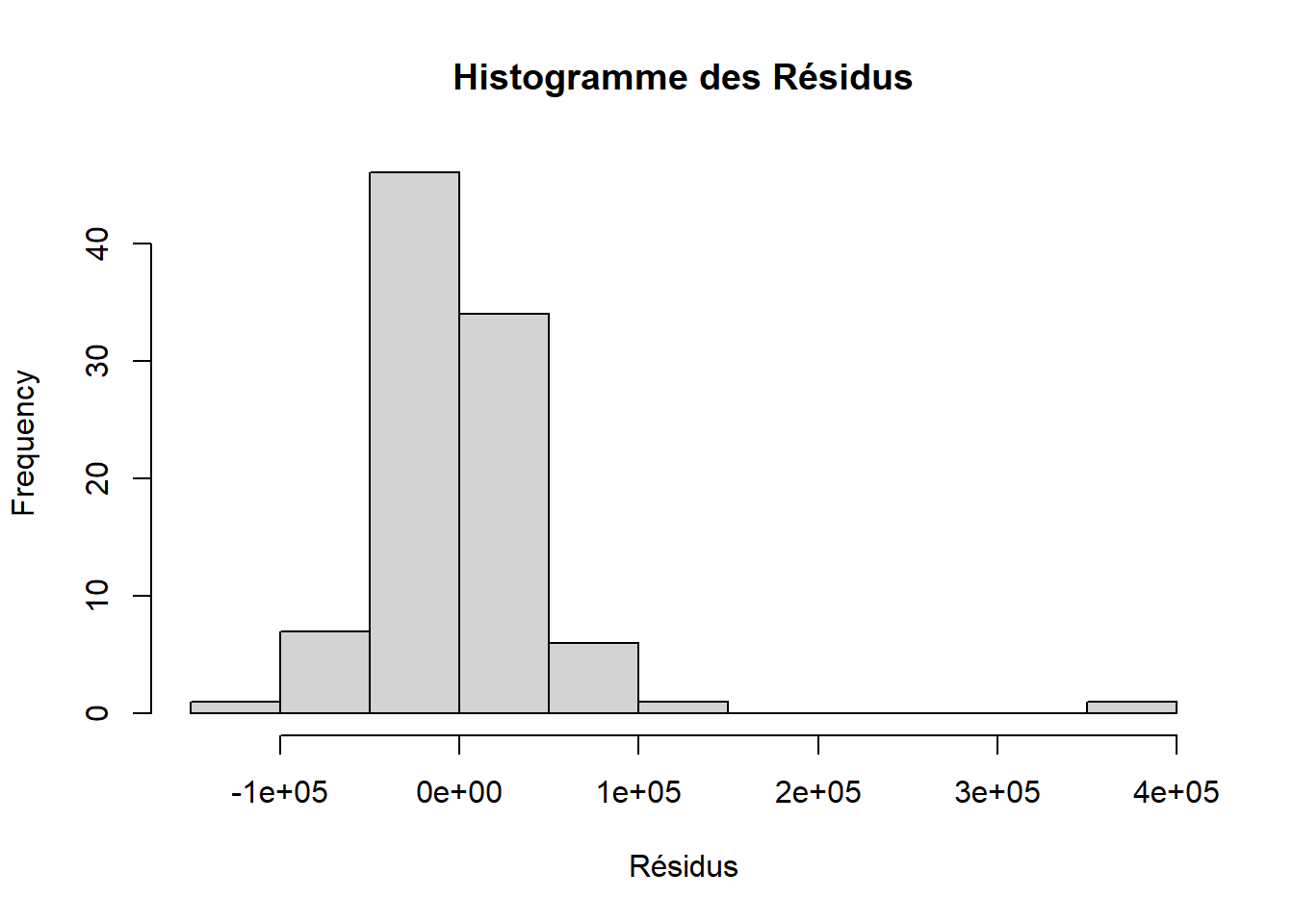
# QQ-plot des résidus
# Dans un QQ-plot, les points devraient se situer approximativement le long de la ligne rouge
# si les résidus suivent une distribution normale.
qqnorm(residuals(model))
qqline(residuals(model), col = "red")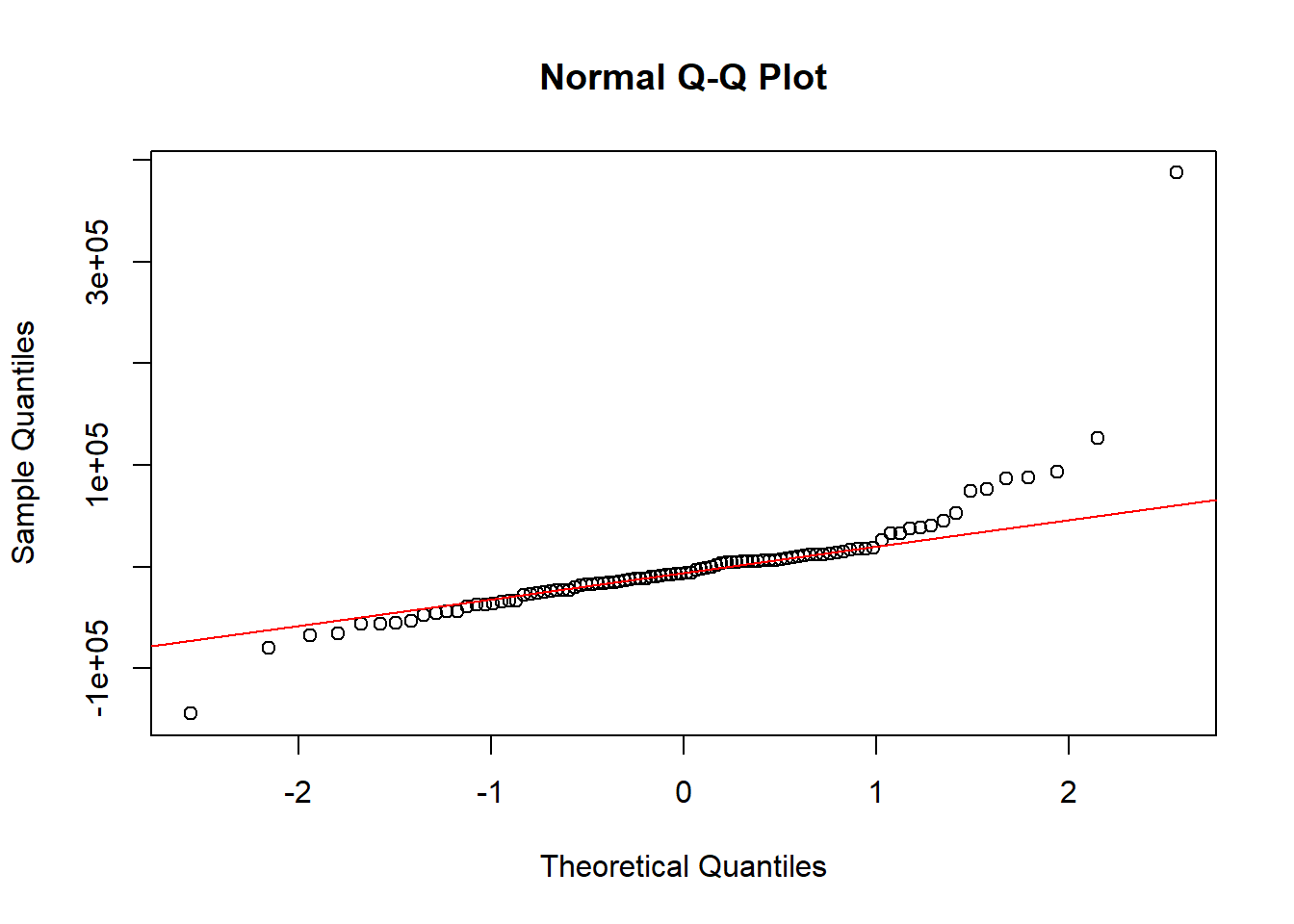
TRANSFORMATION
- La standardisation (scores z) se concentre sur la
reconfiguration des données pour qu’elles aient une moyenne de 0 et un
écart-type de 1, rendant ainsi la distribution des données standardisée
en termes d’unités d’écart-type. Elle est utile pour comparer des scores
entre différentes échelles et est souvent préférée dans les analyses qui
supposent une distribution normale des données.
- La normalisation Min-Max redimensionne les données
dans un intervalle fixe, souvent [0, 1], en ajustant chaque valeur selon
les valeurs minimales et maximales de l’ensemble de données, ce qui est
utile pour les modèles sensibles aux variations d’échelle entre les
variables. Elle est particulièrement utile pour les algorithmes
sensibles aux échelles des variables, comme les algorithmes basés sur
les distances. La normalisation Min-Max est souvent utilisée dans les
contextes où l’uniformité de l’échelle entre les variables est
cruciale.
- La normalisation par la valeur maximale ajuste les
données selon la plus grande valeur absolue de l’ensemble de données,
rendant toutes les valeurs relatives à cette valeur maximale, ce qui est
une approche simplifiée de mise à l’échelle par rapport à une valeur de
référence unique. Elle est similaire à la normalisation Min-Max mais se
concentre uniquement sur le redimensionnement par rapport à la valeur
maximale de chaque variable. Si toutes les valeurs sont positives, les
données varient entre 0 et 1. La normalisation par la valeur maximale
peut être préférée pour sa simplicité et lorsque la dominance de la
valeur maximale est significative pour l’analyse.
LS0tDQp0aXRsZTogIiINCm91dHB1dDogaHRtbF9kb2N1bWVudA0KLS0tDQoNCmBgYHtyIHNldHVwLCBpbmNsdWRlPUZBTFNFfQ0Ka25pdHI6Om9wdHNfY2h1bmskc2V0KGVjaG8gPSBUUlVFLCBvdXQud2lkdGggPSAnMTAwJScpDQpgYGANCg0KIyBBTkFMWVNFUyBURUxMaSB7LnRhYnNldCAudW5udW1iZXJlZH0NCg0KQ2V0dGEgcGFnZSAgYSBwb3VyIGJ1dCBkZSBwcsOpc2VudGVyIHVuIGVuc2VtYmxlIGRlIG3DqXRob2RlcyBkZSBzdGF0aXN0aXF1ZXMgIChjb3Jyw6lsYXRpb24sIEFDUCwgbW9kw6hsZSBkZSByw6lncmVzc2lvbikgDQoNCiMjIEhERi1BVVZfTElNIChtaW5fbWF4KQ0KDQojIyMgMSAtIEFuYWx5c2UgZGVzIGRvbm7DqWVzDQoNCk5vdXMgY2hlcmNob25zIMOgIMOpdHVkaWVyIGxlcyBsaWVucyBlbnRyZSBsYSBmcsOpcXVlbnRhdGlvbiB2b3lhZ2V1cnMgMjAyMiBkZXMgZ2FyZXMgU05DRiBzaXR1w6llcyBkYW5zIGxlcyBIYXV0cy1kZS1GcmFuY2UgKGNhcnRlIDEpIGV0IGRhbnMgbGVzIGFuY2llbm5lcyByw6lnaW9ucyBBdXZlcmduZSBldCBMaW1vdXNpbiAoY2FydGUgMikgYXZlYyB1biBlbnNlbWJsZSBkZSB2YXJpYWJsZXMgcXVhbnRpdGF0aXZlcy4gDQoNCg0KPGJyPg0KDQo8Y2VudGVyPg0KIVtdKGltYWdlcy9jYXJ0ZV9IREYucG5nKQ0KKkNhcnRlIDEgOiBDYXJ0b2dyYXBoaWUgZGVzIGdhcmVzIGRhbnMgbGEgcsOpZ2lvbiBkZXMgSGF1dHMtZGUtRnJhbmNlKg0KPGJyPg0KPC9jZW50ZXI+DQoNCg0KPGNlbnRlcj4NCiFbXShpbWFnZXMvY2FydGVfYXV2X2xpbS5wbmcpDQoqQ2FydGUgMiA6IENhcnRvZ3JhcGhpZSBkZXMgZ2FyZXMgZGVzIGFuY2llbm5lcyByw6lnaW9ucyBBdXZlcmduZSBldCBMaW1vdXNpbioNCjxicj4NCjwvY2VudGVyPg0KDQpgYGB7cn0NCnBhY21hbjo6cF9sb2FkKHNmLCB0bWFwLCBkcGx5ciwgbWFwdmlldywgRmFjdG9NaW5lUiwgZmFjdG9leHRyYSwNCiAgICAgICAgICAgICAgIHBlcmZvcm1hbmNlLCAjIGFuYWx5c2VyIGxlcyBtb2TDqGxlcyBzdGF0aXN0aXF1ZXMNCiAgICAgICAgICAgICAgIGdncGxvdDIsIGRic2NhbiwgYnJvb20uaGVscGVycywgY2FyLCBmYWN0b2V4dHJhLCBjb29ycGxvdA0KICAgICAgICAgICAgICAgKQ0KYGBgDQoNCg0KUG91ciBjZWxhIG5vdXMgZGlzcG9zb25zIGRlcyB2YXJpYWJsZXMgc3VpdmFudGVzLiBDZXMgdmFyaWFibGVzIG9udCDDqXTDqSBjYWxjdWzDqWVzIHBvdXIgY2hhcXVlIGlzb2Nocm9uZSBkZSAqKjEwIG1pbnV0ZXMgw6AgcGllZCoqIGF1dG91ciBkZSBjaGFxdWUgZ2FyZS4NCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJScsIGluY2x1ZGU9VFJVRX0NCmFsbF9kYXRhX2hkZiA8LSBzZjo6c3RfcmVhZCgncHJvY2Vzc2VkX2RhdGEvYWxsX2RhdGFfcmVnaW9uX0hERl9mb290XzEwbWluXzIwMjQwMzE5X21pbl9tYXguZ3BrZycpICU+JSANCiAgZHBseXI6OnNlbGVjdCgtYyhJRCwgcmVzZWF1X3BlZGVzdHJlLCBwb3BfcDE1XzIwMTcpKQ0KbmFtZXMoYWxsX2RhdGFfaGRmKQ0KYWxsX2RhdGFfYXV2X2xpbSA8LSBzZjo6c3RfcmVhZCgncHJvY2Vzc2VkX2RhdGEvYWxsX2RhdGFfcmVnaW9uX0F1dl9MaW1fZm9vdF8xMG1pbl8yMDI0MDMxOV9taW5fbWF4Lmdwa2cnKQ0KbmFtZXMoYWxsX2RhdGFfYXV2X2xpbSkNCmFsbF9kYXRhIDwtIHJiaW5kKGFsbF9kYXRhX2hkZiwgYWxsX2RhdGFfYXV2X2xpbSkNCmBgYA0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCm1hcHZpZXcoYWxsX2RhdGEpDQpgYGANCg0KKipOb21icmUgZGUgdm95YWdldXJzIHRvdGFsKioNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnLCBpbmNsdWRlPVRSVUV9DQpzdW0oYWxsX2RhdGEkdm95XzIwMjIpDQpgYGANCg0KYGBge3IsIGluY2x1ZGU9RiwgZWNobyA9IEZ9DQpnYXJlc19IRFIgPC0gc2Y6OnN0X3JlYWQoJ3Byb2Nlc3NlZF9kYXRhL2dhcmVzX0hEUl9qb2luX3JlZ2lvbl9IREZfZm9vdF8xMG1pbl8yMDI0MDMxNy5ncGtnJykgJT4lIA0KICBkcGx5cjo6c2VsZWN0KGMobm9tX2dhcmUgPSBJRF9udW1iZXIsIA0KICAgICAgICAgICAgICAgICAgdm95XzIwMjIpKQ0KbmFtZXMoZ2FyZXNfSERSKQ0KZ2FyZXNfcmVnaW9uX0F1dl9MaW0gPC0gc2Y6OnN0X3JlYWQoJ3Byb2Nlc3NlZF9kYXRhL2dhcmVzX3JlZ2lvbl9BdXZfTGltX2Zvb3RfcDEwXzIwMjQwMzEzLmdwa2cnKSU+JSANCiAgZHBseXI6OnNlbGVjdChjKG5vbV9nYXJlLCANCiAgICAgICAgICAgICAgICAgIHZveV8yMDIyKSkNCg0KbmFtZXMoZ2FyZXNfcmVnaW9uX0F1dl9MaW0pDQphbGxfZGF0YV9nYXJlcyA8LSByYmluZChnYXJlc19IRFIsIGdhcmVzX3JlZ2lvbl9BdXZfTGltKQ0KbmFtZXMoYWxsX2RhdGFfZ2FyZXMpDQp0b3BfZ2FyZXMgPC0gYWxsX2RhdGFfZ2FyZXMgJT4lIA0KICBhcnJhbmdlKGRlc2Modm95XzIwMjIpKQ0KYGBgDQoNCioqVG9wIDEwIGRlcyBnYXJlcyoqDQoNCmBgYHtyfQ0KdG9wX2dhcmVzWzE6MTAsXQ0KYGBgDQoNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQpnbGltcHNlKGFsbF9kYXRhKQ0KYGBgDQoNCjxicj4NCioqQm94cGxvdHMgZGVzIGRvbm7DqWVzKioNCjxicj4NCg0KYGBge3J9DQpkYXRhX2FsbF9ib3hwbG90IDwtIGFsbF9kYXRhICU+JQ0KICBkcGx5cjo6c2VsZWN0KHN1bV9wb3B1bGF0aW9uLCBzdW1fcG9wdWxhdGlvbl9hY3RpdmUsIHN1bV9saXRzLCBsb25ndWV1cl9yb3V0ZSwNCiAgICAgICAgICAgICAgICBuYl9pbnRlcnNlY3Rpb25zLCBsb25ndWV1cl9waXN0ZXNfY3ljbGFibGVzLA0KICAgICAgICAgICAgICAgIG5vbWJyZV9hcnJldHMsbm9tYnJlX3BhcmtpbmdzLCBub21icmVfY29tbWVyY2VzLG5vbWJyZV9zYW50ZSwNCiAgICAgICAgICAgICAgICBub21icmVfbG9pc2lycywgbm9tYnJlX3Jlc3RhdXJhdGlvbiwgbm9tYnJlX3Nwb3J0cywNCiAgICAgICAgICAgICAgICBub21icmVfcm9uZHNfcG9pbnRzLCBub21icmVfZWxldmVzLCBaQSwgcGFzc2FnZV9uaXZlYXUsDQogICAgICAgICAgICAgICAgc3VtX3BvcHVsYXRpb25fY2FycmVhdSwgUE5SX09LKSAlPiUNCiAgc3RfZHJvcF9nZW9tZXRyeSgpDQoNCmBgYA0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQpib3hwbG90KGRhdGFfYWxsX2JveHBsb3QsIG1haW4gPSAiRG9ubsOpZXMgSERGIDEwIG1pbiDDoCBwaWVkIiwNCiAgICAgICAgbGFzID0gMikgIyBSb3RhdGUgbGFiZWxzIGJ5IDkwIGRlZ3JlZXMNCmBgYA0KDQo8YnI+DQo8YnI+DQo8YnI+DQoNCioqRGlzdHJpYnV0aW9uIGRlIGxhIHZhcmlhYmxlIGTDqXBlbmRhbnRlKioNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQpoaXN0KGFsbF9kYXRhJHZveV8yMDIyLA0KICAgICBmcmVxPVQsDQogICAgIGJyZWFrcyA9IDEwMCwNCiAgICAgY29sID0gImRhcmtibHVlIiwNCiAgICAgYm9yZGVyID0gIndoaXRlIiwNCiAgICAgbWFpbiA9ICJWb3lhZ2V1cnMgMjAyMiBIYXV0cy1kZS1GcmFuY2UiKQ0KYGBgDQoNCioqRMOpdGVjdGlvbiBkZXMgb3V0bGllcnMgYXZlYyBEQlNjYW4qKg0KDQoNCmxpYnJhcnkoZGJzY2FuKQ0KZGJzY2FuX3Jlc3VsdCA8LSBkYnNjYW4oYWxsX2RhdGEsIGVwcyA9IDUsIG1pblB0cyA9IDgpDQpkYnNjYW5fcmVzdWx0DQoNCg0KDQoqKlN1cHByZXNzaW9uIGRlcyB2YWxldXJzIGFiZXJyYW50ZXM6IGdhcmVzID49IMOgIDEwIHZveWFnZXVycyBwYXIgYW4gZXQgaW5mIMOgIDEwIDAwMCAwMDAqKg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQphbGxfZGF0YV9maWx0ZXIgPC0gYWxsX2RhdGEgJT4lDQogIGRwbHlyOjpmaWx0ZXIodm95XzIwMjIgPj0gMTAgJiB2b3lfMjAyMiA8IDEwMDAwMDAwKQ0KYGBgDQoNCg0KKipBcHBsaXF1ZXIgdW5lIHRyYW5zZm9ybWF0aW9uIGxvZ2FyaXRobWlxdWUgw6AgbGEgdmFyaWFibGUgZMOpcGVuZGFudGUqKg0KDQpUcmFuc2Zvcm1hdGlvbiBsb2dhcml0aG1pcXVlIDogRWxsZSBlc3QgcGFydGljdWxpw6hyZW1lbnQgdXRpbGUgcG91ciBsZXMgZG9ubsOpZXMgcXVpIHN1aXZlbnQgdW5lIGRpc3RyaWJ1dGlvbiBleHBvbmVudGllbGxlIG91IGxvZy1ub3JtYWxlLiBMYSB0cmFuc2Zvcm1hdGlvbiBwZXV0IGFpZGVyIMOgIHN0YWJpbGlzZXIgbGEgdmFyaWFuY2UgZGVzIHLDqXNpZHVzIGV0IMOgIHJlbmRyZSBsZXMgcmVsYXRpb25zIGVudHJlIGxlcyB2YXJpYWJsZXMgcGx1cyBsaW7DqWFpcmVzLCBjZSBxdWkgZXN0IHNvdWhhaXRhYmxlIGRhbnMgbGEgcsOpZ3Jlc3Npb24gbGluw6lhaXJlLg0KDQpgYGB7cn0NCmFsbF9kYXRhX2ZpbHRlciRsb2dfdm95XzIwMjIgPC0gbG9nKGFsbF9kYXRhX2ZpbHRlciR2b3lfMjAyMikNCmBgYA0KDQoqKkRpc3RyaWJ1dGlvbiBkZSBsYSB2YXJpYWJsZSBkw6lwZW5kYW50ZSB0cmFuc2Zvcm3DqWUqKg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCmhpc3QoYWxsX2RhdGFfZmlsdGVyJGxvZ192b3lfMjAyMiwNCiAgICAgZnJlcT1ULA0KICAgICBicmVha3MgPSAxMDAsDQogICAgIGNvbCA9ICJkYXJrYmx1ZSIsDQogICAgIGJvcmRlciA9ICJ3aGl0ZSIsDQogICAgIG1haW4gPSAiVm95YWdldXJzIDIwMjIgSGF1dHMtZGUtRnJhbmNlIikNCmBgYA0KKipOb3JtYWxpdMOpIGRlIGxhIHZhcmlhYmxlIGTDqXBlbmRhbnRlKioNCg0KTGEgdmFyaWFibGUgZMOpcGVuZGFudGUgdm95XzIwMjAgc3VpdCBiaWVuIHVuZSBsb2kgbm9ybWFsZSAocF92YWx1ZSA+IDAuMDUpDQoNCmBgYHtyfQ0KIyBOb3JtYWxpdMOpIFRlc3QgZGUgU2hhcGlyby1XaWxrDQpzaGFwaXJvLnRlc3QoYWxsX2RhdGFfZmlsdGVyJGxvZ192b3lfMjAyMikNCg0KYGBgDQoNCioqTWF0cmljZSBkZSBjb3Jyw6lsYXRpb24qKg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCmRhdGFfZm9yX2NvciA8LQ0KICBhbGxfZGF0YV9maWx0ZXJbLCBjKA0KICAgICJsb2dfdm95XzIwMjIiLA0KICAgICJzdW1fcG9wdWxhdGlvbiIsDQogICAgInN1bV9wb3B1bGF0aW9uX2FjdGl2ZSIsDQogICAgInN1bV9saXRzIiwNCiAgICAibG9uZ3VldXJfcm91dGUiLA0KICAgICJuYl9pbnRlcnNlY3Rpb25zIiwNCiAgICAjICJyZXNlYXVfcGVkZXN0cmUiICwNCiAgICAibG9uZ3VldXJfcGlzdGVzX2N5Y2xhYmxlcyIsDQogICAgIm5vbWJyZV9hcnJldHMiLA0KICAgICJub21icmVfcGFya2luZ3MiLA0KICAgICJub21icmVfY29tbWVyY2VzIiwNCiAgICAibm9tYnJlX3NhbnRlIiwNCiAgICAibm9tYnJlX2xvaXNpcnMiLA0KICAgICJub21icmVfcmVzdGF1cmF0aW9uIiwNCiAgICAibm9tYnJlX3Nwb3J0cyIsDQogICAgIm5vbWJyZV9yb25kc19wb2ludHMiLA0KICAgICJub21icmVfZWxldmVzIiwNCiAgICAiWkEiLA0KICAgICJwYXNzYWdlX25pdmVhdSIsDQogICAgInN1bV9wb3B1bGF0aW9uX2NhcnJlYXUiLA0KICAgICJQTlJfT0siDQogICldDQpkYXRhX2Zvcl9jb3IgPC0gc2Y6OnN0X2Ryb3BfZ2VvbWV0cnkoZGF0YV9mb3JfY29yKQ0KbWNvciA8LSBjb3IoZGF0YV9mb3JfY29yLCB1c2UgPSAiY29tcGxldGUub2JzIikNCg0KY29ycnBsb3Q6OmNvcnJwbG90KG1jb3IsDQogICAgICAgICAgICAgICAgICAgdHlwZT0idXBwZXIiLA0KICAgICAgICAgICAgICAgICAgIG9yZGVyPSJoY2x1c3QiLA0KICAgICAgICAgICAgICAgICAgIHRsLmNvbD0iYmxhY2siKQ0KYGBgDQoNCg0KIyMjIDIgLSBBbmFseXNlIGVuIGNvbXBvc2FudGVzIHByaW5jaXBhbGVzIChBQ1ApDQoNCkwnYW5hbHlzZSBlbiBjb21wb3NhbnRlcyBwcmluY2lwYWxlcyBjcsOpZSBkZSBub3V2ZWxsZXMgdmFyaWFibGVzIDogZGVzIGZhY3RldXJzIG91IGRlcyBjb21wb3NhbnRlcy4gTGVzIGZhY3RldXJzIHNvbnQgZGVzIGNvbWJpbmFpc29ucyBsaW7DqWFpcmVzIGRlcyB2YXJpYWJsZXMgaW50cm9kdWl0ZXMuIE9uIGNoZXJjaGUgw6AgcsOpZHVpcmUgbGUgbm9tYnJlIGRlIHZhcmlhYmxlcyBlbiBuZSBjb25zZXJ2YW50IHF1J3VuZSBvdSBkZXV4IHZhcmlhYmxlcyAoY29tcG9zYW50ZXMpIHJlZ3JvdXBhbnQgbGEgdmFyaWF0aW9uIGxhIHBsdXMgaW1wb3J0YW50ZSBkZSBsJ2Vuc2VtYmxlIGRlcyB2YXJpYWJsZXMgaW50cm9kdWl0ZXMuICAgDQpMZXMgdmFyaWFibGVzIGRlIGNoYXF1ZSAgY29tcG9zYW50ZSBzb250IGZvcnRlbWVudCBjb3Jyw6lsw6llcy4gIA0KRW4gbmUgY29uc2VydmFudCBxdWUgbGVzIHZhcmlhYmxlcyBsZXMgcGx1cyBpbXBvcnRhbnRlcyBkZSBjaGFxdWUgY29tcG9zYW50ZSwgb24gbmUgcGVyZCBwYXMgZCdpbmZvcm1hdGlvbiBtYWlzIG9uIHLDqWR1aXQgbGUgbm9tYnJlIGRlIHZhcmlhYmxlcy4gICANCg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCmdsaW1wc2UoYWxsX2RhdGFfZmlsdGVyKQ0KYGBgDQoNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQpkYXRhX3NlbGVjdCA8LSBhbGxfZGF0YV9maWx0ZXIgJT4lDQogIHNlbGVjdChzdW1fcG9wdWxhdGlvbiwNCiAgc3VtX3BvcHVsYXRpb25fYWN0aXZlLA0KICBzdW1fbGl0cywNCiAgbG9uZ3VldXJfcm91dGUsDQogIG5iX2ludGVyc2VjdGlvbnMsDQogICMgcmVzZWF1X3BlZGVzdHJlLA0KICBsb25ndWV1cl9waXN0ZXNfY3ljbGFibGVzLA0KICBub21icmVfYXJyZXRzLA0KICBub21icmVfcGFya2luZ3MsDQogIG5vbWJyZV9jb21tZXJjZXMsDQogIG5vbWJyZV9zYW50ZSwNCiAgbm9tYnJlX2xvaXNpcnMsDQogIG5vbWJyZV9yZXN0YXVyYXRpb24sDQogIG5vbWJyZV9zcG9ydHMsDQogIG5vbWJyZV9yb25kc19wb2ludHMsDQogIG5vbWJyZV9lbGV2ZXMsDQogIFpBLA0KICBwYXNzYWdlX25pdmVhdSwNCiAgc3VtX3BvcHVsYXRpb25fY2FycmVhdSwNCiAgUE5SX09LDQogICkgJT4lDQogIHNmOjpzdF9kcm9wX2dlb21ldHJ5KCkNCmBgYA0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJywgZXZhbCA9IEZ9DQojIENvZWZmaWNpZW50IGRlIGNvcnLDqWxhdGlvbiBkZSBQRUFSU09ODQojIENlcyBjb2VmZmljaWVudHMgbWVzdXJlbnQgbGEgZm9yY2UgZXQgbGEgZGlyZWN0aW9uIGRlIGxhIHJlbGF0aW9uIGxpbsOpYWlyZSBlbnRyZSBjaGFxdWUgcGFpcmUgZGUgdmFyaWFibGVzDQpzdGF0czo6Y29yKGRhdGFfc2VsZWN0LCB1c2UgPSAiY29tcGxldGUub2JzIikNCmBgYA0KDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnLCBlY2hvID0gVCwgZmlnLnNob3c9ImhpZGUifQ0KIyBMYW5jZW1lbnQgZGUgbCdBQ1ANClBDQSA8LSBGYWN0b01pbmVSOjpQQ0EoZGF0YV9zZWxlY3QsIA0KICAgICAgICAgICAgICAgICAgICAgICBxdWFudGkuc3VwID0gYygpLCANCiAgICAgICAgICAgICAgICAgICAgICAgcXVhbGkuc3VwID0gYygiUE5SX09LIiksICMgdmFsZXVyIGJpbmFpcmUgdHJhaXTDqWUgY29tbWUgdW5lIHZhcmlhYmxlIHN1cHBsw6ltZW50YWlyZQ0KICAgICAgICAgICAgICAgICAgICAgICBzY2FsZS51bml0ID0gVCkgIyBub3JtYWxpc2F0aW9uIGRlcyB2YXJpYWJsZXMNCmBgYA0KDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBwb2lkcyBkZSBjaGFxdWUgY29tcG9zYW50ZQ0KZmFjdG9leHRyYTo6ZnZpel9laWcoUENBLCBhZGRsYWJlbHMgPSBUUlVFLCB5bGltID0gYygwLCA1MCkpDQoNCiMgQ2VyY2xlIGRlcyBjb3Jyw6lsYXRpb25zDQpmYWN0b2V4dHJhOjpmdml6X3BjYV92YXIoUENBLCBjb2wudmFyPSJjb250cmliIiwNCiAgICAgICAgICAgICBncmFkaWVudC5jb2xzID0gYygiIzAwQUZCQiIsICIjRTdCODAwIiwgIiNGQzRFMDciKSwNCiAgICAgICAgICAgICByZXBlbCA9IFRSVUUpDQoNCiMgR3JhcGhpcXVlIGRlcyBpbmRpdmlkdXMNCmZhY3RvZXh0cmE6OmZ2aXpfcGNhX2luZChQQ0EsIGNvbC5pbmQgPSAiY29zMiIsDQogICAgICAgICAgICAgZ3JhZGllbnQuY29scyA9IGMoIiMwMEFGQkIiLCAiI0U3QjgwMCIsICIjRkM0RTA3IiksDQogICAgICAgICAgICAgcmVwZWwgPSBUUlVFKQ0KDQojIFRhYmxlYXUgZGVzIHZhbGV1cnMgcHJvcHJlcw0KUENBJGVpZw0KDQojIENvbnRyaWJ1dGlvbiBkZSBjaGFxdWUgdmFyaWFibGUgYXV4IGRldXggcHJlbWllcnMgYXhlcw0KZmFjdG9leHRyYTo6ZnZpel9jb250cmliKFBDQSwgY2hvaWNlID0gInZhciIsIGF4ZXMgPSAxKSAjIGF4ZSAxDQpmYWN0b2V4dHJhOjpmdml6X2NvbnRyaWIoUENBLCBjaG9pY2UgPSAidmFyIiwgYXhlcyA9IDIpICMgYXhlIDINCmZhY3RvZXh0cmE6OmZ2aXpfY29udHJpYihQQ0EsIGNob2ljZSA9ICJ2YXIiLCBheGVzID0gMykgIyBheGUgMw0KYGBgDQoNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJScsIGV2YWwgPSBGfQ0KIyBDb250cmlidXRpb24gZGUgY2hhcXVlIGluZGl2aWR1IGF1eCBkZXV4IHByZW1pZXJzIGF4ZXMNCmZhY3RvZXh0cmE6OmZ2aXpfY29udHJpYihQQ0EsIGNob2ljZSA9ICJpbmQiLCBheGVzID0gMSkNCmZhY3RvZXh0cmE6OmZ2aXpfY29udHJpYihQQ0EsIGNob2ljZSA9ICJpbmQiLCBheGVzID0gMikNCmZhY3RvZXh0cmE6OmZ2aXpfY29udHJpYihQQ0EsIGNob2ljZSA9ICJpbmQiLCBheGVzID0gMykNCmBgYA0KDQojIyMgMyAtIENsYXNzaWZpY2F0aW9uIGFzY2VuZGFudGUgaGnDqXJhcmNoaXF1ZSBldCBjYXJ0b2dyYXBoaWUNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQojIENBSCBzdXIgbGVzIHNjb3JlcyBkZXMgaW5kaXZpZHVzIGRlIGwnQUNQIC0tLS0NCmhjIDwtIEhDUEMoUENBLCBuYi5jbHVzdCA9IDMsIGdyYXBoID0gRkFMU0UpDQoNCiMgVmlzdWFsaXNlciBsZXMgZGVuZHJvZ3JhbW1lcw0KZnZpel9kZW5kKGhjLCBjZXggPSAwLjUpDQoNCiMgVmlzdWFsaXNlciBsZXMgaW5kaXZpZHVzIGRhbnMgbGUgcGxhbiBmYWN0b3JpZWwgYXZlYyB1bmUgaW5kaWNhdGlvbiBkZSBsZXVyIGNsdXN0ZXINCmZ2aXpfY2x1c3RlcihoYywgZ2VvbSA9ICJwb2ludCIpDQoNCiMgRXh0cmFjdGlvbiBkZXMgY2x1c3RlcnMgYXR0cmlidcOpcyDDoCBjaGFxdWUgb2JzZXJ2YXRpb24NCmNsdXN0ZXJzIDwtIGhjJGRhdGEuY2x1c3QkY2x1c3QNCmxlbmd0aChjbHVzdGVycykNCg0KIyBBam91dGVyIGxlcyBhZmZlY3RhdGlvbnMgZGUgY2x1c3RlciBhdXggZG9ubsOpZXMgb3JpZ2luYWxlcw0KbnJvdyhhbGxfZGF0YV9maWx0ZXIpDQphbGxfZGF0YV9maWx0ZXIkY2x1c3RlciA8LSBjbHVzdGVycw0KDQojIENhcnRvZ3JhcGhpZXIgbGVzIGNsdXN0ZXJzDQp0bWFwX21vZGUoJ3ZpZXcnKQ0KdG1fc2hhcGUoYWxsX2RhdGFfZmlsdGVyKSArDQogIHRtX2RvdHMoY29sID0gImNsdXN0ZXIiLCBwYWxldHRlID0gIlNldDEiLCB0aXRsZSA9ICJDbHVzdGVyIikgKw0KICB0bV9iYXNlbWFwKHNlcnZlciA9ICJPcGVuU3RyZWV0TWFwIikgKw0KICB0bV9sYXlvdXQobGVnZW5kLnBvc2l0aW9uID0gYygibGVmdCIsICJib3R0b20iKSkNCmBgYA0KDQoNCiMjIyA0IC0gQ29uc3RydWN0aW9uIGR1IG1vZMOobGUgZGUgcsOpZ3Jlc3Npb24gbGluw6lhaXJlDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KbW9kZWxlIDwtIGxtKA0KICBsb2dfdm95XzIwMjIgfg0KICBzdW1fcG9wdWxhdGlvbisNCiAgc3VtX3BvcHVsYXRpb25fYWN0aXZlKw0KICBzdW1fbGl0cysNCiAgbG9uZ3VldXJfcm91dGUrDQogIG5iX2ludGVyc2VjdGlvbnMrDQogICMgcmVzZWF1X3BlZGVzdHJlKw0KICBsb25ndWV1cl9waXN0ZXNfY3ljbGFibGVzKw0KICBub21icmVfYXJyZXRzKw0KICBub21icmVfcGFya2luZ3MrDQogIG5vbWJyZV9jb21tZXJjZXMrDQogIG5vbWJyZV9zYW50ZSsNCiAgbm9tYnJlX2xvaXNpcnMrDQogIG5vbWJyZV9yZXN0YXVyYXRpb24rDQogIG5vbWJyZV9zcG9ydHMrDQogIG5vbWJyZV9yb25kc19wb2ludHMrDQogIG5vbWJyZV9lbGV2ZXMrDQogIFpBKw0KICBwYXNzYWdlX25pdmVhdSsNCiAgc3VtX3BvcHVsYXRpb25fY2FycmVhdSsNCiAgUE5SX09LLA0KICBkYXRhID0gYWxsX2RhdGFfZmlsdGVyDQopDQoNCiMgQWZmaWNoYWdlIGR1IHLDqXN1bcOpIGR1IG1vZMOobGUgcG91ciB2b2lyIGxlcyBjb2VmZmljaWVudHMgZXQgbGEgc2lnbmlmaWNhdGl2aXTDqSBkZXMgdmFyaWFibGVzDQpzdW1tYXJ5KG1vZGVsZSkNCmBgYA0KDQoNCioqQ29lZmZpY2llbnQgZGUgZMOpdGVybWluYXRpb24qKg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCnN1bW1hcnlfbW9kZWxlIDwtIHN1bW1hcnkobW9kZWxlKQ0Kc3VtbWFyeV9tb2RlbGUkci5zcXVhcmVkDQpgYGANCg0KKipEaWFnbm9zdGljIHZpc3VlbCBkZXMgcsOpc2lkdXMqKg0KDQpRdWF0cmUgZ3JhcGhpcXVlcyBkZSBkaWFnbm9zdGljIHLDqXNpZHVlbHMgcG91ciBhaWRlciDDoCDDqXZhbHVlciBsYSBxdWFsaXTDqSBkZSBsJ2FqdXN0ZW1lbnQgZHUgbW9kw6hsZS4gQ2VzIGdyYXBoaXF1ZXMgZm91cm5pc3NlbnQgZGVzIGluZm9ybWF0aW9ucyB2aXN1ZWxsZXMgc3VyIGRpdmVycyBhc3BlY3RzIGRlcyByw6lzaWR1cyBldCBkZXMgYWp1c3RlbWVudHMgZHUgbW9kw6hsZSA6DQoNCiogKipPYnNlcnZhdGlvbiBkZXMgbGluw6lhcml0w6lzIGRlcyByZWxhdGlvbnMqKiA6IFLDqXNpZHVzIHZzIFZhbGV1cnMgUHLDqWRpdGVzIDogQ2UgZ3JhcGhpcXVlIG1vbnRyZSBsZXMgcsOpc2lkdXMgKGRpZmbDqXJlbmNlcyBlbnRyZSBsZXMgdmFsZXVycyBvYnNlcnbDqWVzIGV0IGxlcyB2YWxldXJzIHByw6lkaXRlcykgZW4gZm9uY3Rpb24gZGVzIHZhbGV1cnMgcHLDqWRpdGVzIHBhciBsZSBtb2TDqGxlLiBMJ2lkw6lhbCBlc3QgZGUgdm9pciB1bmUgZGlzcGVyc2lvbiBhbMOpYXRvaXJlIGRlcyBwb2ludHMgYXV0b3VyIGRlIGxhIGxpZ25lIGhvcml6b250YWxlIMOgIHrDqXJvLCBpbmRpcXVhbnQgbCdob21vc2PDqWRhc3RpY2l0w6kgKHZhcmlhbmNlIGNvbnN0YW50ZSBkZXMgcsOpc2lkdXMpLiBEZXMgbW90aWZzIG91IGRlcyB0ZW5kYW5jZXMgZGFucyBjZSBncmFwaGlxdWUgcGV1dmVudCBpbmRpcXVlciBkZXMgcHJvYmzDqG1lcyBkJ2jDqXTDqXJvc2PDqWRhc3RpY2l0w6kgb3UgZGVzICoqbm9uLWxpbsOpYXJpdMOpcyoqIG5vbiBjYXB0dXLDqWVzIHBhciBsZSBtb2TDqGxlLg0KDQoqICoqTm9ybWFsaXTDqSBkZXMgcsOpc2lkdXMqKiA6IFEtUSBQbG90IGRlcyBSw6lzaWR1cyBTdGFuZGFyZGlzw6lzIDogQ2UgZ3JhcGhpcXVlIGNvbXBhcmUgbGEgZGlzdHJpYnV0aW9uIGRlcyByw6lzaWR1cyBzdGFuZGFyZGlzw6lzIMOgIHVuZSBkaXN0cmlidXRpb24gbm9ybWFsZSB0aMOpb3JpcXVlLiBTaSBsZXMgcsOpc2lkdXMgc29udCBub3JtYWxlbWVudCBkaXN0cmlidcOpcywgbGVzIHBvaW50cyBkZXZyYWllbnQgYXBwcm94aW1hdGl2ZW1lbnQgc3VpdnJlIGxhIGxpZ25lIGRpYWdvbmFsZS4gRGVzIMOpY2FydHMgc2lnbmlmaWNhdGlmcyBkZSBjZXR0ZSBsaWduZSBwZXV2ZW50IGluZGlxdWVyIHVuZSB2aW9sYXRpb24gZGUgbCdoeXBvdGjDqHNlIGRlIG5vcm1hbGl0w6kgZGVzIHLDqXNpZHVzLCBjZSBxdWkgcGV1dCBhZmZlY3RlciBsZXMgdGVzdHMgZCdoeXBvdGjDqHNlIGV0IGxlcyBpbnRlcnZhbGxlcyBkZSBjb25maWFuY2UgYXNzb2Npw6lzIGF1IG1vZMOobGUuIChWb2lyIGF1c3NpIHRlc3QgZGUgU2hhcGlyby1XaWxrKQ0KDQoqICoqSG9tb3Njw6lkYXN0aWNpdMOpKiogU2NhbGUtTG9jYXRpb24gKG91IFNwcmVhZC1Mb2NhdGlvbikgOiBDZSBncmFwaGlxdWUgbW9udHJlIGxhIHJhY2luZSBjYXJyw6llIGRlcyB2YWxldXJzIGFic29sdWVzIGRlcyByw6lzaWR1cyBzdGFuZGFyZGlzw6lzIGVuIGZvbmN0aW9uIGRlcyB2YWxldXJzIHByw6lkaXRlcy4gSWwgZXN0IHV0aWxpc8OpIHBvdXIgdsOpcmlmaWVyIGwnaG9tb3Njw6lkYXN0aWNpdMOpIGRlcyByw6lzaWR1cy4gQ29tbWUgcG91ciBsZSBwcmVtaWVyIGdyYXBoaXF1ZSwgdW5lIGRpc3BlcnNpb24gYWzDqWF0b2lyZSBzYW5zIG1vdGlmIGNsYWlyIGVzdCBsJ2luZGljYXRldXIgZCd1bmUgYm9ubmUgaG9tb3Njw6lkYXN0aWNpdMOpLiBEZXMgbW90aWZzIG91IGRlcyB0ZW5kYW5jZXMgcGV1dmVudCBpbmRpcXVlciBkZXMgcHJvYmzDqG1lcyBkJ2jDqXTDqXJvc2PDqWRhc3RpY2l0w6kuIChWb2lyIGF1c3NpIHRlc3QgZGUgQnJldXNjaC1QYWdhbikNCg0KNC4gKipSw6lzaWR1cyB2cyBMZXZpZXJzIChvdSBMZXZlcmFnZSkqKiA6IENlIGdyYXBoaXF1ZSBtb250cmUgbGVzIHLDqXNpZHVzIHN0YW5kYXJkaXPDqXMgZW4gZm9uY3Rpb24gZGVzIGxldmllcnMgKG91IHZhbGV1cnMgZGUgbGV2aWVyKSBwb3VyIGNoYXF1ZSBvYnNlcnZhdGlvbi4gTGVzIHBvaW50cyBhdmVjIHVuIGxldmllciDDqWxldsOpIG9udCB1bmUgaW5mbHVlbmNlIHBsdXMgaW1wb3J0YW50ZSBzdXIgbCdhanVzdGVtZW50IGR1IG1vZMOobGUuIExlcyBvYnNlcnZhdGlvbnMgc2l0dcOpZXMgbG9pbiBkZSBsYSBtYWpvcml0w6kgZGVzIGRvbm7DqWVzIChlbiB0ZXJtZXMgZGUgdmFsZXVycyBkZSBsZXZpZXIpIG91IGF5YW50IGRlcyByw6lzaWR1cyBzdGFuZGFyZGlzw6lzIGltcG9ydGFudHMgc29udCBwYXJ0aWN1bGnDqHJlbWVudCBpbnTDqXJlc3NhbnRlcyBjYXIgZWxsZXMgcGV1dmVudCDDqnRyZSBkZXMgdmFsZXVycyBhYmVycmFudGVzIG91IGRlcyBwb2ludHMgaW5mbHVlbnRzLg0KDQo8YnI+DQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KcGxvdChtb2RlbGUpDQpgYGANCg0KDQoNCioqTm9ybWFsaXTDqSBkZXMgcsOpc2lkdXMqKg0KDQpMYSB2YWxldXIgcCBlc3QgZGUgMy44NTVlLTA4LCBjZSBxdWkgZXN0IGluZsOpcmlldXIgYXUgc2V1aWwgY29tbXVuIGRlIDAuMDUuIENlbGEgaW5kaXF1ZSBxdWUgbm91cyBhdm9ucyBzdWZmaXNhbW1lbnQgZGUgcHJldXZlcyBwb3VyIHJlamV0ZXIgbCdoeXBvdGjDqHNlIG51bGxlIGRlIG5vcm1hbGl0w6kgZGVzIHLDqXNpZHVzLiBFbiBkJ2F1dHJlcyB0ZXJtZXMsIGlsIHkgYSBkZXMgcHJldXZlcyBzdGF0aXN0aXF1ZXMgc3VnZ8OpcmFudCBxdWUgbGVzIHLDqXNpZHVzIGR1IG1vZMOobGUgbmUgc3VpdmVudCBwYXMgdW5lIGRpc3RyaWJ1dGlvbiBub3JtYWxlLg0KDQpgYGB7cn0NCiMgVGVzdCBkZSBTaGFwaXJvLVdpbGsNCnNoYXBpcm8udGVzdChyZXNpZHVhbHMobW9kZWxlKSkNCmBgYA0KDQoqKkhvbW9zY8OpZGFzdGljaXTDqSBkZXMgcsOpc2lkdXMgKGhvbW9nw6luw6lpdMOpKSoqDQoNCkF2ZWMgdW5lIHZhbGV1ciBwIGRlIDAuMjk4OTksIGNlIHRlc3QgbmUgcmVqZXR0ZSBwYXMgbCdoeXBvdGjDqHNlIG51bGxlIGQnaG9tb3Njw6lkYXN0aWNpdMOpIGF1IHNldWlsIGRlIHNpZ25pZmljYXRpdml0w6kgY29tbXVuIGRlIDAuMDUuIENlbGEgc3VnZ8OocmUgcXVlIGxlcyBkb25uw6llcyBuZSBtb250cmVudCBwYXMgZGUgcHJldXZlcyBzdGF0aXN0aXF1ZW1lbnQgc2lnbmlmaWNhdGl2ZXMgZCdow6l0w6lyb3Njw6lkYXN0aWNpdMOpIHNlbG9uIGNlIHRlc3QsIGV0IHF1ZSBsJ2Fzc29tcHRpb24gZCdob21vc2PDqWRhc3RpY2l0w6kgKHZhcmlhbmNlIGNvbnN0YW50ZSBkZXMgcsOpc2lkdXMpIHBvdXIgbGUgbW9kw6hsZSBkZSByw6lncmVzc2lvbiBlc3QgcmFpc29ubmFibGVtZW50IHNhdGlzZmFpdGUuDQoNCg0KYGBge3J9DQojIFRlc3QgZGUgQnJldXNjaC1QYWdhbg0KY2FyOjpuY3ZUZXN0KG1vZGVsZSkNCmBgYA0KPGJyPg0KDQojIyMgNSAtIE11bHRpY29saW7DqWFyaXTDqQ0KDQpM4oCZdW4gZGVzIHBvaW50cyBsZXMgcGx1cyBpbXBvcnRhbnRzIGVuIHLDqWdyZXNzaW9uIG11bHRpcGxlIGVzdCBkZSByZXNwZWN0ZXIgbOKAmWluZMOpcGVuZGFuY2UgZW50cmUgbGVzIHZhcmlhYmxlcyBleG9nw6huZXMgKGFic2VuY2UgZGUgY29saW7DqWFyaXTDqSksIGxlIHJpc3F1ZSDDqXRhbnQgc2lub24gZGUgYmlhaXNlciBsZXMgZXN0aW1hdGlvbnMgZGVzIGVycmV1cnMgdHlwZXMgZGVzIGNvZWZmaWNpZW50cyBkZSByw6lncmVzc2lvbi4NCkxhIFZJRiAodmFyaWFuY2UgaW5mbGF0aW9uIGZhY3RvcikgZXN0IHVuZSBib25uZSBtw6l0aG9kZSBwb3VyIGTDqXRlY3RlciBjZXMgcHJvYmzDqG1lcyBkZSBjb2xpbsOpYXJpdMOpLg0KDQpMZSAiVmFyaWFuY2UgSW5mbGF0aW9uIEZhY3RvciIgKFZJRikgZXN0IGNhbGN1bMOpIHBvdXIgY2hhcXVlIHZhcmlhYmxlIGV4cGxpY2F0aXZlIGQndW4gbW9kw6hsZSBkZSByw6lncmVzc2lvbi4gUG91ciBjYWxjdWxlciBsZSBWSUYgZCd1bmUgdmFyaWFibGUsIG9uIHLDqWFsaXNlIHVuZSByw6lncmVzc2lvbiBkZSBjZXR0ZSB2YXJpYWJsZSBlbiBmb25jdGlvbiBkZSB0b3V0ZXMgbGVzIGF1dHJlcyB2YXJpYWJsZXMgZXhwbGljYXRpdmVzIGR1IG1vZMOobGUuIExlIFZJRiBlc3QgZW5zdWl0ZSBjYWxjdWzDqSBjb21tZSDDqXRhbnQgMSBkaXZpc8OpIHBhciAoMSAtIFLCsikgZGUgY2V0dGUgcsOpZ3Jlc3Npb24sIG/DuSBSwrIgZXN0IGxlIGNvZWZmaWNpZW50IGRlIGTDqXRlcm1pbmF0aW9uIGRlIGxhIHLDqWdyZXNzaW9uLiBBaW5zaSwgbGUgVklGIG1lc3VyZSBjb21iaWVuIGxhIHZhcmlhbmNlIGQndW4gZXN0aW1hdGV1ciBkZSByw6lncmVzc2lvbiBlc3QgZ29uZmzDqWUgw6AgY2F1c2UgZGUgbGEgbXVsdGljb2xsaW7DqWFyaXTDqS4NCkxhIGZvbmN0aW9uIHZpZigpIGR1IHBhY2thZ2UgKmNhciogcGVybWV0IGRlIGxhIGNhbGN1bGVyLg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJywgZXZhbCA9IEZ9DQojIEZvbmN0aW9uIHZpZigpDQpjYXI6OnZpZihtb2RlbGUpDQpgYGANCg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCiMgVmlmIGF2ZWMgZ3RzdW1tYXJ5DQpndHN1bW1hcnk6OnRibF9yZWdyZXNzaW9uKG1vZGVsZSkgJT4lDQogIGd0c3VtbWFyeTo6YWRkX3ZpZigpDQpgYGANCg0KKioqDQoNCkxlcyB2YWxldXJzIGR1IEZhY3RldXIgZCdJbmZsYXRpb24gZGUgbGEgVmFyaWFuY2UgKFZJRikgZm91cm5pc3NlbnQgdW5lIGluZGljYXRpb24gZGUgbGEgcHLDqXNlbmNlIGRlIG11bHRpY29saW7DqWFyaXTDqSBwYXJtaSBsZXMgdmFyaWFibGVzIGV4cGxpY2F0aXZlcyBkYW5zIHVuIG1vZMOobGUgZGUgcsOpZ3Jlc3Npb24gbGluw6lhaXJlLiBFbiByw6hnbGUgZ8OpbsOpcmFsZSwgdW4gVklGIHN1cMOpcmlldXIgw6AgNSBlc3Qgc291dmVudCBjb25zaWTDqXLDqSBjb21tZSBpbmRpcXVhbnQgdW5lIGZvcnRlIG11bHRpY29saW7DqWFyaXTDqSwgbsOpY2Vzc2l0YW50IHVuZSBhY3Rpb24gcG91ciByw6lkdWlyZSBjZXR0ZSBtdWx0aWNvbGxpbsOpYXJpdMOpIGRhbnMgbGUgbW9kw6hsZS4NCg0KDQpgYGB7ciwgZWNobyA9IEYsIGV2YWwgPSBGfQ0KVmFyaWFibGVzIGF2ZWMgdW4gVklGIMOpbGV2w6kgKHN1cMOpcmlldXIgw6AgNSkgOg0KKiBzdW1fcG9wdWxhdGlvbiA6IFZJRiA9IDU5Nw0KKiBzdW1fcG9wdWxhdGlvbl9hY3RpdmUgOiBWSUYgPSA3MDINCiogc3VtX2xpdHMgOiBWSUYgPSAxNA0KKiBsb25ndWV1cl9yb3V0ZSA6IFZJRiA9IDc5DQoqIG5iX2ludGVyc2VjdGlvbnMgOiBWSUYgPSA1MQ0KKiByZXNlYXVfcGVkZXN0cmUgOiBWSUYgPSAzMg0KKiBub21icmVfY29tbWVyY2VzIDogVklGID0gMzUNCiogbm9tYnJlX3NhbnRlIDogVklGID0gIDguNQ0KKiBub21icmVfbG9pc2lycyA6IFZJRiA9IDEyDQoqIG5vbWJyZV9yZXN0YXVyYXRpb24gOiBWSUYgPSA0NA0KYGBgDQoNCjxicj4NCg0KIyMjIDYgLSBDb25zdHJ1Y3Rpb24gZHUgbW9kw6hsZSBkZSByw6lncmVzc2lvbiBsaW7DqWFpcmUgYXZlYyBtb2lucyBkZSB2YXJpYWJsZSAoVklGIDwgNSkNCg0KTm91cyBhdm9ucyBwcm9jw6lkw6kgZGUgbWFuacOocmUgaXTDqXJhdGl2ZSBlbiBzdXBwcmltYW50IGRlcyB2YXJpYWJsZXMgYXUgZnVyIGV0IMOgIG1lc3VyZS4gRmluYWxlbWVudCBub3VzIGNvbnNlcnZvbnMgbGVzIHZhbGV1cnMgc3VpdmFudGVzIDoNCg0KKiBzdW1fbGl0cw0KKiBsb25ndWV1cl9yb3V0ZQ0KKiBsb25ndWV1cl9waXN0ZXNfY3ljbGFibGVzDQoqIG5vbWJyZV9hcnJldHMNCiogbm9tYnJlX3BhcmtpbmdzDQoqIG5vbWJyZV9jb21tZXJjZXMNCiogbm9tYnJlX3Nwb3J0cw0KKiBub21icmVfcm9uZHNfcG9pbnRzDQoqIG5vbWJyZV9lbGV2ZXMNCiogcGFzc2FnZV9uaXZlYXUNCiogc3VtX3BvcHVsYXRpb25fY2FycmVhdQ0KKiBQTlJfT0sNCiogcGVudGUgKHBvdXIgbGUgdsOpbG8pDQoNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQptb2RlbGUgPC0gbG0oDQogIGxvZ192b3lfMjAyMiB+DQogICAgIyBzdW1fcG9wdWxhdGlvbisNCiAgICAjIHN1bV9wb3B1bGF0aW9uX2FjdGl2ZSsNCiAgICBzdW1fbGl0cysNCiAgICBsb25ndWV1cl9yb3V0ZSsNCiAgICAjIG5iX2ludGVyc2VjdGlvbnMrDQogICAgIyByZXNlYXVfcGVkZXN0cmUrDQogICAgbG9uZ3VldXJfcGlzdGVzX2N5Y2xhYmxlcysNCiAgICBub21icmVfYXJyZXRzKw0KICAgIG5vbWJyZV9wYXJraW5ncysNCiAgICBub21icmVfY29tbWVyY2VzKw0KICAgICMgbm9tYnJlX3NhbnRlKw0KICAgICMgbm9tYnJlX2xvaXNpcnMrDQogICAgIyBub21icmVfcmVzdGF1cmF0aW9uKw0KICAgIG5vbWJyZV9zcG9ydHMrDQogICAgbm9tYnJlX3JvbmRzX3BvaW50cysNCiAgICBub21icmVfZWxldmVzKw0KICAgICMgWkErDQogICAgcGFzc2FnZV9uaXZlYXUrDQogICAgc3VtX3BvcHVsYXRpb25fY2FycmVhdSsNCiAgICBQTlJfT0ssDQogIGRhdGEgPSBhbGxfZGF0YV9maWx0ZXINCikNCmBgYA0KDQoqKkFmZmljaGFnZSBkdSByw6lzdW3DqSBkdSBtb2TDqGxlIHBvdXIgdm9pciBsZXMgY29lZmZpY2llbnRzIGV0IGxhIHNpZ25pZmljYXRpdml0w6kgZGVzIHZhcmlhYmxlcyoqDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCnN1bW1hcnkobW9kZWxlKQ0KYGBgDQoNClVuIG1vZMOobGUgZGUgcsOpZ3Jlc3Npb24gbGluw6lhaXJlIG11bHRpcGxlIHBlcm1ldCBkZSBmYWlyZSB0cm9pcyBjaG9zZXMgcHJpbmNpcGFsZXMgYXZlYyBsZXMgdmFyaWFibGVzIGQndW5lIMOpdHVkZSA6ICANCg0KKiBUcm91dmVyIGRlcyBDb2VmZmljaWVudHMgOiBsZSBtb2TDqGxlIGRvbm5lIHVuIGNvZWZmaWNpZW50ICh1biBub21icmUpIHBvdXIgY2hhcXVlIHZhcmlhYmxlIGluZMOpcGVuZGFudGUgZXhhbWluw6llLiBDZSBjb2VmZmljaWVudCBub3VzIGRpdCBjb21tZW50LCBldCBkZSBjb21iaWVuLCBvbiBwZXV0IHMnYXR0ZW5kcmUgw6AgY2UgcXVlIGxhIHZhcmlhYmxlIGTDqXBlbmRhbnRlIGNoYW5nZSBxdWFuZCBsYSB2YXJpYWJsZSBpbmTDqXBlbmRhbnRlIGNoYW5nZSBkJ3VuZSB1bml0w6ksIGVuIGdhcmRhbnQgdG91dGVzIGxlcyBhdXRyZXMgdmFyaWFibGVzIGNvbnN0YW50ZXMuICANCg0KKiBKdWdlciBkZSBsZXVyIEZvcmNlIDogTGEgdGFpbGxlIG91IGxhIHZhbGV1ciBhYnNvbHVlIGRlIGNoYXF1ZSBjb2VmZmljaWVudCBub3VzIGRvbm5lIHVuZSBpZMOpZSBkZSBsYSBmb3JjZSBkZSBsJ2VmZmV0IGRlIGNldHRlIHZhcmlhYmxlIGluZMOpcGVuZGFudGUgc3VyIGxhIHZhcmlhYmxlIGTDqXBlbmRhbnRlLiBVbiBncmFuZCBjb2VmZmljaWVudCAoZW4gdmFsZXVyIGFic29sdWUpIHNpZ25pZmllIHVuIGdyYW5kIGVmZmV0IDogc2kgbGEgdmFyaWFibGUgaW5kw6lwZW5kYW50ZSBhdWdtZW50ZSBkJ3VuIHBldSwgbGEgdmFyaWFibGUgZMOpcGVuZGFudGUgY2hhbmdlIGRlIGJlYXVjb3VwLiAgDQoNCiogw4l2YWx1ZXIgbGV1ciBTaWduaWZpY2F0aXZpdMOpIDogTGUgbW9kw6hsZSBub3VzIGRvbm5lIGF1c3NpIHVuZSB2YWxldXIgcCBwb3VyIGNoYXF1ZSBjb2VmZmljaWVudCwgcXVpIG5vdXMgZGl0IHNpIGwnZWZmZXQgb2JzZXJ2w6kgZXN0IHN0YXRpc3RpcXVlbWVudCBzaWduaWZpY2F0aWYuIFVuZSB2YWxldXIgcCBmYWlibGUgKHNvdXZlbnQgbW9pbnMgZGUgMCwwNSkgc3VnZ8OocmUgcXVlIGwnZWZmZXQgbidlc3QgcHJvYmFibGVtZW50IHBhcyBkw7sgYXUgaGFzYXJkLCBldCBxdWUgbGEgdmFyaWFibGUgaW5kw6lwZW5kYW50ZSBhIHZyYWltZW50IHVuIGltcGFjdCBzdXIgbGEgdmFyaWFibGUgZMOpcGVuZGFudGUuDQoNCkVuIHNvbW1lLCBsYSByw6lncmVzc2lvbiBsaW7DqWFpcmUgbXVsdGlwbGUgZXN0IHVuIG91dGlsIHV0aWxlIHBvdXIgY29tcHJlbmRyZSBldCBxdWFudGlmaWVyIGxlcyByZWxhdGlvbnMgZW50cmUgdW5lIHZhcmlhYmxlIGTDqXBlbmRhbnRlIGV0IHBsdXNpZXVycyB2YXJpYWJsZXMgaW5kw6lwZW5kYW50ZXMsIGVuIG5vdXMgcGVybWV0dGFudCBkZSB2b2lyIG5vbiBzZXVsZW1lbnQgcXVlbHMgZmFjdGV1cnMgc29udCBpbXBvcnRhbnRzLCBtYWlzIGF1c3NpIGNvbW1lbnQgaWxzIHNvbnQgaW1wb3J0YW50cy4NCg0KDQoqIHZhbGV1ciB0IGNvbW1lIMOgIHVuIHNjb3JlIGRlIGZvcmNlIG91IGRlIGNsYXJ0w6kgZGUgbCdvYnNlcnZhdGlvbiAgICANCiogdmFsZXVyIHAgY29tbWUgw6AgdW4gaW5kaWNhdGV1ciBkZSBsJ2ltcG9ydGFuY2Ugb3UgZGUgbGEgc2lnbmlmaWNhdGl2aXTDqSBkZWwnb2JzZXJ2YXRpb24gICAgDQoqIE5vcm1hbGVtZW50LCB1bmUgdmFsZXVyIHQgw6lsZXbDqWUgaW5kaXF1ZSB1bmUgZGlmZsOpcmVuY2UgbWFycXXDqWUgZW50cmUgbGUgZ3JvdXBlIG9ic2VydsOpIGV0IGxlIGdyb3VwZSBkZSByw6lmw6lyZW5jZSwgY2UgcXVpIGNvbmR1aXQgZ8OpbsOpcmFsZW1lbnQgw6AgdW5lIHZhbGV1ciBwIGZhaWJsZSwgc3VnZ8OpcmFudCBxdWUgbGVzIHLDqXN1bHRhdHMgc29udCBzdGF0aXN0aXF1ZW1lbnQgc2lnbmlmaWNhdGlmcy4gICANCg0KDQoqKkNvZWZmaWNpZW50IGRlIGTDqXRlcm1pbmF0aW9uKioNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQpzdW1tYXJ5X21vZGVsZSA8LSBzdW1tYXJ5KG1vZGVsZSkNCnN1bW1hcnlfbW9kZWxlJHIuc3F1YXJlZA0KDQojIERpYWdub3N0aWMgdmlzdWVsIGRlcyByw6lzaWR1cw0KcGxvdChtb2RlbGUpDQpgYGANCg0KDQoNCg0KDQpgYGB7cn0NCiMgTm9ybWFsaXTDqSBkZXMgcsOpc2lkdXMNCiMgVGVzdCBkZSBTaGFwaXJvLVdpbGsNCnNoYXBpcm8udGVzdChyZXNpZHVhbHMobW9kZWxlKSkNCmBgYA0KDQoNCmBgYHtyfQ0KIyBIb21vc2PDqWRhc3RpY2l0w6kgZGVzIHLDqXNpZHVzIChob21vZ8OpbsOpaXTDqSkNCiMgVGVzdCBkZSBCcmV1c2NoLVBhZ2FuDQpjYXI6Om5jdlRlc3QobW9kZWxlKQ0KYGBgDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnLCBldmFsID0gRn0NCmNhcjo6dmlmKG1vZGVsZSkNCmBgYA0KDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBBdmVjIGxlIHBhY2thZ2UgZ3RzdW1tYXJ5IDoNCmd0c3VtbWFyeTo6dGJsX3JlZ3Jlc3Npb24obW9kZWxlKSAlPiUNCiAgZ3RzdW1tYXJ5OjphZGRfdmlmKCklPiUNCiAgZ3RzdW1tYXJ5Ojphc19ndCgpICU+JQ0KICBndDo6dGFiX2Zvb3Rub3RlKA0KICAgIGZvb3Rub3RlID0gIkRvbm7DqWVzIEhhdXRzLWRlLUZyYW5jZSIpDQoNCiMgT3UgcHLDqXNlbnTDqSBkZSBmYcOnb24gZ3JhcGhpcXVlIGF2ZWMgbGUgcGFja2FnZSBHR2FsbHkgOg0KR0dhbGx5OjpnZ2NvZWZfbW9kZWwobW9kZWxlKQ0KYGBgDQoNCg0KYGBge3J9DQpsaWJyYXJ5KGdncGxvdDIpDQoNCmdncGxvdChkYXRhID0gYWxsX2RhdGFfZmlsdGVyLCBhZXMoeCA9IGxvbmd1ZXVyX3JvdXRlLCB5ID0gbG9nX3ZveV8yMDIyKSkgKw0KICBnZW9tX3BvaW50KCkgKw0KICB0aGVtZV9taW5pbWFsKCkgKw0KICBsYWJzKHggPSAibG9uZ3VldXJfcm91dGUiLCB5ID0gIk5vbWJyZSBkZSB2b3lhZ2V1cnMiLCB0aXRsZSA9ICJSZWxhdGlvbiBlbnRyZSBsYSBsb25ndWV1cl9yb3V0ZSBldCBsZSBub21icmUgZGUgdm95YWdldXJzIikNCg0KZ2dwbG90KGRhdGEgPSBhbGxfZGF0YV9maWx0ZXIsIGFlcyh4ID0gbm9tYnJlX2FycmV0cywgeSA9IGxvZ192b3lfMjAyMikpICsNCiAgZ2VvbV9wb2ludCgpICsNCiAgdGhlbWVfbWluaW1hbCgpICsNCiAgbGFicyh4ID0gIm5vbWJyZV9hcnJldHMiLCB5ID0gIk5vbWJyZSBkZSB2b3lhZ2V1cnMiLCB0aXRsZSA9ICJSZWxhdGlvbiBlbnRyZSBub21icmVfYXJyZXRzIGV0IGxlIG5vbWJyZSBkZSB2b3lhZ2V1cnMiKQ0KDQpnZ3Bsb3QoZGF0YSA9IGFsbF9kYXRhX2ZpbHRlciwgYWVzKHggPSBub21icmVfcGFya2luZ3MsIHkgPSBsb2dfdm95XzIwMjIpKSArDQogIGdlb21fcG9pbnQoKSArDQogIHRoZW1lX21pbmltYWwoKSArDQogIGxhYnMoeCA9ICJub21icmVfcGFya2luZ3MiLCB5ID0gIk5vbWJyZSBkZSB2b3lhZ2V1cnMiLCB0aXRsZSA9ICJSZWxhdGlvbiBlbnRyZSBub21icmVfcGFya2luZ3MgZXQgbGUgbm9tYnJlIGRlIHZveWFnZXVycyIpDQoNCmdncGxvdChkYXRhID0gYWxsX2RhdGFfZmlsdGVyLCBhZXMoeCA9IHN1bV9saXRzLCB5ID0gbG9nX3ZveV8yMDIyKSkgKw0KICBnZW9tX3BvaW50KCkgKw0KICB0aGVtZV9taW5pbWFsKCkgKw0KICBsYWJzKHggPSAic3VtX2xpdHMiLCB5ID0gIk5vbWJyZSBkZSB2b3lhZ2V1cnMiLCB0aXRsZSA9ICJSZWxhdGlvbiBlbnRyZSBsYSBzdW1fbGl0cyBldCBsZSBub21icmUgZGUgdm95YWdldXJzIikNCg0KZ2dwbG90KGRhdGEgPSBhbGxfZGF0YV9maWx0ZXIsIGFlcyh4ID0gcGFzc2FnZV9uaXZlYXUsIHkgPSBsb2dfdm95XzIwMjIpKSArDQogIGdlb21fcG9pbnQoKSArDQogIHRoZW1lX21pbmltYWwoKSArDQogIGxhYnMoeCA9ICJwYXNzYWdlX25pdmVhdSIsIHkgPSAiTm9tYnJlIGRlIHZveWFnZXVycyIsIHRpdGxlID0gIlJlbGF0aW9uIGVudHJlIHBhc3NhZ2Vfbml2ZWF1IGV0IGxlIG5vbWJyZSBkZSB2b3lhZ2V1cnMiKQ0KDQpgYGANCg0KDQojIyMgNyAtIEFuYWx5c2UgZW4gY29tcG9zYW50ZXMgcHJpbmNpcGFsZXMgKEFDUCkNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQpnbGltcHNlKGFsbF9kYXRhX2ZpbHRlcikNCmBgYA0KDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KZGF0YV9zZWxlY3QgPC0gYWxsX2RhdGFfZmlsdGVyICU+JQ0KICBzZWxlY3QoIyBzdW1fcG9wdWxhdGlvbisNCiAgICAjIHN1bV9wb3B1bGF0aW9uX2FjdGl2ZSsNCiAgICBzdW1fbGl0cywNCiAgICBsb25ndWV1cl9yb3V0ZSwNCiAgICAjIG5iX2ludGVyc2VjdGlvbnMrDQogICAgIyByZXNlYXVfcGVkZXN0cmUrDQogICAgbG9uZ3VldXJfcGlzdGVzX2N5Y2xhYmxlcywNCiAgICBub21icmVfYXJyZXRzLA0KICAgIG5vbWJyZV9wYXJraW5ncywNCiAgICBub21icmVfY29tbWVyY2VzLA0KICAgICMgbm9tYnJlX3NhbnRlKw0KICAgICMgbm9tYnJlX2xvaXNpcnMrDQogICAgIyBub21icmVfcmVzdGF1cmF0aW9uKw0KICAgIG5vbWJyZV9zcG9ydHMsDQogICAgbm9tYnJlX3JvbmRzX3BvaW50cywNCiAgICBub21icmVfZWxldmVzLA0KICAgICMgWkErDQogICAgcGFzc2FnZV9uaXZlYXUsDQogICAgc3VtX3BvcHVsYXRpb25fY2FycmVhdSwNCiAgICBQTlJfT0sNCiAgKSAlPiUNCiAgc2Y6OnN0X2Ryb3BfZ2VvbWV0cnkoKQ0KYGBgDQoNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJScsIGV2YWwgPSBGfQ0KIyBDb2VmZmljaWVudCBkZSBjb3Jyw6lsYXRpb24gZGUgUEVBUlNPTg0KIyBDZXMgY29lZmZpY2llbnRzIG1lc3VyZW50IGxhIGZvcmNlIGV0IGxhIGRpcmVjdGlvbiBkZSBsYSByZWxhdGlvbiBsaW7DqWFpcmUgZW50cmUgY2hhcXVlIHBhaXJlIGRlIHZhcmlhYmxlcw0Kc3RhdHM6OmNvcihkYXRhX3NlbGVjdCwgdXNlID0gImNvbXBsZXRlLm9icyIpDQpgYGANCg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJywgZWNobyA9IFQsIGZpZy5zaG93PSJoaWRlIn0NCiMgTGFuY2VtZW50IGRlIGwnQUNQDQpQQ0EgPC0gRmFjdG9NaW5lUjo6UENBKGRhdGFfc2VsZWN0LCANCiAgICAgICAgICAgICAgICAgICAgICAgcXVhbnRpLnN1cCA9IGMoKSwgDQogICAgICAgICAgICAgICAgICAgICAgIHF1YWxpLnN1cCA9IGMoIlBOUl9PSyIpLCAjIHZhbGV1ciBiaW5haXJlIHRyYWl0w6llIGNvbW1lIHVuZSB2YXJpYWJsZSBzdXBwbMOpbWVudGFpcmUNCiAgICAgICAgICAgICAgICAgICAgICAgc2NhbGUudW5pdCA9IFQpICMgbm9ybWFsaXNhdGlvbiBkZXMgdmFyaWFibGVzDQpgYGANCg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCiMgcG9pZHMgZGUgY2hhcXVlIGNvbXBvc2FudGUNCmZhY3RvZXh0cmE6OmZ2aXpfZWlnKFBDQSwgYWRkbGFiZWxzID0gVFJVRSwgeWxpbSA9IGMoMCwgNTApKQ0KDQojIENlcmNsZSBkZXMgY29ycsOpbGF0aW9ucw0KZmFjdG9leHRyYTo6ZnZpel9wY2FfdmFyKFBDQSwgY29sLnZhcj0iY29udHJpYiIsDQogICAgICAgICAgICAgZ3JhZGllbnQuY29scyA9IGMoIiMwMEFGQkIiLCAiI0U3QjgwMCIsICIjRkM0RTA3IiksDQogICAgICAgICAgICAgcmVwZWwgPSBUUlVFKQ0KDQojIEdyYXBoaXF1ZSBkZXMgaW5kaXZpZHVzDQpmYWN0b2V4dHJhOjpmdml6X3BjYV9pbmQoUENBLCBjb2wuaW5kID0gImNvczIiLA0KICAgICAgICAgICAgIGdyYWRpZW50LmNvbHMgPSBjKCIjMDBBRkJCIiwgIiNFN0I4MDAiLCAiI0ZDNEUwNyIpLA0KICAgICAgICAgICAgIHJlcGVsID0gVFJVRSkNCg0KIyBUYWJsZWF1IGRlcyB2YWxldXJzIHByb3ByZXMNClBDQSRlaWcNCg0KIyBDb250cmlidXRpb24gZGUgY2hhcXVlIHZhcmlhYmxlIGF1eCBkZXV4IHByZW1pZXJzIGF4ZXMNCmZhY3RvZXh0cmE6OmZ2aXpfY29udHJpYihQQ0EsIGNob2ljZSA9ICJ2YXIiLCBheGVzID0gMSkgIyBheGUgMQ0KZmFjdG9leHRyYTo6ZnZpel9jb250cmliKFBDQSwgY2hvaWNlID0gInZhciIsIGF4ZXMgPSAyKSAjIGF4ZSAyDQpmYWN0b2V4dHJhOjpmdml6X2NvbnRyaWIoUENBLCBjaG9pY2UgPSAidmFyIiwgYXhlcyA9IDMpICMgYXhlIDMNCmBgYA0KDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnLCBldmFsID0gRn0NCiMgQ29udHJpYnV0aW9uIGRlIGNoYXF1ZSBpbmRpdmlkdSBhdXggZGV1eCBwcmVtaWVycyBheGVzDQpmYWN0b2V4dHJhOjpmdml6X2NvbnRyaWIoUENBLCBjaG9pY2UgPSAiaW5kIiwgYXhlcyA9IDEpDQpmYWN0b2V4dHJhOjpmdml6X2NvbnRyaWIoUENBLCBjaG9pY2UgPSAiaW5kIiwgYXhlcyA9IDIpDQpmYWN0b2V4dHJhOjpmdml6X2NvbnRyaWIoUENBLCBjaG9pY2UgPSAiaW5kIiwgYXhlcyA9IDMpDQpgYGANCg0KIyMjIDggLSBDbGFzc2lmaWNhdGlvbiBhc2NlbmRhbnRlIGhpw6lyYXJjaGlxdWUgZXQgY2FydG9ncmFwaGllDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBDQUggc3VyIGxlcyBzY29yZXMgZGVzIGluZGl2aWR1cyBkZSBsJ0FDUCAtLS0tDQpoYyA8LSBIQ1BDKFBDQSwgbmIuY2x1c3QgPSAzLCBncmFwaCA9IEZBTFNFKQ0KDQojIFZpc3VhbGlzZXIgbGVzIGRlbmRyb2dyYW1tZXMNCmZ2aXpfZGVuZChoYywgY2V4ID0gMC41KQ0KDQojIFZpc3VhbGlzZXIgbGVzIGluZGl2aWR1cyBkYW5zIGxlIHBsYW4gZmFjdG9yaWVsIGF2ZWMgdW5lIGluZGljYXRpb24gZGUgbGV1ciBjbHVzdGVyDQpmdml6X2NsdXN0ZXIoaGMsIGdlb20gPSAicG9pbnQiKQ0KDQojIEV4dHJhY3Rpb24gZGVzIGNsdXN0ZXJzIGF0dHJpYnXDqXMgw6AgY2hhcXVlIG9ic2VydmF0aW9uDQpjbHVzdGVycyA8LSBoYyRkYXRhLmNsdXN0JGNsdXN0DQpsZW5ndGgoY2x1c3RlcnMpDQoNCiMgQXNzdXJlei12b3VzIHF1ZSB2b3MgZG9ubsOpZXMgb3JpZ2luYWxlcyBvbnQgdW4gaWRlbnRpZmlhbnQgdW5pcXVlIHBvdXIgY2hhcXVlIG9ic2VydmF0aW9uDQojIEFqb3V0ZXIgbGVzIGFmZmVjdGF0aW9ucyBkZSBjbHVzdGVyIMOgIHZvcyBkb25uw6llcyBvcmlnaW5hbGVzDQpucm93KGFsbF9kYXRhX2ZpbHRlcikNCmFsbF9kYXRhX2ZpbHRlciRjbHVzdGVyIDwtIGNsdXN0ZXJzDQoNCg0KIyBDYXJ0b2dyYXBoaWVyIGxlcyBjbHVzdGVycw0KdG1hcF9tb2RlKCd2aWV3JykNCg0KdG1fYmFzZW1hcChjKGxlYWZsZXQ6OnByb3ZpZGVycyRFc3JpLldvcmxkVG9wb01hcCwNCiAgICAgICAgICAgICBsZWFmbGV0Ojpwcm92aWRlcnMkT3BlblN0cmVldE1hcCwNCiAgICAgICAgICAgICBsZWFmbGV0Ojpwcm92aWRlcnMkRXNyaS5Xb3JsZEltYWdlcnlpZGVycywNCiAgICAgICAgICAgICBsZWFmbGV0Ojpwcm92aWRlcnMkR2VvcG9ydGFpbEZyYW5jZS5vcnRob3MpKSArDQoNCnRtX3NoYXBlKGFsbF9kYXRhX2ZpbHRlcikgKw0KICB0bV9kb3RzKGNvbCA9ICJjbHVzdGVyIiwgcGFsZXR0ZSA9ICJTZXQxIiwgdGl0bGUgPSAiQ2x1c3RlciIpICsNCiAgdG1fYmFzZW1hcChzZXJ2ZXIgPSAiT3BlblN0cmVldE1hcCIpICsNCiAgdG1fbGF5b3V0KGxlZ2VuZC5wb3NpdGlvbiA9IGMoImxlZnQiLCAiYm90dG9tIikpDQpgYGANCg0KDQojIyMgOSAtIEJPWFBMT1RTDQoNCg0KYGBge3J9DQpkb25uZWVzX2xvbmd1ZXMgPC0gdGlkeXI6OnBpdm90X2xvbmdlcihhbGxfZGF0YV9maWx0ZXIsDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGNvbHMgPSBjKA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAjIHN1bV9wb3B1bGF0aW9uLA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICMgc3VtX3BvcHVsYXRpb25fYWN0aXZlLA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIHN1bV9saXRzLA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGxvbmd1ZXVyX3JvdXRlLA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICMgbmJfaW50ZXJzZWN0aW9ucywNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAjIHJlc2VhdV9wZWRlc3RyZSwNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBsb25ndWV1cl9waXN0ZXNfY3ljbGFibGVzLA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIG5vbWJyZV9hcnJldHMsDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgbm9tYnJlX3BhcmtpbmdzLA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIG5vbWJyZV9jb21tZXJjZXMsDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIyBub21icmVfc2FudGUsDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIyBub21icmVfbG9pc2lycywNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAjIG5vbWJyZV9yZXN0YXVyYXRpb24sDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgbm9tYnJlX3Nwb3J0cywNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBub21icmVfcm9uZHNfcG9pbnRzLA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIG5vbWJyZV9lbGV2ZXMsDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIyBaQSwNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBwYXNzYWdlX25pdmVhdSwNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBzdW1fcG9wdWxhdGlvbl9jYXJyZWF1LA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIFBOUl9PSyksDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIG5hbWVzX3RvID0gIlZhcmlhYmxlIiwNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgdmFsdWVzX3RvID0gIlZhbGV1ciIpDQoNCmBgYA0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCmdncGxvdChkb25uZWVzX2xvbmd1ZXMsIGFlcyh4ID0gYXMuZmFjdG9yKGNsdXN0ZXIpLCB5ID0gVmFsZXVyLCBmaWxsID0gYXMuZmFjdG9yKGNsdXN0ZXIpKSkgKw0KICBnZW9tX2JveHBsb3QoKSArDQogIGZhY2V0X3dyYXAofiBWYXJpYWJsZSwgc2NhbGVzID0gImZyZWVfeSIpICsgIyBDcsOpZSB1biBwYW5lbCBwb3VyIGNoYXF1ZSB2YXJpYWJsZQ0KICBsYWJzKHggPSAiQ2x1c3RlciIsIHkgPSAiVmFsZXVyIikgKw0KICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIlBhc3RlbDEiKSArICMgVXRpbGlzZXIgdW5lIHBhbGV0dGUgZGUgY291bGV1cnMNCiAgdGhlbWVfbWluaW1hbCgpICsNCiAgdGhlbWUobGVnZW5kLnRpdGxlID0gZWxlbWVudF9ibGFuaygpLCBheGlzLnRleHQueCA9IGVsZW1lbnRfdGV4dChhbmdsZSA9IDQ1LCBoanVzdCA9IDEpKSAjIFBlcnNvbm5hbGlzZSBsZSBncmFwaGlxdWUNCg0KYGBgDQoNCg0KIyMgQ09SUkVMQVRJT04NCg0KIyMjIENvcnLDqWxhdGlvbiBlbnRyZSBsZXMgdmFyaWFibGVzIGTDqXBlbmRhbnRlcw0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCiMgUGFja2FnZXMNCnBhY21hbjo6cF9sb2FkKGRwbHlyLCBzZiwgdGlkeXIsIGd0LCBnZ3Bsb3QyKQ0KYGBgDQoNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQojIENoYXJnZW1lbnQgZGVzIGRvbm7DqWVzDQphbGxfZGF0YTwtIHNmOjpzdF9yZWFkKCdwcm9jZXNzZWRfZGF0YS9hbGxfZGF0YV9zdGFuZGFyZGl6ZWRfc3Rwb2xfZm9vdF8xMG1pbl9wb3BfY2FycmVhdV8yMDI0MDMwNy5ncGtnJykNCmBgYA0KDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KbmFtZXMoYWxsX2RhdGEpDQpkYXRhX3NlbGVjdCA8LSBhbGxfZGF0YSAlPiUgDQogIHNlbGVjdChzdW1fcG9wdWxhdGlvbiwNCiAgICAgICAgIHN1bV9wb3B1bGF0aW9uX2NhcnJlYXUsDQogICAgICAgICBzdW1fcG9wdWxhdGlvbl9hY3RpdmUsDQogICAgICAgICBzdW1fbGl0cywNCiAgICAgICAgIGxvbmd1ZXVyX3JvdXRlLA0KICAgICAgICAgbmJfaW50ZXJzZWN0aW9ucywNCiAgICAgICAgIHJlc2VhdV9wZWRlc3RyZSwNCiAgICAgICAgIGxvbmd1ZXVyX3Bpc3Rlc19jeWNsYWJsZXMsDQogICAgICAgICBub21icmVfYXJyZXRzLA0KICAgICAgICAgbm9tYnJlX3BhcmtpbmdzLA0KICAgICAgICAgbm9tYnJlX2NvbW1lcmNlcywNCiAgICAgICAgIG5vbWJyZV9zYW50ZSwNCiAgICAgICAgIG5vbWJyZV9sb2lzaXJzLA0KICAgICAgICAgbm9tYnJlX3Jlc3RhdXJhdGlvbiwNCiAgICAgICAgIG5vbWJyZV9zcG9ydHMsDQogICAgICAgICBub21icmVfcm9uZHNfcG9pbnRzLA0KICAgICAgICAgbm9tYnJlX2VsZXZlcywNCiAgICAgICAgIFpBLA0KICAgICAgICAgcGFzc2FnZV9uaXZlYXUNCiAgICAgICAgICkgJT4lIA0KICBzdF9kcm9wX2dlb21ldHJ5KCkNCmBgYA0KDQoqKkNvZWZmaWNpZW50IGRlIGNvcnLDqWxhdGlvbioqDQoNCkNpLWRlc3NvdXMgYXZlYyBsYSBtw6l0aG9kZSBkZSBQZWFyc29uIChtw6l0aG9kZSBwYXIgZMOpZmF1dCkuIExhIGNvcnLDqWxhdGlvbiBkZSBQZWFyc29uIGVzdCBhcHByb3ByacOpZSBwb3VyIGRlcyBkb25uw6llcyBjb250aW51ZXMgZXQgbm9ybWFsZW1lbnQgZGlzdHJpYnXDqWVzLCBtZXN1cmFudCBsZXMgcmVsYXRpb25zIGxpbsOpYWlyZXMuICAgDQpFbGxlIG1lc3VyZSBsZSBkZWdyw6kgZGUgcmVsYXRpb24gbGluw6lhaXJlIGVudHJlIGRldXggdmFyaWFibGVzIHF1YW50aXRhdGl2ZXMuIEVuIGQnYXV0cmVzIHRlcm1lcywgZWxsZSBjaGVyY2hlIMOgIGTDqXRlcm1pbmVyIHNpLCBsb3JzcXVlIGwndW5lIGRlcyB2YXJpYWJsZXMgYXVnbWVudGUgb3UgZGltaW51ZSwgbCdhdXRyZSB2YXJpYWJsZSB0ZW5kIMOpZ2FsZW1lbnQgw6AgYXVnbWVudGVyIG91IGRpbWludWVyIHNlbG9uIHVuIG1vZMOobGUgcHLDqXZpc2libGUgZXQgY29uc3RhbnQsIGNlIHF1aSBzZXJhaXQgY2FyYWN0w6lyaXN0aXF1ZSBkJ3VuZSByZWxhdGlvbiBsaW7DqWFpcmUuICBVbiBjb2VmZmljaWVudCBkZSBjb3Jyw6lsYXRpb24gcHJvY2hlIGRlIDEgb3UgLTEgaW5kaXF1ZSB1bmUgZm9ydGUgcmVsYXRpb24gbGluw6lhaXJlLCB0YW5kaXMgcXUndW4gY29lZmZpY2llbnQgcHJvY2hlIGRlIDAgc3VnZ8OocmUgdW5lIGZhaWJsZSBvdSBhdWN1bmUgcmVsYXRpb24gbGluw6lhaXJlLiAgDQoNCkxhIGZvcm11bGUgcG91ciBjYWxjdWxlciBsZSBjb2VmZmljaWVudCBkZSBjb3Jyw6lsYXRpb24gZGUgUGVhcnNvbiwgXChyXCksIGVudHJlIGRldXggdmFyaWFibGVzIFwoWFwpIGV0IFwoWVwpIGVzdCA6DQoNClxbDQpyID0gXGZyYWN7XHN1bSAoWF9pIC0gXG92ZXJsaW5le1h9KShZX2kgLSBcb3ZlcmxpbmV7WX0pfXtcc3FydHtcc3VtIChYX2kgLSBcb3ZlcmxpbmV7WH0pXjIgXHN1bSAoWV9pIC0gXG92ZXJsaW5le1l9KV4yfX0NClxdDQoNCk/DuToNCi0gXChYX2lcKSBldCBcKFlfaVwpIHNvbnQgbGVzIHZhbGV1cnMgaW5kaXZpZHVlbGxlcyBkZXMgdmFyaWFibGVzIFwoWFwpIGV0IFwoWVwpLCAgDQotIFwoXG92ZXJsaW5le1h9XCkgZXQgXChcb3ZlcmxpbmV7WX1cKSBzb250IGxlcyBtb3llbm5lcyBkZSBcKFhcKSBldCBcKFlcKSwgIA0KDQoNCioqTWF0cmljZSBkZSBjb3Jyw6lsYXRpb24qKg0KDQpgYGB7ciwgb3V0LndpZHRoPScxMDAlJ30NCm1jb3IgPC0gY29yKGRhdGFfc2VsZWN0LCANCiAgICAgICAgICAgIHVzZSA9ICJjb21wbGV0ZS5vYnMiLA0KICAgICAgICAgICAgbWV0aG9kID0gJ3BlYXJzb24nKQ0KY29ycnBsb3Q6OmNvcnJwbG90KG1jb3IsIA0KICAgICAgICAgICAgICAgICAgIHR5cGU9InVwcGVyIiwgDQogICAgICAgICAgICAgICAgICAgb3JkZXI9ImhjbHVzdCIsIA0KICAgICAgICAgICAgICAgICAgIHRsLmNvbD0iYmxhY2siKQ0KYGBgDQpMYSBtw6l0aG9kZSBkZSBTcGVhcm1hbiBlc3QgdW5lIG1lc3VyZSBkZSBjb3Jyw6lsYXRpb24gZGUgcmFuZyBxdWkgcGV1dmVudCDDqnRyZSBwbHVzIGFwcHJvcHJpw6llcyBwb3VyIGRlcyBkb25uw6llcyBub24gbm9ybWFsZXMgb3UgcG91ciBkZXMgcmVsYXRpb25zIG5vbiBsaW7DqWFpcmVzLiAgDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KbWNvciA8LSBjb3IoZGF0YV9zZWxlY3QsIA0KICAgICAgICAgICAgdXNlID0gImNvbXBsZXRlLm9icyIsDQogICAgICAgICAgICBtZXRob2QgPSAnc3BlYXJtYW4nKQ0KY29ycnBsb3Q6OmNvcnJwbG90KG1jb3IsIA0KICAgICAgICAgICAgICAgICAgIHR5cGU9InVwcGVyIiwgDQogICAgICAgICAgICAgICAgICAgb3JkZXI9ImhjbHVzdCIsIA0KICAgICAgICAgICAgICAgICAgIHRsLmNvbD0iYmxhY2siKQ0KDQpgYGANCg0KKipBcHByb2NoZSBwb3VyIFLDqWR1aXJlIGxlcyBWYXJpYWJsZXMqKg0KICANCk5vdXMgY29tbWVuw6dvbnMgcGFyIGlkZW50aWZpZXIgbGVzIHZhcmlhYmxlcyBxdWkgb250IGRlcyBjb3Jyw6lsYXRpb25zIHRyw6hzIMOpbGV2w6llcyBhdmVjIGQnYXV0cmVzLCBwb3VyIHLDqWR1aXJlIGxhIHJlZG9uZGFuY2UuIA0KDQoqRm9ydGVzIENvcnLDqWxhdGlvbnMqICANCkRlcyBjb3Jyw6lsYXRpb25zIHRyw6hzIMOpbGV2w6llcyAocHJvY2hlcyBkZSAxIG91IC0xKSBlbnRyZSBkZXV4IHZhcmlhYmxlcyBzdWdnw6hyZW50IHVuZSByZWRvbmRhbmNlIHBvdGVudGllbGxlLiBQYXIgZXhlbXBsZSwgKipzdW1fcG9wdWxhdGlvbioqIGV0ICoqc3VtX3BvcHVsYXRpb25fYWN0aXZlKiogb250IHVuZSBjb3Jyw6lsYXRpb24gZGUgcHJlc3F1ZSAxLCBjZSBxdWkgaW5kaXF1ZSB1bmUgcG9zc2libGUgcmVkb25kYW5jZSBlbnRyZSBjZXMgZGV1eCB2YXJpYWJsZXMuIFNpIHVuZSB2YXJpYWJsZSBlc3QgZm9ydGVtZW50IGNvcnLDqWzDqWUgYXZlYyBwbHVzaWV1cnMgYXV0cmVzIHZhcmlhYmxlcywgY2VsYSBwZXV0IGluZGlxdWVyIHF1J2VsbGUgbidhcHBvcnRlIHBhcyBkJ2luZm9ybWF0aW9ucyB1bmlxdWVzIMOgIGwnZW5zZW1ibGUgZGUgZG9ubsOpZXMuIERhbnMgbm90cmUgY2FzLCBjZXJ0YWluZXMgdmFyaWFibGVzIGNvbW1lICoqbG9uZ3VldXJfcm91dGUqKiBldCAqKm5iX2ludGVyc2VjdGlvbnMqKiBvbnQgZGVzIGNvcnLDqWxhdGlvbnMgw6lsZXbDqWVzIGF2ZWMgcGx1c2lldXJzIGF1dHJlcyB2YXJpYWJsZXMsIHN1Z2fDqXJhbnQgcXUnZWxsZXMgcGFydGFnZW50IGRlcyBpbmZvcm1hdGlvbnMgY29tbXVuZXMuIA0KDQoNCipWYXJpYWJsZXMgw6AgQ29uc2lkw6lyZXIgcG91ciBSw6lkdWN0aW9uKiAgDQpWYXJpYWJsZXMgYXZlYyBmYWlibGUgY29ycsOpbGF0aW9uIGF2ZWMgbGVzIGF1dHJlcyA6IFBhciBleGVtcGxlLCAqKnBhc3NhZ2Vfbml2ZWF1KiogbW9udHJlIGRlcyBjb3Jyw6lsYXRpb25zIHRyw6hzIGZhaWJsZXMgb3UgbsOpZ2F0aXZlcyBhdmVjIGxhIHBsdXBhcnQgZGVzIGF1dHJlcyB2YXJpYWJsZXMsIGNlIHF1aSBwZXV0IHN1Z2fDqXJlciBxdSdlbGxlIGVzdCBtb2lucyBsacOpZSDDoCBsJ2Vuc2VtYmxlIGRlcyB2YXJpYWJsZXMgw6l0dWRpw6llcy4gIA0KDQpOb3VzIHNvdWhhaXRvbnMgbWFpbnRlbmlyIHVuZSBkaXZlcnNpdMOpIGVuIGluY2x1YW50IGRlcyB2YXJpYWJsZXMgcmVwcsOpc2VudGFudCBkaWZmw6lyZW50cyBhc3BlY3RzIGRlIGwndXJiYW5pc21lIGV0IGRlcyBzZXJ2aWNlcywgY29tbWUgcGFyIGV4ZW1wbGUgbGUgbm9tYnJlIGRlIHN0dWN0dXJlcyB0b3VyaXN0aXF1ZXMgb3UgIGxlIG5vbWJyZSBkZSBjb21tZXJjZXMuIEFpbnNpLCBub3VzIGNvbnNlcnZvbnMgOiAgDQo8YnI+DQoNCiogUG9wdWxhdGlvbiB0b3RhbGUgOiBQb3VyIHJlcHLDqXNlbnRlciBsYSBkw6ltb2dyYXBoaWUgIA0KKiBOb21icmUgZGUgc3RydWN0dXJlcyBkZSB0b3VyaXNtZSA6IFBvdXIgw6l2YWx1ZXIgbCdhY2PDqHMgYXV4IHNvaW5zIGVzcGFjZXMgZGUgbG9pc2lycyAgDQoqIExlcyBhcnLDqnRzIGRlIHRyYW5zcG9ydCBlbiBjb21tdW4gOiBSZWZsw6h0ZSBsJ2FjY2Vzc2liaWxpdMOpIGV0IGxhIHF1YWxpdMOpIGRlIGwnaW5mcmFzdHJ1Y3R1cmUgZGUgdHJhbnNwb3J0IHB1YmxpYywgdW4gZmFjdGV1ciBpbXBvcnRhbnQgcG91ciBsYSBtb2JpbGl0w6kgdXJiYWluZSBldCBww6lyaXVyYmFpbmUgICANCiogTm9tYnJlIGRlIGNvbW1lcmNlcyA6IFBvdXIgcmVmbMOpdGVyIGwnYWN0aXZpdMOpIMOpY29ub21pcXVlIGxvY2FsZSAgDQoqIE5vbWJyZSBkJ8OpbMOodmVzIDogRG9ubmUgdW5lIGlkw6llIGRlIGxhIHBvcHVsYXRpb24gc2NvbGFpcmUsIHBlcnRpbmVudCBwb3VyIMOpdmFsdWVyIGxlcyBiZXNvaW5zIGVuIMOpZHVjYXRpb24gZXQgbGVzIGR5bmFtaXF1ZXMgamV1bmVzc2UgZHUgdGVycml0b2lyZSAgDQoqIExlIG5vbWJyZSBkZSBwYXNzYWdlIMOgIG5pdmVhdSA6IFNpZ25lIGRlIGwnaW50ZXJjb25uZXhpb24gZW50cmUgbGUgcsOpc2VhdSBmZXJyb3ZpYWlyZSBldCBsYSB0cmFtZSB1cmJhaW5lLCBpbXBvcnRhbnQgcG91ciBjb21wcmVuZHJlIGxlcyBlbmpldXggZGUgbW9iaWxpdMOpIGV0IGRlIHPDqWN1cml0w6kgIA0KKiBMZXMgem9uZXMgYXJ0aWZpY2lhbGlzw6llcyA6IFBvdXIgbWVzdXJlciBsZSBwb3RlbnRpZWwgdXJiYWluICANCiogTGEgcGVudGUgKGRhbnMgbGVzIGRvbm7DqWVzIHN1ciBsZSB2w6lsbykgOiDDiXZhbHVhdGlvbiBkZSBsYSBkaWZmaWN1bHTDqSBkZSBkw6lwbGFjZW1lbnQgZW4gdsOpbG8sIHVuIGFzcGVjdCBmb25kYW1lbnRhbCBwb3VyIHByb21vdXZvaXIgbGEgbW9iaWxpdMOpIGRvdWNlIGV0IHBsYW5pZmllciBkZXMgaW5mcmFzdHJ1Y3R1cmVzIGN5Y2xhYmxlcyBhZGFwdMOpZXMgIA0KDQoNCioqVGFibGVhdSBkZXMgdmFyaWFibGVzIHJldGVudWVzKiogIA0KPGJyPg0KPGNlbnRlcj4NCiFbXShpbWFnZXMvZGF0YV90YWJsZV9hbGxlZ2VlLnBuZykgIA0KKlRhYmxlYXUgMSA6IExpc3RlIGRlcyB2YXJpYWJsZXMgc8OpbGVjdGlvbm7DqWVzKiAgDQo8L2NlbnRlcj4NCjxicj4NCjxicj4NCg0KDQoqKlZhcmlhbmNlIGluZmxhdGlvbiBmYWN0b3IgKFZJRikqKg0KDQpMZSBWSUYgcXVhbnRpZmllIGNvbWJpZW4gbGEgdmFyaWFuY2UgZGVzIGNvZWZmaWNpZW50cyBkZSByw6lncmVzc2lvbiBlc3QgYXVnbWVudMOpZSBlbiByYWlzb24gZGUgbGEgY29saW7DqWFyaXTDqS4gSWwgZXN0IHV0aWxpc8OpIHBvdXIgZMOpdGVjdGVyIGxhIG11bHRpY29saW7DqWFyaXTDqSBlbnRyZSBwbHVzaWV1cnMgdmFyaWFibGVzIGluZMOpcGVuZGFudGVzLiAgDQoNCklsIHBlcm1ldCBkZSBkw6l0ZWN0ZXIgc2kgMiB2YWxldXJzIGNvbnRpZW5uZW50IGxlcyBtw6ptZXMgaW5mb3JtYXRpb25zLiBTaSBjJ2VzdCBsZSBjYXMsIGlsIGVzdCBwb3NzaWJsZSBkZSBuJ2VuIGNvbnNlcnZlciBxdSd1bmUgc2V1bGUgcG91ciBsaW1pdGVyIGxhIGNvbGluw6lhcml0w6kgZXQgc29uIGluZmx1ZW5jZSBzdXIgbGEgdmFyaWFuY2UgdG90YWxlLiANCg0KTCfDqXF1YXRpb24gZHUgVmFyaWFuY2UgSW5mbGF0aW9uIEZhY3RvciAoVklGKSBlc3QgZG9ubsOpZSBwYXIgOg0KDQpcWw0KXHRleHR7VklGfV9pID0gXGZyYWN7MX17MSAtIFJfaV4yfQ0KXF0NCg0Kb8O5IDogIA0KLSBcKCBcdGV4dHtWSUZ9X2kgXCkgZXN0IGxlIFZhcmlhbmNlIEluZmxhdGlvbiBGYWN0b3IgcG91ciBsZSBcKCBpIFwpLcOobWUgcHLDqWRpY3RldXIuICANCi0gXCggUl9pXjIgXCkgZXN0IGxlIGNvZWZmaWNpZW50IGRlIGTDqXRlcm1pbmF0aW9uIG9idGVudSBlbiByw6lncmVzc2FudCBsZSBcKCBpIFwpLcOobWUgcHLDqWRpY3RldXIgc3VyIHRvdXMgbGVzIGF1dHJlcyBwcsOpZGljdGV1cnMgZHUgbW9kw6hsZS4gIA0KDQpDZXR0ZSDDqXF1YXRpb24gbW9udHJlIHF1ZSBsZSBWSUYgbWVzdXJlIGwnaW5mbGF0aW9uIGRlIGxhIHZhcmlhbmNlIGQndW4gY29lZmZpY2llbnQgZGUgcsOpZ3Jlc3Npb24gZW4gcmFpc29uIGRlIGxhIGNvbGluw6lhcml0w6kgZW50cmUgbGVzIHByw6lkaWN0ZXVycy4NCg0KDQojIyBBQ1ANCg0KUmFwcGVsIHN1ciBs4oCZQUNQLiAgDQoNCkzigJkqKmFuYWx5c2UgbXVsdGl2YXJpw6llKiogcGVybWV0IGTigJnDqXR1ZGllciBsZXMgcmVsYXRpb25zIGVudHJlIHBsdXNpZXVycyB2YXJpYWJsZXMgZXQgZGlzcG9zZSBkZSBwbHVzaWV1cnMgb3V0aWxzIHN0YXRpc3RpcXVlcy4NCg0KTGVzICoqYW5hbHlzZXMgZmFjdG9yaWVsbGVzKiogZm9udCBwYXJ0aWUgZGUgY2VzIG91dGlscy4gICAgDQo0IGdyYW5kcyB0eXBlcyBwZXV2ZW50IMOqdHJlIHV0aWxpc8OpcyA6ICANCiogbCdhbmFseXNlIGVuIGNvbXBvc2FudGVzIHByaW5jaXBhbGVzIChBQ1ApIDogTCdBQ1AgZXN0IHV0aWxlIGZhY2Ugw6AgZGVzIHZhcmlhYmxlcyBxdWFudGl0YXRpdmVzICANCiogbCdhbmFseXNlIGZhY3RvcmllbGxlIGRlcyBjb3JyZXNwb25kYW5jZXMgKEFGQykgOiBMJ0FGQyBlc3QgdXRpbGUgZmFjZSDDoCBkZXV4IHZhcmlhYmxlcyBxdWFsaXRhdGl2ZXMgIA0KKiBsJ2FuYWx5c2UgZGVzIGNvcnJlc3BvbmRhbmNlcyBtdWx0aXBsZXMgKEFDTSkgOiBMJ0FDTSBlc3QgdXRpbGUgZmFjZSDDoCBwbHVzaWV1cnMgdmFyaWFibGVzIHF1YWxpdGF0aXZlcyAgDQoqIGwnYW5hbHlzZSBmYWN0b3JpZWxsZSBkZXMgY29ycmVzcG9uZGFuY2VzIG1peHRlcyBvdSBkZXMgZG9ubsOpZXMgbWl4dGVzIChBRkNNIG91IEFGRE0pIDogTCdBRkNNIHByZW5kIGVuIGNvbXB0ZSDDoCBsYSBmb2lzIGRlcyB2YXJpYWJsZXMgcXVhbnRpdGF0aXZlcyBldCBxdWFsaXRhdGl2ZXMNCiAgDQpBaW5zaSwgbOKAmWFuYWx5c2UgZW4gY29tcG9zYW50ZXMgcHJpbmNpcGFsZXMgKEFDUCkgcGVybWV0IGRlIHLDqXN1bWVyIGzigJlpbmZvcm1hdGlvbiBkZSBwbHVzaWV1cnMgdmFyaWFibGVzIHF1YW50aXRhdGl2ZXMuIEzigJlpbmZvcm1hdGlvbiBlc3QgcsOpc3Vtw6llIGVuIHVuIHBsdXMgcGV0aXQgbm9tYnJlIGRlIOKAnGNvbXBvc2FudGVz4oCdLCBxdWkgc29udCBkZXMgY29tYmluYWlzb25zIGRlcyB2YXJpYWJsZXMgaW5pdGlhbGVzLiBMZXMgY29tcG9zYW50ZXMgb2J0ZW51ZXMgc29udCBub24tY29ycsOpbMOpZXMgZW50cmUgZWxsZXMuDQogIA0KUG91ciByw6lhbGlzZXIgbOKAmUFDUCBub3VzIHV0aWxpc29ucyBsYSBtw6l0aG9kZSBkdSBwYWNrYWdlIEZhY3RvbWluZVIuICAgDQpOb3VzIHV0aWxpc29ucyDDqWdhbGVtZW50IGxlIHBhY2thZ2UgZmFjdG9leHRyYSBwb3VyIGxhIHJlcHLDqXNlbnRhdGlvbiBncmFwaGlxdWUuICAgDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBQYWNrYWdlcw0KcGFjbWFuOjpwX2xvYWQoc2YsIGRwbHlyLCBGYWN0b01pbmVSLCBmYWN0b2V4dHJhKQ0KDQojIERhdGENCmFsbF9kYXRhPC0gc2Y6OnN0X3JlYWQoJ3Byb2Nlc3NlZF9kYXRhL2FsbF9kYXRhX3N0YW5kYXJkaXplZF9zdHBvbF9mb290XzEwbWluX3BvcF9jYXJyZWF1XzIwMjQwMzA3Lmdwa2cnKQ0KbmFtZXMoYWxsX2RhdGEpDQpkYXRhX3NlbGVjdCA8LSBhbGxfZGF0YSAlPiUgDQogIHNlbGVjdChzdW1fcG9wdWxhdGlvbiwNCiAgICAgICAgIHN1bV9wb3B1bGF0aW9uX2FjdGl2ZSwNCiAgICAgICAgIHN1bV9saXRzLA0KICAgICAgICAgbG9uZ3VldXJfcm91dGUsDQogICAgICAgICBuYl9pbnRlcnNlY3Rpb25zLA0KICAgICAgICAgcmVzZWF1X3BlZGVzdHJlLA0KICAgICAgICAgbG9uZ3VldXJfcGlzdGVzX2N5Y2xhYmxlcywNCiAgICAgICAgIG5vbWJyZV9hcnJldHMsDQogICAgICAgICBub21icmVfcGFya2luZ3MsDQogICAgICAgICBub21icmVfY29tbWVyY2VzLA0KICAgICAgICAgbm9tYnJlX3NhbnRlLA0KICAgICAgICAgbm9tYnJlX2xvaXNpcnMsDQogICAgICAgICBub21icmVfcmVzdGF1cmF0aW9uLA0KICAgICAgICAgbm9tYnJlX3Nwb3J0cywNCiAgICAgICAgIG5vbWJyZV9yb25kc19wb2ludHMsDQogICAgICAgICBub21icmVfZWxldmVzLA0KICAgICAgICAgcGFzc2FnZV9uaXZlYXUsDQogICAgICAgICBaQSkgJT4lIA0KICBzdF9kcm9wX2dlb21ldHJ5KCkNCmdsaW1wc2UoZGF0YV9zZWxlY3QpDQoNCiMgQ29lZmZpY2llbnQgZGUgY29ycsOpbGF0aW9uDQpzdGF0czo6Y29yKGRhdGFfc2VsZWN0LCB1c2UgPSAiY29tcGxldGUub2JzIikNCmBgYA0KDQoNCmBgYHtyLCBldmFsID0gVCwgZWNobyA9IFQsIGZpZy5zaG93PSJoaWRlIiwgb3V0LndpZHRoPScxMDAlJ30NCiMgTGFuY2VtZW50IGRlIGwnQUNQDQpQQ0EgPC0gUENBKGRhdGFfc2VsZWN0LCBzY2FsZS51bml0ID0gVCkNCmBgYA0KDQpgYGB7ciwgZXZhbCA9IFQsIGVjaG8gPSBULCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBwb2lkcyBkZSBjaGFxdWUgY29tcG9zYW50ZQ0KZnZpel9laWcoUENBLCBhZGRsYWJlbHMgPSBUUlVFLCB5bGltID0gYygwLCA2MCkpDQoNCiMgQ2VyY2xlIGRlcyBjb3Jyw6lsYXRpb25zDQpmdml6X3BjYV92YXIoUENBLCBjb2wudmFyPSJjb250cmliIiwNCiAgICAgICAgICAgICBncmFkaWVudC5jb2xzID0gYygiIzAwQUZCQiIsICIjRTdCODAwIiwgIiNGQzRFMDciKSwNCiAgICAgICAgICAgICByZXBlbCA9IFRSVUUpDQoNCiMgR3JhcGhpcXVlIGRlcyBpbmRpdmlkdXMNCmZ2aXpfcGNhX2luZChQQ0EsIGNvbC5pbmQgPSAiY29zMiIsDQogICAgICAgICAgICAgZ3JhZGllbnQuY29scyA9IGMoIiMwMEFGQkIiLCAiI0U3QjgwMCIsICIjRkM0RTA3IiksDQogICAgICAgICAgICAgcmVwZWwgPSBUUlVFKQ0KDQoNCiMgVGFibGVhdSBkZXMgdmFsZXVycyBwcm9wcmVzDQpQQ0EkZWlnDQoNCiMgQ29udHJpYnV0aW9uIGRlIGNoYXF1ZSB2YXJpYWJsZSBhdXggdHJvaXMgcHJlbWllcnMgYXhlcw0KZnZpel9jb250cmliKFBDQSwgY2hvaWNlID0gInZhciIsIGF4ZXMgPSAxKSAjIGF4ZSAxDQpmdml6X2NvbnRyaWIoUENBLCBjaG9pY2UgPSAidmFyIiwgYXhlcyA9IDIpICMgYXhlIDINCmZ2aXpfY29udHJpYihQQ0EsIGNob2ljZSA9ICJ2YXIiLCBheGVzID0gMykgIyBheGUgMw0KDQojIENvbnRyaWJ1dGlvbiBkZSBjaGFxdWUgaW5kaXZpZHUgYXV4IGRldXggcHJlbWllcnMgYXhlcw0KZnZpel9jb250cmliKFBDQSwgY2hvaWNlID0gImluZCIsIGF4ZXMgPSAxKQ0KZnZpel9jb250cmliKFBDQSwgY2hvaWNlID0gImluZCIsIGF4ZXMgPSAyKQ0KZnZpel9jb250cmliKFBDQSwgY2hvaWNlID0gImluZCIsIGF4ZXMgPSAzKQ0KYGBgDQoNCiMjIE1VTFRJTklWRUFVWA0KDQpgYGB7cn0NCiMgcGFja2FnZXMgLS0tLQ0KcGFjbWFuOjpwX2xvYWQoZHBseXIsIGx1YnJpZGF0ZSwgcmVhZHIsIGxtZTQsIE1hdHJpeCkNCmBgYA0KPGJyPg0KDQoqKlZhcmlhYmxlcyDDqXR1ZGnDqWVzIHBhciBuaXZlYXUqKiAgDQoNCk5JVkVBVSAyIDogIGxpZ25lcyBkZSB0cmFpbiBhdmVjIDogICANCiogbm9tYnJlIGQnYXJyw6p0cyAgDQoqIHRlbXBzIG1veWVuIGR1IHRyYWpldCBlbnRyZSBsYSBnYXJlIGRlIGTDqXBhcnQgZXQgbGEgZ2FyZSBkJ2Fycml2w6llDQoqIGxvbmd1ZXVyIGRlIGxhIGxpZ25lICANCiogbm9tYnJlIGRlIHRyYWlucyBwYXIgam91ciwgw6AgcGFydGlyIGRlcyBkb25uw6llcyBHVEZTICAgDQoqIG5vbWJyZSBkJ2luY2lkZW50cyA/ICDDoCBwYXJ0aXIgZGUgcXVlbGxlIGJhc2UgPyAgICANCjxicj4NCiAgDQpOSVZFQVUgMSA6IGdhcmVzIGF2ZWMgOiAgDQoqIHBvcHVsYXRpb24gw6AgMTAgbWludXRlcyBlbiB2b2l0dXJlID8NCiogaW5mb3MgdG91cmlzbWUgIA0KKiBhcnLDqnRzIGRlIHRyYW5zcG9ydCDDoCBwcm94aW1pdMOpIMOgIDEwIG1pbnV0ZXMgw6AgcGllZCA/IA0KKiBjb21tZXJjZXMgw6AgMTAgbWludXRlcyDDoCBwaWVkID8gIA0KKiBub21icmUgZCfDqWzDqHZlcyAgw6AgMTAgbWludXRlcyDDoCB2w6lsbyA/ICANCiogem9uZXMgYXJ0aWZpY2llbGxlcyDDoCAxMCBtaW51dGVzIMOgIHBpZWQgPyAgDQoqIHBhc3NhZ2VzIMOgIG5pdmVhdSAgw6AgMTAgbWludXRlcyDDoCBwaWVkID8gIA0KPGJyPiAgDQoNCiMjIyBUQUJMRUFVIERFUyBMSUdORVMgRkVSUk9WSUFJUkVTIChuaXZlYXUgMikNCg0KSWNpIGplIGNhbGN1bGUgbGUgdGVtcHMgbW95ZW4gZCd1biB0cmFqZXQgZW50cmUgbGEgZ2FyZSBkZSBkw6lwYXJ0IGV0IGxhIGdhcmUgZCdhcnJpdsOpZS4gSmUgY29tcHRlIMOpZ2FsZW1lbnQgbGUgbm9tYnJlIGQnYXJyw6p0cyBwYXIgbGlnbmUuICAgDQo8YnI+DQoNCmBgYHtyfQ0KIyB0ZW1wcyBtb3llbiBwb3VyIHRvdXRlcyBsZXMgbGlnbmVzIC0tLS0NCg0KIyBDaGFyZ2VyIGxlcyBkb25uw6llcw0KDQojIyBJdGluw6lyYWlyZXMgZGUgdHJhbnNwb3J0IGVuIGNvbW11bi4gRXggOiBQYXJpcyBNb250cGFybmFzc2UgLSBUb3Vsb3VzZSBNYXRhYmlhdQ0Kcm91dGVzIDwtIHJlYWQuY3N2KCdkYXRhL0dURlMvZXhwb3J0LXRlci1ndGZzLWxhc3Qvcm91dGVzLnR4dCcsIGhlYWRlciA9IFRSVUUpICU+JSANCiAgZmlsdGVyKHJvdXRlX3R5cGUgPT0gMikgIyAwID0gVHJhbS9UcmFtd2F5L1RyYWluIGzDqWdlciA7ICMgMSA9IE3DqXRybyA7IDIgPSBSYWlscyA7IDMgPSBCdXMgOyA0ID0gRmVycnkNCg0KIyMgCVRyYWpldHMgcG91ciBjaGFxdWUgbGlnbmUuIA0KIyMgVW4gdHJhamV0IGVzdCB1bmUgc8OpcXVlbmNlIGRlIGRldXggYXJyw6p0cyBvdSBwbHVzIHF1aSBzZSBwcm9kdWlzZW50IHBlbmRhbnQgdW5lIHDDqXJpb2RlIGRlIHRlbXBzIHNww6ljaWZpcXVlDQp0cmlwcyA8LSByZWFkLmNzdignZGF0YS9HVEZTL2V4cG9ydC10ZXItZ3Rmcy1sYXN0L3RyaXBzLnR4dCcsIGhlYWRlciA9IFRSVUUpDQoNCiMjIExlcyBoZXVyZXMgZCdhcnJpdsOpZSBldCBkZSBkw6lwYXJ0IGQndW4gdsOpaGljdWxlIGF1eCBhcnLDqnRzIHBvdXIgY2hhcXVlIHRyYWpldC4NCnN0b3BfdGltZXMgPC0gcmVhZC5jc3YoJ2RhdGEvR1RGUy9leHBvcnQtdGVyLWd0ZnMtbGFzdC9zdG9wX3RpbWVzLnR4dCcsIGhlYWRlciA9IFRSVUUpDQoNCg0KIyBkYXRhZnJhbWUgcG91ciBzdG9ja2VyIGxlcyBkdXLDqWVzIG1veWVubmVzIHBhciByb3V0ZSBlbnRyZSBwb2ludCBkZSBkw6lwYXJ0IGV0IGQnYXJyaXbDqWUNCmF2ZXJhZ2VfZHVyYXRpb25zIDwtIGRhdGEuZnJhbWUocm91dGVfaWQgPSBjaGFyYWN0ZXIoKSwgDQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGF2ZXJhZ2VfdGltZSA9IG51bWVyaWMoKSkNCg0KIyBCb3VjbGUgc3VyIGNoYXF1ZSByb3V0ZV9pZCBkYW5zIHJvdXRlcw0KZm9yKHJvdXRlX2lkX3NlbGVjdCBpbiB1bmlxdWUoYXMuY2hhcmFjdGVyKHJvdXRlcyRyb3V0ZV9pZCkpKSB7DQogIA0KICAjIEZpbHRyZSBsZXMgdHJhamV0cyBwb3VyIGxhIHJvdXRlIGFjdHVlbGxlDQogIGZpbHRlcmVkX3RyaXBzIDwtIHRyaXBzICU+JQ0KICAgIGZpbHRlcihyb3V0ZV9pZCA9PSByb3V0ZV9pZF9zZWxlY3QpDQogIA0KICAjIEV4dHJhY3Rpb24gZHUgbm9tIGRlIGxhIHJvdXRlDQogIHJvdXRlc19maWx0ZXIgPC0gZmlsdGVyZWRfdHJpcHMkcm91dGVfaWRbMV0NCiAgcm91dGVfbG9uZ19uYW1lIDwtIHJvdXRlcyAlPiUgDQogICAgZmlsdGVyKHJvdXRlX2lkID09IHJvdXRlc19maWx0ZXIpDQogIHJvdXRlX2xvbmdfbmFtZSA8LSByb3V0ZV9sb25nX25hbWUkcm91dGVfbG9uZ19uYW1lDQogIA0KICAjIEZpbHRyZSBsZXMgc3RvcF90aW1lcyBwb3VyIGxlcyB0cmFqZXRzIGZpbHRyw6lzDQogIHN0b3BfdGltZXNfZmlsdGVyZWQgPC0gc3RvcF90aW1lcyAlPiUNCiAgICBmaWx0ZXIodHJpcF9pZCAlaW4lIGZpbHRlcmVkX3RyaXBzJHRyaXBfaWQpICU+JQ0KICAgIGFycmFuZ2UodHJpcF9pZCwgYXJyaXZhbF90aW1lKSAlPiUNCiAgICBzZWxlY3QodHJpcF9pZCwgc3RvcF9pZCwgYXJyaXZhbF90aW1lLCBkZXBhcnR1cmVfdGltZSkNCiAgDQogICMgQ2FsY3VsZXIgbGEgZHVyw6llIGRlIGNoYXF1ZSB2b3lhZ2UNCiAgdHJpcF9kdXJhdGlvbnMgPC0gc3RvcF90aW1lc19maWx0ZXJlZCAlPiUNCiAgICBncm91cF9ieSh0cmlwX2lkKSAlPiUNCiAgICBzdW1tYXJpc2UoDQogICAgICBzdGFydF90aW1lID0gZmlyc3QoZGVwYXJ0dXJlX3RpbWUpLA0KICAgICAgZW5kX3RpbWUgPSBsYXN0KGFycml2YWxfdGltZSksDQogICAgICBkdXJhdGlvbiA9IGFzLm51bWVyaWMoaG1zKGVuZF90aW1lKSAtIGhtcyhzdGFydF90aW1lKSwgdW5pdHMgPSAibWlucyIpDQogICAgKQ0KICANCiAgIyBDYWxjdWxlIGxhIGR1csOpZSBtb3llbm5lIHBvdXIgbGEgcm91dGUgYWN0dWVsbGUNCiAgYXZlcmFnZV9kdXJhdGlvbiA8LSB0cmlwX2R1cmF0aW9ucyAlPiUNCiAgICBzdW1tYXJpc2UoYXZlcmFnZV90aW1lID0gbWVhbihkdXJhdGlvbiwgbmEucm0gPSBUUlVFKSkNCiAgDQogICMgQWpvdXQgZHUgcsOpc3VsdGF0IGRhbnMgbGUgZGF0YWZyYW1lIGRlcyBkdXLDqWVzIG1veWVubmVzDQogIGF2ZXJhZ2VfZHVyYXRpb25zIDwtIHJiaW5kKGF2ZXJhZ2VfZHVyYXRpb25zLCBkYXRhLmZyYW1lKHJvdXRlX2lkID0gcm91dGVfaWRfc2VsZWN0LCANCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgcm91dGVfbmFtZSA9IHJvdXRlX2xvbmdfbmFtZSwNCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgYXZlcmFnZV90aW1lID0gYXZlcmFnZV9kdXJhdGlvbiRhdmVyYWdlX3RpbWUpKQ0KfQ0KDQojIEFmZmljaGUgbGVzIGR1csOpZXMgbW95ZW5uZXMgcG91ciB0b3V0ZXMgbGVzIHJvdXRlcw0KaGVhZChhdmVyYWdlX2R1cmF0aW9ucykNCmBgYA0KDQoNCmBgYHtyfQ0KIyBub21icmUgZGUgc3RvcHMgcGFyIGxpZ25lcyAocm91dGVzKSAtLS0tDQoNCiMgQ2hhcmdlciBsZXMgZG9ubsOpZXMNCg0KIyMgSXRpbsOpcmFpcmVzIGRlIHRyYW5zcG9ydCBlbiBjb21tdW4uIEV4IDogUGFyaXMgTW9udHBhcm5hc3NlIC0gVG91bG91c2UgTWF0YWJpYXUNCnJvdXRlcyA8LSByZWFkLmNzdignZGF0YS9HVEZTL2V4cG9ydC10ZXItZ3Rmcy1sYXN0L3JvdXRlcy50eHQnLCBoZWFkZXIgPSBUUlVFKSAlPiUgDQogIGZpbHRlcihyb3V0ZV90eXBlID09IDIpICMgMCA9IFRyYW0vVHJhbXdheS9UcmFpbiBsw6lnZXIgOyAjIDEgPSBNw6l0cm8gOyAyID0gUmFpbHMgOyAzID0gQnVzIDsgNCA9IEZlcnJ5DQoNCiMjIFRyYWpldHMgcG91ciBjaGFxdWUgbGlnbmUNCiMjIFVuIHRyYWpldCBlc3QgdW5lIHPDqXF1ZW5jZSBkZSBkZXV4IGFycsOqdHMgb3UgcGx1cyBxdWkgc2UgcHJvZHVpc2VudCBwZW5kYW50IHVuZSBww6lyaW9kZSBkZSB0ZW1wcyBzcMOpY2lmaXF1ZQ0KdHJpcHMgPC0gcmVhZC5jc3YoJ2RhdGEvR1RGUy9leHBvcnQtdGVyLWd0ZnMtbGFzdC90cmlwcy50eHQnLCBoZWFkZXIgPSBUUlVFKQ0KDQojIyBBcnLDqnRzIG/DuSBsZXMgdsOpaGljdWxlcyBwcmVubmVudCBvdSBkw6lwb3NlbnQgbGVzIHVzYWdlcnMuIA0KIyMgRMOpZmluaXQgw6lnYWxlbWVudCBsZXMgc3RhdGlvbnMgZXQgbGVzIGVudHLDqWVzIGRlIHN0YXRpb24uDQpzdG9wcyA8LSByZWFkLmNzdignZGF0YS9HVEZTL2V4cG9ydC10ZXItZ3Rmcy1sYXN0L3N0b3BzLnR4dCcsIGhlYWRlciA9IFRSVUUpDQoNCiMgSm9pbmRyZSB0cmlwcyDDoCByb3V0ZXMNCnRyaXBzX3dpdGhfcm91dGVzIDwtIHRyaXBzICU+JQ0KICBpbm5lcl9qb2luKHJvdXRlcywgYnkgPSAicm91dGVfaWQiKQ0KDQojIEpvaW5kcmUgc3RvcF90aW1lcyDDoCB0cmlwc193aXRoX3JvdXRlcw0Kc3RvcHNfd2l0aF9yb3V0ZXMgPC0gc3RvcF90aW1lcyAlPiUNCiAgaW5uZXJfam9pbih0cmlwc193aXRoX3JvdXRlcywgYnkgPSAidHJpcF9pZCIpDQoNCnN0b3BzX3Blcl9yb3V0ZSA8LSBzdG9wc193aXRoX3JvdXRlcyAlPiUNCiAgZ3JvdXBfYnkocm91dGVfaWQpICU+JQ0KICBzdW1tYXJpc2UobnVtYmVyX29mX3N0b3BzID0gbl9kaXN0aW5jdChzdG9wX2lkKSkNCg0KaGVhZChzdG9wc19wZXJfcm91dGUpDQpgYGANCg0KDQpgYGB7cn0NCiMgRnVzaW9uIGRlcyBkZXV4IGRhdGEgZnJhbWVzIHN1ciBsYSBjb2xvbm5lICdyb3V0ZV9pZCcNCm1lcmdlZF9kYXRhIDwtIG1lcmdlKGF2ZXJhZ2VfZHVyYXRpb25zLCBzdG9wc19wZXJfcm91dGUsIGJ5ID0gInJvdXRlX2lkIikNCg0KIyBBZmZpY2hhZ2UgZGVzIHByZW1pw6hyZXMgbGlnbmVzIGR1IGRhdGEgZnJhbWUgZnVzaW9ubsOpDQpoZWFkKG1lcmdlZF9kYXRhKQ0KbmFtZXMobWVyZ2VkX2RhdGEpDQpgYGANCg0KUG9pbnQgw6l0YXBlIDogaWNpIGonYWkgZG9uYyBsZXMgbGlnbmVzIGF2ZWMgbGV1ciB0ZW1wcyBtb3llbiBkZSB0cmFqZXQgZW50cmUgbGUgZMOpcGFydCBldCBsJ2Fycml2w6llIGV0IGxlIG5vbWJyZSBkJ2FycsOqdHMgcG91ciBjaGFxdWUgdHJhamV0Lg0KDQo8YnI+DQoNCg0KIyMjIFRBQkxFQVUgREVTIEdBUkVTIChuaXZlYXUgMSkNCg0KYGBge3J9DQojIGNyw6lhdGlvbiBkdSB0YWJsZWF1IHJvdXRlX2lkLCBzdG9wc19pZCwgc3RvcF9uYW1lIC0tLS0NCg0Kc3RvcHMgPC0gcmVhZC5jc3YoJ2RhdGEvR1RGUy9leHBvcnQtdGVyLWd0ZnMtbGFzdC9zdG9wcy50eHQnLCBoZWFkZXIgPSBUUlVFKQ0Kc3RvcF90aW1lcyA8LSByZWFkLmNzdignZGF0YS9HVEZTL2V4cG9ydC10ZXItZ3Rmcy1sYXN0L3N0b3BfdGltZXMudHh0JywgaGVhZGVyID0gVFJVRSkNCnRyaXBzIDwtIHJlYWQuY3N2KCdkYXRhL0dURlMvZXhwb3J0LXRlci1ndGZzLWxhc3QvdHJpcHMudHh0JywgaGVhZGVyID0gVFJVRSkNCnJvdXRlcyA8LSByZWFkLmNzdignZGF0YS9HVEZTL2V4cG9ydC10ZXItZ3Rmcy1sYXN0L3JvdXRlcy50eHQnLCBoZWFkZXIgPSBUUlVFKQ0KDQojIEpvaW5kcmUgbGVzIGRhdGEgZnJhbWVzIHN1ciAnc3RvcF9pZCcNCmpvaW5lZF9kYXRhIDwtIG1lcmdlKHN0b3BfdGltZXMsIHN0b3BzLCBieSA9ICJzdG9wX2lkIikNCg0KIyBmaW5hbF90YWJsZSA8LSBqb2luZWRfZGF0YSAlPiUNCiMgICBncm91cF9ieSh0cmlwX2lkKSAlPiUNCiMgICBzdW1tYXJpc2UoDQojICAgICB0cmlwX2lkID0gcGFzdGUodW5pcXVlKHRyaXBfaWQpLCBjb2xsYXBzZSA9ICIsICIpLA0KIyAgICAgc3RvcHNfbmFtZSA9IHBhc3RlKHVuaXF1ZShzdG9wX25hbWUpLCBjb2xsYXBzZSA9ICIsICIpDQojICAgKQ0KDQojIEpvaW5kcmUgbGVzIGRhdGEgZnJhbWVzIHN1ciAndHJpcF9pZCcNCmpvaW5lZF9kYXRhXzIgPC0gbWVyZ2UodHJpcHMsIGpvaW5lZF9kYXRhLCBieSA9ICJ0cmlwX2lkIikNCg0KIyBmaW5hbF90YWJsZV8yIDwtIGpvaW5lZF9kYXRhXzIgJT4lDQojICAgZ3JvdXBfYnkodHJpcF9pZCkgJT4lDQojICAgc3VtbWFyaXNlKA0KIyAgICAgdHJpcF9pZCA9IHBhc3RlKHVuaXF1ZSh0cmlwX2lkKSwgY29sbGFwc2UgPSAiLCAiKSwNCiMgICAgIHJvdXRlX2lkID0gcGFzdGUodW5pcXVlKHJvdXRlX2lkKSwgY29sbGFwc2UgPSAiLCAiKQ0KIyAgICkNCg0KIyBKb2luZHJlIGxlcyBkYXRhIGZyYW1lcyBzdXIgJ3N0b3BfaWQnDQpqb2luZWRfZGF0YV8zIDwtIG1lcmdlKHJvdXRlcywgam9pbmVkX2RhdGFfMiwgYnkgPSAicm91dGVfaWQiKQ0KDQpmaW5hbF90YWJsZSA8LSBqb2luZWRfZGF0YV8zICU+JQ0KICBncm91cF9ieShzdG9wX2lkKSAlPiUNCiAgc3VtbWFyaXNlKA0KICAgIHN0b3BfaWQgPSBwYXN0ZSh1bmlxdWUoc3RvcF9pZCksIGNvbGxhcHNlID0gIiwgIiksDQogICAgcm91dGVfaWQgPSBwYXN0ZSh1bmlxdWUocm91dGVfaWQpLCBjb2xsYXBzZSA9ICIsICIpLA0KICAgIHN0b3BfbmFtZSA9IHBhc3RlKHVuaXF1ZShzdG9wX25hbWUpLCBjb2xsYXBzZSA9ICIsICIpDQogICkNCg0KZmluYWxfdGFibGVfZmlsdGVyIDwtIGZpbmFsX3RhYmxlICU+JSANCiAgZmlsdGVyKGdyZXBsKCdUcmFpbicsIHN0b3BfaWQpKQ0KYGBgDQoNCkljaSBqZSByZWN1cMOocmUgbGVzIElEIGRlcyByb3V0ZXMgYXZlYyBsZXMgSUQgZGVzIGFycsOqdHMgZXQgbGV1cnMgbm9tcw0KDQpgYGB7cn0NCmhlYWQoZmluYWxfdGFibGVfZmlsdGVyKQ0KYGBgDQoNCg0KYGBge3IsIG91dC53aWR0aD0nMTAwJSd9DQojIENoYXJnZW1lbnQgZGVzIGRhdGEgDQoNCiMgbWVzIGRvbm7DqWVzIHN1ciBsZXMgZ2FyZXMgOiBjYWxjdWxzIGRlIHZhcmlhYmxlcyBwb3VyIGRlcyBpc29zaHJvbmVzIDE1IG1pbnV0ZXMgw6AgcGllZCBzdXIgbGVzIDQwMCBnYXJlcyBkZXMgSGF1dHMtZGUtRnJhbmNlDQpnYXJlc19IREYgPC0gc2Y6OnN0X3JlYWQoJ3Byb2Nlc3NlZF9kYXRhL2dhcmVzX0hEUl9qb2luX3JlZ2lvbl9IREZfZm9vdF9wMTVfMjAyNDAyMTQuZ3BrZycpDQoNCmdhcmVzX0hERiA8LSBnYXJlc19IREYgJT4lIA0KICByZW5hbWUoc3RvcF9uYW1lID0gSURfbnVtYmVyKQ0KDQpnYXJlc19IREZfbWVyZ2UgPC0gbWVyZ2UoZ2FyZXNfSERGLCBmaW5hbF90YWJsZV9maWx0ZXIsIGJ5ID0gInN0b3BfbmFtZSIpDQpuYW1lcyhnYXJlc19IREZfbWVyZ2UpDQpnYXJlc19IREZfbWVyZ2Vfc2VsZWN0IDwtIGdhcmVzX0hERl9tZXJnZSAlPiUgDQogIGRwbHlyOjpzZWxlY3Qoc3RvcF9uYW1lLHZveV8yMDIyLHN1bV9wb3B1bGF0aW9uLHN1bV9saXRzLG5vbWJyZV9hcnJldHMsDQogICAgICAgICAgICAgICAgbm9tYnJlX2NvbW1lcmNlcywgbm9tYnJlX2VsZXZlcywgWkEsIHBhc3NhZ2Vfbml2ZWF1LCBzdG9wX2lkLCByb3V0ZV9pZCkNCmhlYWQoZ2FyZXNfSERGX21lcmdlX3NlbGVjdCkNCm5hbWVzKGdhcmVzX0hERl9tZXJnZV9zZWxlY3QpDQoNCm1hcHZpZXc6Om1hcHZpZXcoZ2FyZXNfSERGX21lcmdlX3NlbGVjdCkNCmBgYA0KDQpJQ0kgamUgZnVzaW9ubmUgbWVzIGRvbm7DqWVzIGF2ZWMgbGUgdGFibGVhdXggR1RGUyBkZXMgc3RvcCBuYW1lDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBGdXNpb24gZGVzIHRhYmxlYXV4IGRlIG5pdmVhdSAxIGV0IDIgLS0tLQ0KDQpnYXJlc19IREZfbWVyZ2Vfc2VsZWN0X2Z1c2lvbiA8LSBtZXJnZShnYXJlc19IREZfbWVyZ2Vfc2VsZWN0LA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgbWVyZ2VkX2RhdGEsIA0KICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgYnkgPSAncm91dGVfaWQnKQ0KaGVhZChnYXJlc19IREZfbWVyZ2Vfc2VsZWN0X2Z1c2lvbikNCm1hcHZpZXc6Om1hcHZpZXcoZ2FyZXNfSERGX21lcmdlX3NlbGVjdF9mdXNpb24pDQpgYGANCg0KSmUgZnVzaW9ubmUgbGUgdGFibGVhdSBkdSBuaXZlYXUgMSBkZXMgZ2FyZXMgKGdhcmVzX0hERl9tZXJnZV9zZWxlY3QpIGV0IGR1IG5pdmVhdSAyIGRlcyBsaWduZXMgKG1lcmdlZF9kYXRhKQ0KDQo8YnI+DQoNCiMjIyBNT0RFTEUgTVVMVElOSVZFQVVYDQoNCkplIHNvdWhhaXRlIGNvbXByZW5kcmUgbGVzIHZhcmlhYmxlcyBxdWkgaW5mbHVlbmNlbnQgbGUgbm9tYnJlIGRlIHZveWFnZXVycyBkZXMgZ2FyZXMgZW4gMjAyMi4gDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBtb2TDqGxlIG11bHRpLW5pdmVhdXggDQoNCiMgTW9kw6hsZSBkZSByw6lncmVzc2lvbiBtdWx0aW5pdmVhdXgNCm1vZGVsIDwtIGxtZTQ6OmxtZXIodm95XzIwMjIgfiBzY2FsZShzdW1fcG9wdWxhdGlvbikgKyBzY2FsZShzdW1fbGl0cykgKyBzY2FsZShub21icmVfYXJyZXRzKSArICBzY2FsZShub21icmVfY29tbWVyY2VzKSArICBzY2FsZShub21icmVfZWxldmVzKSArIHNjYWxlKFpBKSArIHNjYWxlKHBhc3NhZ2Vfbml2ZWF1KSArIHNjYWxlKGF2ZXJhZ2VfdGltZSkgKyAgc2NhbGUobnVtYmVyX29mX3N0b3BzKSArIA0KICAgICAgICAgICAgICAgICgxIHwgcm91dGVfaWQpLCAjIHByaXNlIGVuIGNvbXB0ZSBkZXMgdmFyaWFibGVzIGRlcyByb3V0ZXMgY29tbWUgcG9pbnQgZGUgZMOpcGFydCBhdmFudCBtw6ptZSBkZSBwcmVuZHJlIGVuIGNvbXB0ZSBsZXMgdmFyaWFibGVzIHN1ciBsZXMgZ2FyZXMNCiAgICAgICAgICAgICAgICBkYXRhID0gZ2FyZXNfSERGX21lcmdlX3NlbGVjdF9mdXNpb24pDQoNCiMgQWZmaWNoZXIgbGUgcsOpc3Vtw6kgZHUgbW9kw6hsZQ0Kc3VtbWFyeShtb2RlbCkNCmBgYA0KDQoNCmBgYHtyLCBvdXQud2lkdGg9JzEwMCUnfQ0KIyBSMg0KIyBJbnN0YWxsZXIgZXQgY2hhcmdlciBsZSBwYWNrYWdlIE11TUluIHNpIG7DqWNlc3NhaXJlDQppZiAoIXJlcXVpcmVOYW1lc3BhY2UoIk11TUluIiwgcXVpZXRseSA9IFRSVUUpKSBpbnN0YWxsLnBhY2thZ2VzKCJNdU1JbiIpDQpsaWJyYXJ5KE11TUluKQ0KDQojIENhbGN1bGVyIFJeMg0KcjIgPC0gci5zcXVhcmVkR0xNTShtb2RlbCkNCnByaW50KHIyKQ0KDQoNCiMgSG9tb3Njw6lkYXN0aWNpdMOpIA0KcGxvdChyZXNpZHVhbHMobW9kZWwpIH4gZml0dGVkKG1vZGVsKSkNCmFibGluZShoID0gMCwgY29sID0gInJlZCIpDQoNCiMgSGlzdG9ncmFtbWUgZGVzIHLDqXNpZHVzIHBvdXIgdsOpcmlmaWVyIGxhIG5vcm1hbGl0w6kgIA0KaGlzdChyZXNpZHVhbHMobW9kZWwpLCBicmVha3MgPSAiU2NvdHQiLCBtYWluID0gIkhpc3RvZ3JhbW1lIGRlcyBSw6lzaWR1cyIsIHhsYWIgPSAiUsOpc2lkdXMiKQ0KDQojIFFRLXBsb3QgZGVzIHLDqXNpZHVzIA0KIyBEYW5zIHVuIFFRLXBsb3QsIGxlcyBwb2ludHMgZGV2cmFpZW50IHNlIHNpdHVlciBhcHByb3hpbWF0aXZlbWVudCBsZSBsb25nIGRlIGxhIGxpZ25lIHJvdWdlIA0KIyBzaSBsZXMgcsOpc2lkdXMgc3VpdmVudCB1bmUgZGlzdHJpYnV0aW9uIG5vcm1hbGUuDQpxcW5vcm0ocmVzaWR1YWxzKG1vZGVsKSkNCnFxbGluZShyZXNpZHVhbHMobW9kZWwpLCBjb2wgPSAicmVkIikNCmBgYA0KDQojIyBUUkFOU0ZPUk1BVElPTg0KDQoqIExhICoqc3RhbmRhcmRpc2F0aW9uIChzY29yZXMgeikqKiBzZSBjb25jZW50cmUgc3VyIGxhIHJlY29uZmlndXJhdGlvbiBkZXMgZG9ubsOpZXMgcG91ciBxdSdlbGxlcyBhaWVudCB1bmUgbW95ZW5uZSBkZSAwIGV0IHVuIMOpY2FydC10eXBlIGRlIDEsIHJlbmRhbnQgYWluc2kgbGEgZGlzdHJpYnV0aW9uIGRlcyBkb25uw6llcyBzdGFuZGFyZGlzw6llIGVuIHRlcm1lcyBkJ3VuaXTDqXMgZCfDqWNhcnQtdHlwZS4gRWxsZSBlc3QgdXRpbGUgcG91ciBjb21wYXJlciBkZXMgc2NvcmVzIGVudHJlIGRpZmbDqXJlbnRlcyDDqWNoZWxsZXMgZXQgZXN0IHNvdXZlbnQgcHLDqWbDqXLDqWUgZGFucyBsZXMgYW5hbHlzZXMgcXVpIHN1cHBvc2VudCB1bmUgZGlzdHJpYnV0aW9uIG5vcm1hbGUgZGVzIGRvbm7DqWVzLiAgICANCjxicj4NCiogTGEgKipub3JtYWxpc2F0aW9uIE1pbi1NYXgqKiByZWRpbWVuc2lvbm5lIGxlcyBkb25uw6llcyBkYW5zIHVuIGludGVydmFsbGUgZml4ZSwgc291dmVudCBbMCwgMV0sIGVuIGFqdXN0YW50IGNoYXF1ZSB2YWxldXIgc2Vsb24gbGVzIHZhbGV1cnMgbWluaW1hbGVzIGV0IG1heGltYWxlcyBkZSBsJ2Vuc2VtYmxlIGRlIGRvbm7DqWVzLCBjZSBxdWkgZXN0IHV0aWxlIHBvdXIgbGVzIG1vZMOobGVzIHNlbnNpYmxlcyBhdXggdmFyaWF0aW9ucyBkJ8OpY2hlbGxlIGVudHJlIGxlcyB2YXJpYWJsZXMuIEVsbGUgZXN0IHBhcnRpY3VsacOocmVtZW50IHV0aWxlIHBvdXIgbGVzIGFsZ29yaXRobWVzIHNlbnNpYmxlcyBhdXggw6ljaGVsbGVzIGRlcyB2YXJpYWJsZXMsIGNvbW1lIGxlcyBhbGdvcml0aG1lcyBiYXPDqXMgc3VyIGxlcyBkaXN0YW5jZXMuIExhIG5vcm1hbGlzYXRpb24gTWluLU1heCBlc3Qgc291dmVudCB1dGlsaXPDqWUgZGFucyBsZXMgY29udGV4dGVzIG/DuSBsJ3VuaWZvcm1pdMOpIGRlIGwnw6ljaGVsbGUgZW50cmUgbGVzIHZhcmlhYmxlcyBlc3QgY3J1Y2lhbGUuICAgDQo8YnI+DQoqIExhICoqbm9ybWFsaXNhdGlvbiBwYXIgbGEgdmFsZXVyIG1heGltYWxlKiogYWp1c3RlIGxlcyBkb25uw6llcyBzZWxvbiBsYSBwbHVzIGdyYW5kZSB2YWxldXIgYWJzb2x1ZSBkZSBsJ2Vuc2VtYmxlIGRlIGRvbm7DqWVzLCByZW5kYW50IHRvdXRlcyBsZXMgdmFsZXVycyByZWxhdGl2ZXMgw6AgY2V0dGUgdmFsZXVyIG1heGltYWxlLCBjZSBxdWkgZXN0IHVuZSBhcHByb2NoZSBzaW1wbGlmacOpZSBkZSBtaXNlIMOgIGwnw6ljaGVsbGUgcGFyIHJhcHBvcnQgw6AgdW5lIHZhbGV1ciBkZSByw6lmw6lyZW5jZSB1bmlxdWUuIEVsbGUgZXN0IHNpbWlsYWlyZSDDoCBsYSBub3JtYWxpc2F0aW9uIE1pbi1NYXggbWFpcyBzZSBjb25jZW50cmUgdW5pcXVlbWVudCBzdXIgbGUgcmVkaW1lbnNpb25uZW1lbnQgcGFyIHJhcHBvcnQgw6AgbGEgdmFsZXVyIG1heGltYWxlIGRlIGNoYXF1ZSB2YXJpYWJsZS4gU2kgdG91dGVzIGxlcyB2YWxldXJzIHNvbnQgcG9zaXRpdmVzLCBsZXMgZG9ubsOpZXMgdmFyaWVudCBlbnRyZSAwIGV0IDEuICBMYSBub3JtYWxpc2F0aW9uIHBhciBsYSB2YWxldXIgbWF4aW1hbGUgcGV1dCDDqnRyZSBwcsOpZsOpcsOpZSBwb3VyIHNhIHNpbXBsaWNpdMOpIGV0IGxvcnNxdWUgbGEgZG9taW5hbmNlIGRlIGxhIHZhbGV1ciBtYXhpbWFsZSBlc3Qgc2lnbmlmaWNhdGl2ZSBwb3VyIGwnYW5hbHlzZS4gIA0KPGJyPg0KDQojIyBSRVNTT1VSQ0VTICANCg0KDQpNw6l0aG9kZXMgcXVhbnRpdGF0aXZlcyBlbiBzY2llbmNlcyBzb2NpYWxlcyA6IHVuIGdyYW5kIGJvbCBk4oCZUiwgQXBwYXJpY2lvIFAuIGV0IEouIEdlbGIgKDIwMjQpDQo8YSBocmVmPSJodHRwczovL3NlcmllYm9sZHIuY29tL01ldGhvZGVzUXVhbnRpdGF0aXZlcy8iIHRhcmdldD0iX2JsYW5rIj5saWVuLg0KPC9hPiAgDQoNClN1cHBvcnRzIGRlIGNvdXJzIGRlIHN0YXRpc3RpcXVlcyBzdXIgUiwgVC4gRmV1aWxsZXQNCjxhIGhyZWY9Imh0dHBzOi8vdGZldWlsbGV0LmdpdHBhZ2VzLmh1bWEtbnVtLmZyL2NvdXJzLyIgdGFyZ2V0PSJfYmxhbmsiPmxpZW4uDQo8L2E+ICANCg0KUmFwcGVsIGRlIHN0YXRpc3RpcXVlcywgTC4gUm91dmnDqHJlLCAyMDE3DQo8YSBocmVmPSJodHRwczovL2xyb3V2aWVyZS5naXRodWIuaW8vZG9jX2NvdXJzL3NsaWRlc19TSS5wZGYiIHRhcmdldD0iX2JsYW5rIj5saWVuLg0KPC9hPiAgDQoNCjwhLS0gW1JhcHBlbCBkZSBzdGF0aXN0aXF1ZXMsIEwuIFJvdXZpw6hyZSwgMjAxN10oaHR0cHM6Ly9scm91dmllcmUuZ2l0aHViLmlvL2RvY19jb3Vycy9zbGlkZXNfU0kucGRmKSAtLT4NCg0KSW50cm9kdWN0aW9uIMOgIGxhIHLDqWdyZXNzaW9uIGxpbsOpYWlyZSBtdWx0aXBsZQ0KPGEgaHJlZj0iaHR0cHM6Ly9kZWxsYWRhdGEuZnIvcmVncmVzc2lvbi1saW5lYWlyZS1tdWx0aXBsZS8iIHRhcmdldD0iX2JsYW5rIj5saWVuLg0KPC9hPiAgDQoNCjwhLS0gW0ludHJvZHVjdGlvbiDDoCBsYSByw6lncmVzc2lvbiBsaW7DqWFpcmUgbXVsdGlwbGVdKGh0dHBzOi8vZGVsbGFkYXRhLmZyL3JlZ3Jlc3Npb24tbGluZWFpcmUtbXVsdGlwbGUvKSAtLT4NCg0K